18.3.3 相似三角形的性质1[下学期]
文档属性
| 名称 | 18.3.3 相似三角形的性质1[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 451.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-08-23 00:00:00 | ||
图片预览





文档简介
课件16张PPT。四川省宜宾县育才中学校 § 18.3 相似三角形的性质教学设计课件制作:育才中学 陈伦德 § 18.3 相似三角形的性质课堂教学的过程是学生在教师指导下自学的过程教学设计课件制作:育才中学 陈伦德学习目标1, 在理解相似三角形基本性质的基础上,掌
握相似三角形对应中线、对应高线、对应角平
分线的比等于相似比,周长的比等于相似比,
面积的比等于相似比的平方。
2, 通过实践体会相似三角形的性质,会用性 质解决相关的问题。课前热身1,相似三角形有何特征?(对应边成比例,对应角相等)2,识别三角形相似的主要方法有那些?两个角对应相等的两个三角形相似。两边对应成比例且夹角相等的两个三角形相似 。三边对应成比例的两个三角形相似。自学指导 1,请同学们认真阅读P78—79,想一想云图中的问题。
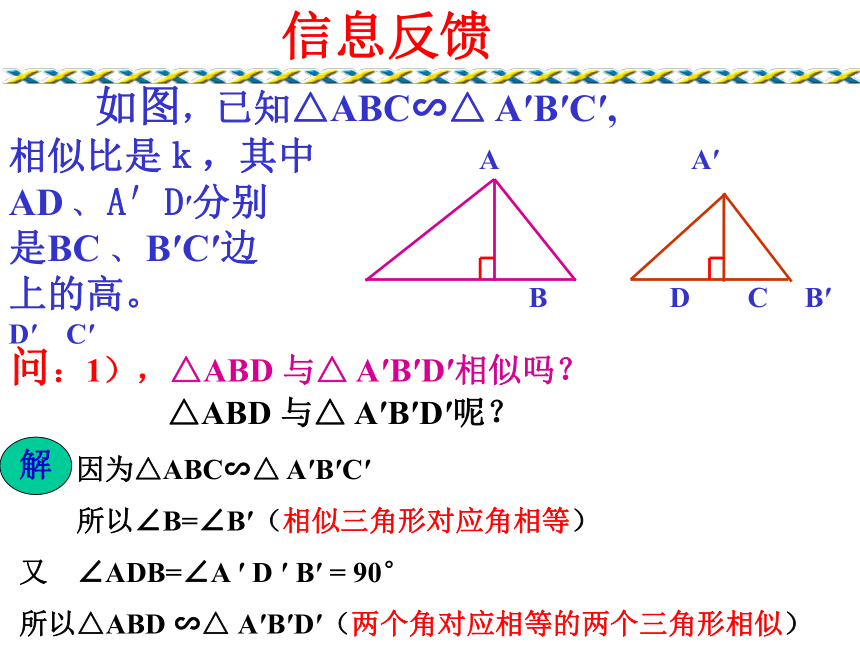
2,请同学们仿照相似三角形对应高的比等于相似比的说理过程试着写出思考中的问题。 如图,已知△ABC∽△ A′B′C′,
相似比是k,其中 A A′
AD 、 A′D′分别
是BC 、 B′C′边?
上的高。 B D C B′ D′ C′信息反馈问:1),△ABD 与△ A′B′D′相似吗? △ABD 与△ A′B′D′呢? 如图,已知△ABC∽△ A′B′C′,
相似比是k,其中 A A′
AD 、 A′D′分别
是BC 、 B′C′边?
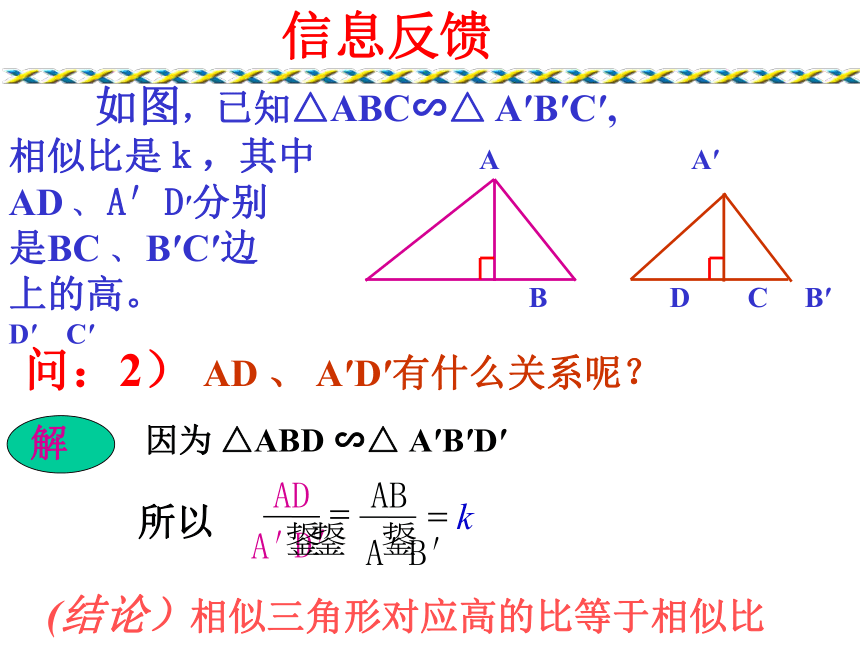
上的高。 B D C B′ D′ C′信息反馈问:2) AD 、 A′D′有什么关系呢?(结论)相似三角形对应高的比等于相似比 如图,图(1) 、 (2) 、 (3)分别是边长为
1 、 2 、 3 的等边三角形
问:1, 三个三角形彼此相似吗?为什么?
填空:
(2) 与 (1)的相似比= (2) 与 (1)的面积比=
(3) 与 (1)的相似比= (3) 与 (1)的面积比=
(3) 与 (2)的相似比= (3) 与 (2)的面积比=
问:2 ,你能发现什么吗?
(结论)相似三角形的面积比等于相似比的平方2349(1)(3)(2)试一试 如图, △ABC∽△ A′B′C′,相似比为K, AD 、 A′D′分别是BC 、 B′C′边上的中线。问:AD 、 A′D′之间有什么关系?
D'C'B'A'DCBA 因为△ABC∽△ A′B′C′
所以
解所以又又 ∠B=∠B′
所以 △ABD∽△ A′B′D′所以(结论)相似三角形对应中线的比等于相似比感悟与反思 通过前面的思考、探索、推理,我们得到相似三角形有如下性质;
相似三角形对应高的比、对应中线的比、对应角平分线的比、周长的比等于相似比。
相似三角形面积的比等于相似比的平方。例题赏析例1:如图,△ABC~△A'B'C',它们的周长分别是60厘米和72厘米,且AB=15厘米,B'C'=24厘米。求:BC、AC、A'B'、A'C'。C'B'A'CBA解:因为△ABC~△A'B'C‘
所以???又 AB=15厘米 B'C'=24厘米
所以 A'B'=18厘米 BC=20厘米 故 AC=60–15–20=25(厘米)A'C'=72–18–24=30(厘米)例题赏析例2:有同一块三角形土地的甲、乙两幅地图,比例尺分别为1:200和1:500,求甲地图与乙地图的相似比和面积比。解因为甲、乙两幅地图都与这块三角形土地相似,
所以这两幅地图相似。
设三角形土地的某一边长为m,
甲地图的对应边为a:200,乙地图的对应边为a:500,
所以这两幅地图相似比为所以 它们的面积比为25:4学习小结一,相似三角形的基本性质:
对应边比例,对应角相等
二,相似三角形的性质:
相似三角形对应高的比、对应中线的比、对应角平分线的比、周长的比等于相似比。
相似三角形面积的比等于相似比的平方。当堂训练1,P79练习题。
2,把一个三角形变成和它相似的三角形,
(1)如果边长扩大为原来的5倍,那么面积扩大为原来的————倍。
(2)如果面积扩大为原来的100倍,那么边长扩大为原来的————倍。
3,两个相似三角形的一对对应边分别是35厘米和14 厘米,
(1)它们的周长差60厘米,这两个三角形的周长分别是
——————。(2)它们的面积之和是58平方厘米,这两个三角形的面积分别是————————。2510100厘米、40厘米50平方厘米、40平方厘米当堂训练 如图,在 ABCD中,E是BC上一点,AC与DE相交于F,若AE:EB=1:2,求?AEF与?CDF的相似比。若?AEF的面积为5平方厘米,求?CDF的面积。BFEDCA挑战自我 如图,△ABC是一块锐角三角形余料,边BC=120毫米,高AD=80毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?NMQPEDCBA解:设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。设正方形PQMN的边长为x毫米。
因为PN∥BC,所以△APN∽ △ABC
所以
2, 通过实践体会相似三角形的性质,会用性 质解决相关的问题。课前热身1,相似三角形有何特征?(对应边成比例,对应角相等)2,识别三角形相似的主要方法有那些?两个角对应相等的两个三角形相似。两边对应成比例且夹角相等的两个三角形相似 。三边对应成比例的两个三角形相似。自学指导 1,请同学们认真阅读P78—79,想一想云图中的问题。
2,请同学们仿照相似三角形对应高的比等于相似比的说理过程试着写出思考中的问题。 如图,已知△ABC∽△ A′B′C′,
相似比是k,其中 A A′
AD 、 A′D′分别
是BC 、 B′C′边?
上的高。 B D C B′ D′ C′信息反馈问:1),△ABD 与△ A′B′D′相似吗? △ABD 与△ A′B′D′呢? 如图,已知△ABC∽△ A′B′C′,
相似比是k,其中 A A′
AD 、 A′D′分别
是BC 、 B′C′边?
上的高。 B D C B′ D′ C′信息反馈问:2) AD 、 A′D′有什么关系呢?(结论)相似三角形对应高的比等于相似比 如图,图(1) 、 (2) 、 (3)分别是边长为
1 、 2 、 3 的等边三角形
问:1, 三个三角形彼此相似吗?为什么?
填空:
(2) 与 (1)的相似比= (2) 与 (1)的面积比=
(3) 与 (1)的相似比= (3) 与 (1)的面积比=
(3) 与 (2)的相似比= (3) 与 (2)的面积比=
问:2 ,你能发现什么吗?
(结论)相似三角形的面积比等于相似比的平方2349(1)(3)(2)试一试 如图, △ABC∽△ A′B′C′,相似比为K, AD 、 A′D′分别是BC 、 B′C′边上的中线。问:AD 、 A′D′之间有什么关系?
D'C'B'A'DCBA 因为△ABC∽△ A′B′C′
所以
解所以又又 ∠B=∠B′
所以 △ABD∽△ A′B′D′所以(结论)相似三角形对应中线的比等于相似比感悟与反思 通过前面的思考、探索、推理,我们得到相似三角形有如下性质;
相似三角形对应高的比、对应中线的比、对应角平分线的比、周长的比等于相似比。
相似三角形面积的比等于相似比的平方。例题赏析例1:如图,△ABC~△A'B'C',它们的周长分别是60厘米和72厘米,且AB=15厘米,B'C'=24厘米。求:BC、AC、A'B'、A'C'。C'B'A'CBA解:因为△ABC~△A'B'C‘
所以???又 AB=15厘米 B'C'=24厘米
所以 A'B'=18厘米 BC=20厘米 故 AC=60–15–20=25(厘米)A'C'=72–18–24=30(厘米)例题赏析例2:有同一块三角形土地的甲、乙两幅地图,比例尺分别为1:200和1:500,求甲地图与乙地图的相似比和面积比。解因为甲、乙两幅地图都与这块三角形土地相似,
所以这两幅地图相似。
设三角形土地的某一边长为m,
甲地图的对应边为a:200,乙地图的对应边为a:500,
所以这两幅地图相似比为所以 它们的面积比为25:4学习小结一,相似三角形的基本性质:
对应边比例,对应角相等
二,相似三角形的性质:
相似三角形对应高的比、对应中线的比、对应角平分线的比、周长的比等于相似比。
相似三角形面积的比等于相似比的平方。当堂训练1,P79练习题。
2,把一个三角形变成和它相似的三角形,
(1)如果边长扩大为原来的5倍,那么面积扩大为原来的————倍。
(2)如果面积扩大为原来的100倍,那么边长扩大为原来的————倍。
3,两个相似三角形的一对对应边分别是35厘米和14 厘米,
(1)它们的周长差60厘米,这两个三角形的周长分别是
——————。(2)它们的面积之和是58平方厘米,这两个三角形的面积分别是————————。2510100厘米、40厘米50平方厘米、40平方厘米当堂训练 如图,在 ABCD中,E是BC上一点,AC与DE相交于F,若AE:EB=1:2,求?AEF与?CDF的相似比。若?AEF的面积为5平方厘米,求?CDF的面积。BFEDCA挑战自我 如图,△ABC是一块锐角三角形余料,边BC=120毫米,高AD=80毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?NMQPEDCBA解:设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。设正方形PQMN的边长为x毫米。
因为PN∥BC,所以△APN∽ △ABC
所以
