2023年初中学业水平考试数学模拟试题二(含答案)
文档属性
| 名称 | 2023年初中学业水平考试数学模拟试题二(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 947.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-03 20:31:08 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2023年 初中学业水平考试 数学模拟试题(二)
全卷满分120分 考试时间为120分
一、单项选择题(每小题2分,共12分)
1. 如图,在数轴上,手掌遮挡住的点表示的数可能是( )
( A)0.5. ( B)-0.5. ( C)-1.5. ( D)-2.5.
2.如图所示的几何体是由6个大小相同的小立方体搭成,它的主视图是( )
3.解集为x>2的不等式是( )
( A) 4x-1> 2x +5. (B)2+x<2x.
(C)-2x>- 4. (D)3x>x-4
4.如图,BD是四边形ABCD的对角线若∠1=∠2, ∠ADC= 100°, 则∠A等于( )
( A) 70° (B) 75° ( C) 80° ( D) 85°
5.如图,圆的两条弦AB, CD相交于点E,且AD= CB,∠A= 40°,则∠CEB的度数为( )
( A) 50°. ( B) 70°. ( C) 80°. ( D) 90°.
6. 雪上项目占据了2022年北京冬奥会的大部分比赛项目,有自由式滑雪、越野滑雪、跳台滑雪、无舵雪橇、有舵雪橇、高山滑雪等.如图,某滑雪运动员在坡度为5: 12的雪道上下滑65 m(坡度是指坡面的铅直高度与水平宽度的比),则该滑雪运动员沿竖直方向下降的高度为( )
(A)156m. (B)13m. (C) m. (D)25m.
二、填空题(每小题3分,共24分)
7.计算 - 的结果是
8. 若2a+3-0,则一4a一6=
9.分式 约分的结果是
10.方程组 的解是
11.如图所示的图形绕其中心至少旋转 度就可以与原图形完全重合。
12.如图是今年某月的日历表(隐去日期),表中a,b, c,d表示该方框中日期的数值,则bc-ad= 。
13. 如图,矩形ABCD的对角线AC, BD相交于点O,△OAB是等边三角形,AB=4,分别以点B, D为圆心,AO长为半径画弧,与该矩形的边相交,则图中阴影部分的面积为 (结果保留π)。
14.如图,BD是菱形ABCD的对角线,E是边AD的中点,F是边AB上的一点,将 AEF沿EF所在的直线翻折得到△A'EF,连接A'C.若AB=5,BD=6,当点A'到∠A的两边的距离相等时,A'C的长是
三、解答题(每小题5分,共20分)
15. 如图所示,AB与CD相交于点O,∠A=∠D, AO=DO,求证: AC = DB.
16. 下面是小勇解一元二次方程的过程,请认真阅读并完成相应的任务.
解: 2x2+4x-6=0
二次项系数化为1,得x2+2x-3=0,……第一步
移项,得x2+2x=3. ……第二步
配方,得x2+2x +4=3+4,即(x +2)2=7. ……第三步
由此,可得x+2=士. ……第四步
x1=2+, x2=2-. ……第五步
任务:
(1)上面小勇同学的解法中运用“配方法”将该一元二次方程化为两个一元一次方程,体现的数学思想是 (填“消元”或“降次");其中配方法依据的一个数学公式是
(2)“第二步”变形的依据是
(3) 上面小勇同学的解题过程中,从第 步开始出现错误,直接写出正确的解。
小刚所在的社区为了做好应对新冠疫情的防控工作,特招募社区抗疫志愿工作者.小刚的爸爸决定报名参加,根据规定,志愿者会被随机分到A(体温检测),B(便民代购),C(环境消杀)其中一组。
(1)求小刚的爸爸被分到C组的概率;
(2)小明的爸爸也加入了该社区的志愿者队伍,请利用画树状图或列表的方法求小明的爸爸和小刚的爸爸被分到同一组的概率。
18、 如图是4X4的正方形网格,请仅用无刻度的直尺按要求完成以下作图(保留作图痕迹).
(1)在图①中作∠ABC的角平分线;
(2)在图②中过点C作一条直线l,使点A,B到直线l的距离相等.
四、解答题(每小题7分,共28分
19.某工厂生产A,B两种型号的扫地机器人,B型机器人比A型机器人每小时的清扫面积多50%,清扫100 m2所用的时间,A型机器人比B型机器人多用40分钟,求A型号扫地机器人每小时清扫面积是多少
20. 在新冠病毒疫情期间,某校“停课不停学”,开展了网络教学。为了解八年级学生在网络学习期间英语和数学学科的学习情况,复课后从八年级学生中随机抽取60名学生进行了测试,获得了他们成绩(百分制),通过对获得数据的整理、描述和分析,得到了如下部分信息:
①英语成绩的频数分布直方图如图; (分六组: 40≤x< 50,50≤x< 60,……90≤x≤100)
②英语和数学成绩的平均数、中位数、众数如表:
学科 平均数 中位数 众数
英语 74.8 m 83
数学 72.2 70 81
③英语成绩在70≤x<80这一组的数据是:
70 71 72 73 73 73 74 76 77 77 77 78 79 79
根据以上信息,回答下列问题:
(1)表中m的值为
(2)在此次测试中,某同学的英语成绩为74分,数学成绩为71分,该同学成绩排名更靠前的学科是 (填“英语"或“数学”):理由是
(3)若该校八年级共有500名学生,请你估计英语成绩超过77分的人数.
21.为加强疫情防控工作,学校决定安装红外线体温检测仪,该设备通过探测人体红外辐射能量对进入测温区域的人员进行快速测温,无需人员停留和接触,安装说明书的部分内容如表。
问题解决:学校要求测温区域的宽度AB为4m,师生身高设定为A'A=B'B=1.7 m.即,当你进入五边形ABB'CA'内时,即可测出人体温度.请你帮助学校确定该设备的安装高度EC. (结果精确到0.1 m,参考数据: sin 34°≈0.56, cos 34°≈0.83,tan 34°≈0.67, sin28° ≈0.47, cos 28°≈0.88, tan 28°≈0.53, sin 62°≈0.88,cos62°≈0.47, tan 62°≈1. 88).
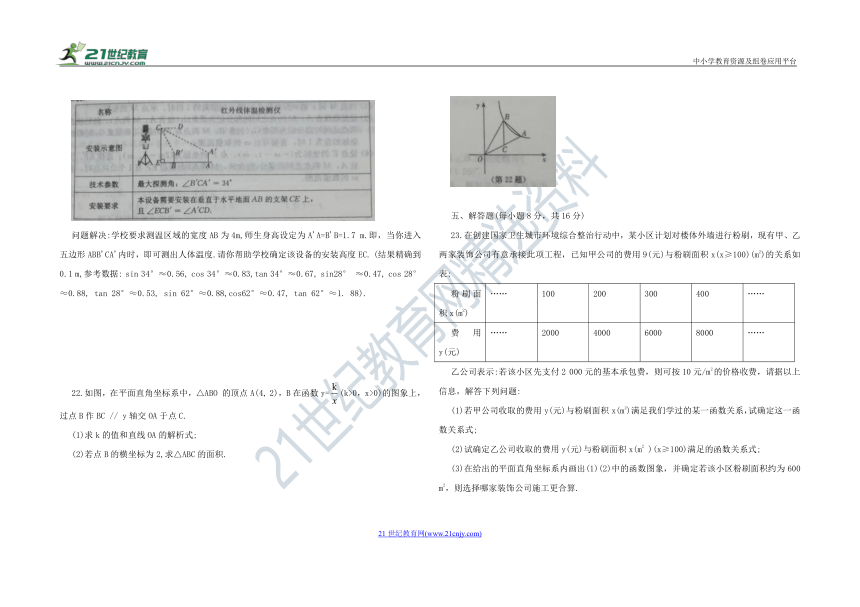
22.如图,在平面直角坐标系中,△ABO 的顶点A(4, 2),B在函数y=(k>0,x>0)的图象上,过点B作BC // y轴交OA于点C.
(1)求k的值和直线OA的解析式;
(2)若点B的横坐标为2,求△ABC的面积.
五、解答题(每小题8分,共16分)
23.在创建国家卫生城市环境综合整治行动中,某小区计划对楼体外墙进行粉刷,现有甲、乙两家装饰公司有意承接此项工程,已知甲公司的费用9(元)与粉刷面积x(x≥100)(m2)的关系如表:
粉刷面积x(m2) …… 100 200 300 400 ……
费用y(元) …… 2000 4000 6000 8000 ……
乙公司表示:若该小区先支付2 000元的基本承包费,则可按10元/m2的价格收费,请据以上信息,解答下列问题:
(1)若甲公司收取的费用y(元)与粉刷面积x(m2)满足我们学过的某一函数关系,试确定这一函数关系式;
(2)试确定乙公司收取的费用y(元)与粉刷面积x(m2 )(x≥100)满足的函数关系式;
(3)在给出的平面直角坐标系内画出(1)(2)中的函数图象,并确定若该小区粉刷面积约为600 m2,则选择哪家装饰公司施工更合算.
24.已知CD是 ABC的角平分线,点E,F分别在边AC, BC上,AD=m,BD =n,
△ADE与△BDF的面积之和为s.
(1)填空:当∠ACB=90°, DE⊥AC, DF⊥BC时,
①如图①,若∠B=45°, m=5,则n= ,S=
②如图②,若∠B=60°, m=4,则n= ,S=
(2)如图③,当∠ACB=∠EDF =90°时,探究S与m,n的数量关系,井说明理由。
六、解答题(每小题10分,共20分)
25. 如图,在矩形ABCD中,AB=8cm, BC=6 cm,动点E从点A出发以2 cm/s的速度沿射线AD方向运动,以AE为底边,在AD的右侧作等腰直角三角形AEF,当点F落在射线BC上时,点E停止运动,设△AEF与矩形ABCD重叠部分的面积为S,运动的时间为t(s).
(1)当t为何值时,点F落在射线BC上;
(2)当线段CD将 AEF的面积二等分时,求t的值;
(3)求S与t的函数关系式.
26.在平面直角坐标系中,抛物线y=x2+bx+c(b、c为常数)经过点A(0,一2)和点内B(3, 1),点M在此抛物线上,点M的横坐标为m,点M不与A, B重合.
(1)求此抛物线所对应的函数表达式;
(2)当点M到x轴的距离是点B到x轴距离的3倍时,求点M的坐标;
(3)设抛物线在A,M两点之间的部分记为图象G1(包含A, M两点),抛物线在B, M两点之间的部分记为图象G2(包含B, M两点).当图象G1和图象G2的最低点的纵坐标的差为1时,直接写出m的取值范围;
(4)设点E的坐标为(-m-1, m),点F的坐标为(2m-1, m),连接EF.当抛物线在A, M两点之间的部分(包含A, M两点)与线段EF有1个公共点时,直接写出m的取值范围.
参考答案
一、单项选择题(每小题2分,共12分)
1、B2、A3.B4.C5.C6.D
二、填空题(每小题3分,共24分)
7.
8. 0
9.-
10 .
11.120
12.48
13.Л
14.4
三、解答题(每小题5分,共20分)
15.证明:在△AOC与△DOB中,
∴△AOC≌△DOB. (4 分)
∴ AC= DB. (5分)
16. 解: (1)降次 a2士2ab +b2 = (a土b)2; (2分)
(2)等式两边同时加(减)同一个代数式,所得结果仍是等式;(3分)
(3)三. (4分)
x1 = 1, x2=-3. (5分)
17.解: (1)P(小刚的爸爸被分到C组) =(2分)
(2)根据题意,画树状图如下:
由树状图可知,共有9种等可能的结果,其中小明的爸爸和小刚的爸爸被分到同组的结果有3种,
∴P(小明的爸爸和小刚的爸爸被分到同一组)
=(5分)
18. 解: (1)如图①申,射线BP即为所求; (2分)
(2)如图②中,直线1成直线/'即为所求.(5 分)
四、解答题(每小题7分,共28分)
19. 解:若设A型扫地机器人每小时清扫x m2,则B型扫地机器人每小时清扫(1 + 50%)x m2. (1 分
解得x =50, (6 分)
经检验,x = 50是分式方程的解.(7 分)
答:设A型扫地机器人每小时清扫50 m2 .
20.解: (1) 76.5; (2分)
(2)数学; (3 分)
数学成绩大于中位数70,英语成绩低于中位数76.5; (5 分)
(3) 225(人).
答:估计该校八年级英语成绩超过77分的有225人(7 分)
21.解:如图,连接A'B'并延长,交CE于点F,则A'F 1 CE.
设CF= x.
∵∠ECB'二∠A'CD, ∠B'CA'= 34°,
∴∠FCB' =28°. (1分)
在Rt△FCB'中,FB' = tan28°·x(2分)
在Rt△FCA'中,x= tan28°. FA', (3分)
∴x = 0.53(0.53x+4). (5分)
解这个方程,x≈2.9m. (6 分)
安装高度EC≈2.9+1.7= 4.6m.
∴该设备的安装高度EC为4.6m. (7 分)
22.解: (1)∵点A(4, 2)在函数y=(k>0,x> 0)的图象上,
∴ k=4X2=8. (2分)
设直线OA的解析式为y=mx.代入点A(4, 2),
得2=4m,m=
直线OA的解析式为y=x (4分)
(2)如图,作AD⊥BC于点D,
∵B在函数,y=的图象上,点B的横坐标为2,
∴当x=2时,y=4.
∴ B(2,4)
∵直线0A的解析式为y=x,
∴当x=2时,y=1.
∴ C(2,1).
∴ BC=4-1= 3.
又∵AD-4-2= 2,
∴ S ABC =3. (7分)
五、解答题(每小题8分,共16分)
23.解:(1)由表中的数据可知甲公司收取的费用y(元)与粉刷面积x(m2)成正比例.
设y= kx.把(100,2000)代入,得2 000= 100k,
解得k= 20
所以y甲= 20x(x≥100); (2分)
(2)根据题意,得y乙 = 2000+ 10x(x≥100); (4分)
(3)画出函数的图象如图: (6 分)
把x= 600代入y甲= 20x得,
y甲= 20X600= 1 2000(元),
把x=600代入y乙= 2000 + 10x,
得y乙 =2000+ 10X 600 = 8 000(元).
y甲> y乙,
所以,确定若该小区粉刷面积约为600 m2,则选择乙装饰公司进行施工更合算。(8 分)
24.解: (1)①5 25; (2分)②4 8; (4分)
(2)如图③中,过点D作DM⊥AC于点M,DN ⊥ BC于点N.
∵DM⊥AC,DN⊥BC,CD平分∠ACB,
∴DM=DN,
∵∠DMC=∠DNC=∠MCN=90°,
∴四边形DMCN是矩形。
∵DM=DN.
∴四边形DMCN是正方形,
∴∠MDN=∠EDF = 90°.
∴∠MDE =∠NDF.
∴∠DME=∠DNF,
∴△DME≌ODNF. (6分)
∴S= S ADE+ S BDF= S ADM十S BDN.
把 BDN绕点D逆时针旋转90°得到右边 ADH,
∠ADH =90°,AD=m. DH=n,
∴S= mn. (8分)
六、解答题(每小题10分,共20分)
25.解: (1)如图①,
过点F作FH⊥AD于H.
在矩形ABCD中,
AB= 8cm. BC=6cm.∠BAD= 90°,
∵点F落在射线BC上,
∴FH=8cn.
∴ t=8s; (2分)
(2)如图②,
∵△AEF是等腰直角三角形,
∴AE边上的高线也是该边的中线。
∴点F在边CD上时,CD将△AEF的面积二等分.
∵ FD是直角三角形的斜边的直线,
∴由运动知,FD= AD=6=t.
∴t=6s; (4分)
(3)当0过点F作FH⊥AD.
由运动知,AE = 2t.
∴FH=AE=t.
∴S=AEXFH=t2 (6分)
当3过点F作FH⊥AD.
由运动知,AE=2t.
∴ DG=DE=2t-6,FH=t, DH=6-t.
∴ S= S AFH + S梯形DHFG
=-t2+12t- 18. (8分)
当6过点F作FH⊥AD.
∴DC=AD=6.
∴S=S A0G=18. (10分)
S=
26.解: (1)将点A(0,-2), 点B(3,1)代入
y=x2+bx +c,
∴
解得
∴y=x2-2x-2 (3分)
(2) ∵点M的横坐标为m,
∴ M(m, m2-2m-2).
∴ M到x 轴的距离为|m2-2m - 2|.
∵ B到x轴距离为1,
∴3=|m2-2m - 2|.
解得m=1+或m=1或m= 1.
∴ M点坐标为(1+,3)或(1-,3)或(1,-3); (6分)
(3)m<0或m=2; (8分)
提示:当y=1时,x2-2x- 2= 1.
解得x=-1或x=3.
∴ E(-1, 1).
当y=-2时,x2-2x-2=-2.
解得x=0或x=2,
∴ F(2,-2).
①如图①、图②,当m<0时,图象G1的最低点为A点,纵坐标为一2,图象G2的最低点为顶点,纵坐标为一3,
∴纵坐标的差为1.
∴ m<0时,纵坐标的差为1;
②如图③,当0∴纵坐标的差小于1:
③如图④,当1∴ m2- 2m-2+3= 1.
解得m= 2或m=0(舍).
∴ m= 2时,纵坐标的差为1;
④如图⑤,当m≥3时,图象G1的最低点为顶点,纵坐标为一3,图象G2的最低点为B点,纵坐标为1,
∴纵坐标的差大于1;
(4)m≥或-2≤m≤(10分)
提示:当m>0时,2m-1>-m- 1.
∴当M点在EF点上方时,抛物线在A, M两点之间的部分与线段EF有1个公共点.
∴m2- 2m- 2≥m.
解得m≥或m≤
∴m≥时,抛物线在A,M两点之间的部分与线段EF有1个公共点;
当m<0时,当M点在EF点上方时,A点在线段EF下方,
∴m2- 2m-2≥m,m≥- 2.
解得一2≤m≤
∴-2≤m≤
抛物线在A, M两点之间的部分与线段EF有1个公共点;
综上所述: m≥3或-2≤m≤时.抛物线在A, M两点之间的部分与线段EF有1个公共点。
21世纪教育网(www.21cnjy.com)
2023年 初中学业水平考试 数学模拟试题(二)
全卷满分120分 考试时间为120分
一、单项选择题(每小题2分,共12分)
1. 如图,在数轴上,手掌遮挡住的点表示的数可能是( )
( A)0.5. ( B)-0.5. ( C)-1.5. ( D)-2.5.
2.如图所示的几何体是由6个大小相同的小立方体搭成,它的主视图是( )
3.解集为x>2的不等式是( )
( A) 4x-1> 2x +5. (B)2+x<2x.
(C)-2x>- 4. (D)3x>x-4
4.如图,BD是四边形ABCD的对角线若∠1=∠2, ∠ADC= 100°, 则∠A等于( )
( A) 70° (B) 75° ( C) 80° ( D) 85°
5.如图,圆的两条弦AB, CD相交于点E,且AD= CB,∠A= 40°,则∠CEB的度数为( )
( A) 50°. ( B) 70°. ( C) 80°. ( D) 90°.
6. 雪上项目占据了2022年北京冬奥会的大部分比赛项目,有自由式滑雪、越野滑雪、跳台滑雪、无舵雪橇、有舵雪橇、高山滑雪等.如图,某滑雪运动员在坡度为5: 12的雪道上下滑65 m(坡度是指坡面的铅直高度与水平宽度的比),则该滑雪运动员沿竖直方向下降的高度为( )
(A)156m. (B)13m. (C) m. (D)25m.
二、填空题(每小题3分,共24分)
7.计算 - 的结果是
8. 若2a+3-0,则一4a一6=
9.分式 约分的结果是
10.方程组 的解是
11.如图所示的图形绕其中心至少旋转 度就可以与原图形完全重合。
12.如图是今年某月的日历表(隐去日期),表中a,b, c,d表示该方框中日期的数值,则bc-ad= 。
13. 如图,矩形ABCD的对角线AC, BD相交于点O,△OAB是等边三角形,AB=4,分别以点B, D为圆心,AO长为半径画弧,与该矩形的边相交,则图中阴影部分的面积为 (结果保留π)。
14.如图,BD是菱形ABCD的对角线,E是边AD的中点,F是边AB上的一点,将 AEF沿EF所在的直线翻折得到△A'EF,连接A'C.若AB=5,BD=6,当点A'到∠A的两边的距离相等时,A'C的长是
三、解答题(每小题5分,共20分)
15. 如图所示,AB与CD相交于点O,∠A=∠D, AO=DO,求证: AC = DB.
16. 下面是小勇解一元二次方程的过程,请认真阅读并完成相应的任务.
解: 2x2+4x-6=0
二次项系数化为1,得x2+2x-3=0,……第一步
移项,得x2+2x=3. ……第二步
配方,得x2+2x +4=3+4,即(x +2)2=7. ……第三步
由此,可得x+2=士. ……第四步
x1=2+, x2=2-. ……第五步
任务:
(1)上面小勇同学的解法中运用“配方法”将该一元二次方程化为两个一元一次方程,体现的数学思想是 (填“消元”或“降次");其中配方法依据的一个数学公式是
(2)“第二步”变形的依据是
(3) 上面小勇同学的解题过程中,从第 步开始出现错误,直接写出正确的解。
小刚所在的社区为了做好应对新冠疫情的防控工作,特招募社区抗疫志愿工作者.小刚的爸爸决定报名参加,根据规定,志愿者会被随机分到A(体温检测),B(便民代购),C(环境消杀)其中一组。
(1)求小刚的爸爸被分到C组的概率;
(2)小明的爸爸也加入了该社区的志愿者队伍,请利用画树状图或列表的方法求小明的爸爸和小刚的爸爸被分到同一组的概率。
18、 如图是4X4的正方形网格,请仅用无刻度的直尺按要求完成以下作图(保留作图痕迹).
(1)在图①中作∠ABC的角平分线;
(2)在图②中过点C作一条直线l,使点A,B到直线l的距离相等.
四、解答题(每小题7分,共28分
19.某工厂生产A,B两种型号的扫地机器人,B型机器人比A型机器人每小时的清扫面积多50%,清扫100 m2所用的时间,A型机器人比B型机器人多用40分钟,求A型号扫地机器人每小时清扫面积是多少
20. 在新冠病毒疫情期间,某校“停课不停学”,开展了网络教学。为了解八年级学生在网络学习期间英语和数学学科的学习情况,复课后从八年级学生中随机抽取60名学生进行了测试,获得了他们成绩(百分制),通过对获得数据的整理、描述和分析,得到了如下部分信息:
①英语成绩的频数分布直方图如图; (分六组: 40≤x< 50,50≤x< 60,……90≤x≤100)
②英语和数学成绩的平均数、中位数、众数如表:
学科 平均数 中位数 众数
英语 74.8 m 83
数学 72.2 70 81
③英语成绩在70≤x<80这一组的数据是:
70 71 72 73 73 73 74 76 77 77 77 78 79 79
根据以上信息,回答下列问题:
(1)表中m的值为
(2)在此次测试中,某同学的英语成绩为74分,数学成绩为71分,该同学成绩排名更靠前的学科是 (填“英语"或“数学”):理由是
(3)若该校八年级共有500名学生,请你估计英语成绩超过77分的人数.
21.为加强疫情防控工作,学校决定安装红外线体温检测仪,该设备通过探测人体红外辐射能量对进入测温区域的人员进行快速测温,无需人员停留和接触,安装说明书的部分内容如表。
问题解决:学校要求测温区域的宽度AB为4m,师生身高设定为A'A=B'B=1.7 m.即,当你进入五边形ABB'CA'内时,即可测出人体温度.请你帮助学校确定该设备的安装高度EC. (结果精确到0.1 m,参考数据: sin 34°≈0.56, cos 34°≈0.83,tan 34°≈0.67, sin28° ≈0.47, cos 28°≈0.88, tan 28°≈0.53, sin 62°≈0.88,cos62°≈0.47, tan 62°≈1. 88).
22.如图,在平面直角坐标系中,△ABO 的顶点A(4, 2),B在函数y=(k>0,x>0)的图象上,过点B作BC // y轴交OA于点C.
(1)求k的值和直线OA的解析式;
(2)若点B的横坐标为2,求△ABC的面积.
五、解答题(每小题8分,共16分)
23.在创建国家卫生城市环境综合整治行动中,某小区计划对楼体外墙进行粉刷,现有甲、乙两家装饰公司有意承接此项工程,已知甲公司的费用9(元)与粉刷面积x(x≥100)(m2)的关系如表:
粉刷面积x(m2) …… 100 200 300 400 ……
费用y(元) …… 2000 4000 6000 8000 ……
乙公司表示:若该小区先支付2 000元的基本承包费,则可按10元/m2的价格收费,请据以上信息,解答下列问题:
(1)若甲公司收取的费用y(元)与粉刷面积x(m2)满足我们学过的某一函数关系,试确定这一函数关系式;
(2)试确定乙公司收取的费用y(元)与粉刷面积x(m2 )(x≥100)满足的函数关系式;
(3)在给出的平面直角坐标系内画出(1)(2)中的函数图象,并确定若该小区粉刷面积约为600 m2,则选择哪家装饰公司施工更合算.
24.已知CD是 ABC的角平分线,点E,F分别在边AC, BC上,AD=m,BD =n,
△ADE与△BDF的面积之和为s.
(1)填空:当∠ACB=90°, DE⊥AC, DF⊥BC时,
①如图①,若∠B=45°, m=5,则n= ,S=
②如图②,若∠B=60°, m=4,则n= ,S=
(2)如图③,当∠ACB=∠EDF =90°时,探究S与m,n的数量关系,井说明理由。
六、解答题(每小题10分,共20分)
25. 如图,在矩形ABCD中,AB=8cm, BC=6 cm,动点E从点A出发以2 cm/s的速度沿射线AD方向运动,以AE为底边,在AD的右侧作等腰直角三角形AEF,当点F落在射线BC上时,点E停止运动,设△AEF与矩形ABCD重叠部分的面积为S,运动的时间为t(s).
(1)当t为何值时,点F落在射线BC上;
(2)当线段CD将 AEF的面积二等分时,求t的值;
(3)求S与t的函数关系式.
26.在平面直角坐标系中,抛物线y=x2+bx+c(b、c为常数)经过点A(0,一2)和点内B(3, 1),点M在此抛物线上,点M的横坐标为m,点M不与A, B重合.
(1)求此抛物线所对应的函数表达式;
(2)当点M到x轴的距离是点B到x轴距离的3倍时,求点M的坐标;
(3)设抛物线在A,M两点之间的部分记为图象G1(包含A, M两点),抛物线在B, M两点之间的部分记为图象G2(包含B, M两点).当图象G1和图象G2的最低点的纵坐标的差为1时,直接写出m的取值范围;
(4)设点E的坐标为(-m-1, m),点F的坐标为(2m-1, m),连接EF.当抛物线在A, M两点之间的部分(包含A, M两点)与线段EF有1个公共点时,直接写出m的取值范围.
参考答案
一、单项选择题(每小题2分,共12分)
1、B2、A3.B4.C5.C6.D
二、填空题(每小题3分,共24分)
7.
8. 0
9.-
10 .
11.120
12.48
13.Л
14.4
三、解答题(每小题5分,共20分)
15.证明:在△AOC与△DOB中,
∴△AOC≌△DOB. (4 分)
∴ AC= DB. (5分)
16. 解: (1)降次 a2士2ab +b2 = (a土b)2; (2分)
(2)等式两边同时加(减)同一个代数式,所得结果仍是等式;(3分)
(3)三. (4分)
x1 = 1, x2=-3. (5分)
17.解: (1)P(小刚的爸爸被分到C组) =(2分)
(2)根据题意,画树状图如下:
由树状图可知,共有9种等可能的结果,其中小明的爸爸和小刚的爸爸被分到同组的结果有3种,
∴P(小明的爸爸和小刚的爸爸被分到同一组)
=(5分)
18. 解: (1)如图①申,射线BP即为所求; (2分)
(2)如图②中,直线1成直线/'即为所求.(5 分)
四、解答题(每小题7分,共28分)
19. 解:若设A型扫地机器人每小时清扫x m2,则B型扫地机器人每小时清扫(1 + 50%)x m2. (1 分
解得x =50, (6 分)
经检验,x = 50是分式方程的解.(7 分)
答:设A型扫地机器人每小时清扫50 m2 .
20.解: (1) 76.5; (2分)
(2)数学; (3 分)
数学成绩大于中位数70,英语成绩低于中位数76.5; (5 分)
(3) 225(人).
答:估计该校八年级英语成绩超过77分的有225人(7 分)
21.解:如图,连接A'B'并延长,交CE于点F,则A'F 1 CE.
设CF= x.
∵∠ECB'二∠A'CD, ∠B'CA'= 34°,
∴∠FCB' =28°. (1分)
在Rt△FCB'中,FB' = tan28°·x(2分)
在Rt△FCA'中,x= tan28°. FA', (3分)
∴x = 0.53(0.53x+4). (5分)
解这个方程,x≈2.9m. (6 分)
安装高度EC≈2.9+1.7= 4.6m.
∴该设备的安装高度EC为4.6m. (7 分)
22.解: (1)∵点A(4, 2)在函数y=(k>0,x> 0)的图象上,
∴ k=4X2=8. (2分)
设直线OA的解析式为y=mx.代入点A(4, 2),
得2=4m,m=
直线OA的解析式为y=x (4分)
(2)如图,作AD⊥BC于点D,
∵B在函数,y=的图象上,点B的横坐标为2,
∴当x=2时,y=4.
∴ B(2,4)
∵直线0A的解析式为y=x,
∴当x=2时,y=1.
∴ C(2,1).
∴ BC=4-1= 3.
又∵AD-4-2= 2,
∴ S ABC =3. (7分)
五、解答题(每小题8分,共16分)
23.解:(1)由表中的数据可知甲公司收取的费用y(元)与粉刷面积x(m2)成正比例.
设y= kx.把(100,2000)代入,得2 000= 100k,
解得k= 20
所以y甲= 20x(x≥100); (2分)
(2)根据题意,得y乙 = 2000+ 10x(x≥100); (4分)
(3)画出函数的图象如图: (6 分)
把x= 600代入y甲= 20x得,
y甲= 20X600= 1 2000(元),
把x=600代入y乙= 2000 + 10x,
得y乙 =2000+ 10X 600 = 8 000(元).
y甲> y乙,
所以,确定若该小区粉刷面积约为600 m2,则选择乙装饰公司进行施工更合算。(8 分)
24.解: (1)①5 25; (2分)②4 8; (4分)
(2)如图③中,过点D作DM⊥AC于点M,DN ⊥ BC于点N.
∵DM⊥AC,DN⊥BC,CD平分∠ACB,
∴DM=DN,
∵∠DMC=∠DNC=∠MCN=90°,
∴四边形DMCN是矩形。
∵DM=DN.
∴四边形DMCN是正方形,
∴∠MDN=∠EDF = 90°.
∴∠MDE =∠NDF.
∴∠DME=∠DNF,
∴△DME≌ODNF. (6分)
∴S= S ADE+ S BDF= S ADM十S BDN.
把 BDN绕点D逆时针旋转90°得到右边 ADH,
∠ADH =90°,AD=m. DH=n,
∴S= mn. (8分)
六、解答题(每小题10分,共20分)
25.解: (1)如图①,
过点F作FH⊥AD于H.
在矩形ABCD中,
AB= 8cm. BC=6cm.∠BAD= 90°,
∵点F落在射线BC上,
∴FH=8cn.
∴ t=8s; (2分)
(2)如图②,
∵△AEF是等腰直角三角形,
∴AE边上的高线也是该边的中线。
∴点F在边CD上时,CD将△AEF的面积二等分.
∵ FD是直角三角形的斜边的直线,
∴由运动知,FD= AD=6=t.
∴t=6s; (4分)
(3)当0
由运动知,AE = 2t.
∴FH=AE=t.
∴S=AEXFH=t2 (6分)
当3
由运动知,AE=2t.
∴ DG=DE=2t-6,FH=t, DH=6-t.
∴ S= S AFH + S梯形DHFG
=-t2+12t- 18. (8分)
当6
∴DC=AD=6.
∴S=S A0G=18. (10分)
S=
26.解: (1)将点A(0,-2), 点B(3,1)代入
y=x2+bx +c,
∴
解得
∴y=x2-2x-2 (3分)
(2) ∵点M的横坐标为m,
∴ M(m, m2-2m-2).
∴ M到x 轴的距离为|m2-2m - 2|.
∵ B到x轴距离为1,
∴3=|m2-2m - 2|.
解得m=1+或m=1或m= 1.
∴ M点坐标为(1+,3)或(1-,3)或(1,-3); (6分)
(3)m<0或m=2; (8分)
提示:当y=1时,x2-2x- 2= 1.
解得x=-1或x=3.
∴ E(-1, 1).
当y=-2时,x2-2x-2=-2.
解得x=0或x=2,
∴ F(2,-2).
①如图①、图②,当m<0时,图象G1的最低点为A点,纵坐标为一2,图象G2的最低点为顶点,纵坐标为一3,
∴纵坐标的差为1.
∴ m<0时,纵坐标的差为1;
②如图③,当0
③如图④,当1
解得m= 2或m=0(舍).
∴ m= 2时,纵坐标的差为1;
④如图⑤,当m≥3时,图象G1的最低点为顶点,纵坐标为一3,图象G2的最低点为B点,纵坐标为1,
∴纵坐标的差大于1;
(4)m≥或-2≤m≤(10分)
提示:当m>0时,2m-1>-m- 1.
∴当M点在EF点上方时,抛物线在A, M两点之间的部分与线段EF有1个公共点.
∴m2- 2m- 2≥m.
解得m≥或m≤
∴m≥时,抛物线在A,M两点之间的部分与线段EF有1个公共点;
当m<0时,当M点在EF点上方时,A点在线段EF下方,
∴m2- 2m-2≥m,m≥- 2.
解得一2≤m≤
∴-2≤m≤
抛物线在A, M两点之间的部分与线段EF有1个公共点;
综上所述: m≥3或-2≤m≤时.抛物线在A, M两点之间的部分与线段EF有1个公共点。
21世纪教育网(www.21cnjy.com)
同课章节目录
