应用题满分必刷:圆柱和圆锥(试题)-小学数学六年级下册苏教版(含解析)
文档属性
| 名称 | 应用题满分必刷:圆柱和圆锥(试题)-小学数学六年级下册苏教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-04 11:16:38 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
应用题满分必刷:圆柱和圆锥(试题)-小学数学六年级下册苏教版
1.一个圆锥形沙堆,底面直径是8米,高1.2米。用这堆沙在10米宽的公路上铺2厘米厚的路面,能铺多少米?
2.一个长方体玻璃容器从里面量,长10厘米,宽8厘米,高15厘米。里面盛有水,水中浸没着一个高为6厘米的圆锥形铅锤,把铅锤从水中取出后水面下降了0.5厘米,这个圆锥形铅锤的底面积是多少平方厘米?
3.小米将一个圆锥形橡皮泥从顶点沿底面直径切成两半后,每个切面的面积是36平方厘米。原来这个圆锥形橡皮泥的体积是多少?
4.一个装满小麦的圆柱形粮囤,底面积是3.5平方米,高是1.8米。如果把这些小麦堆成高是1.5米的圆锥形麦堆,占地面积是多少平方米?
5.墙角堆放着一堆小麦(如图),这堆小麦的顶点在两墙角的边界线上,小麦的底面半径是2米,高为0.6米.这堆小麦的体积是多少立方米?
6.一个没有盖的圆柱形铁皮桶,底面周长是18.84分米,高是12分米,做这个水桶大约需要多少平方分米的铁皮?(用进一法保留整十数)
7.将高都是2厘米,底面半径分别是1厘米、2厘米和3厘米的3个圆柱堆在一起(如图),求这个物体的表面积。
8.压路机的滚筒是圆柱形的,它的横截面半径是0.8米,长1.7米,每滚一周能压多大面积的路面?如果转100周,压过的路面有多大?
9.一个圆柱形纸筒的底面半径是4 cm,它的侧面展开后是一个正方形,这个圆柱形纸筒的侧面积是多少平方厘米?
10.修建一个圆柱形的蓄水池,底面直径是4米,深5米。在蓄水池的四周与下底面抹上水泥,抹水泥部分的面积是多少平方米?如果每平方米用水泥0.75千克,一共需要多少千克水泥?
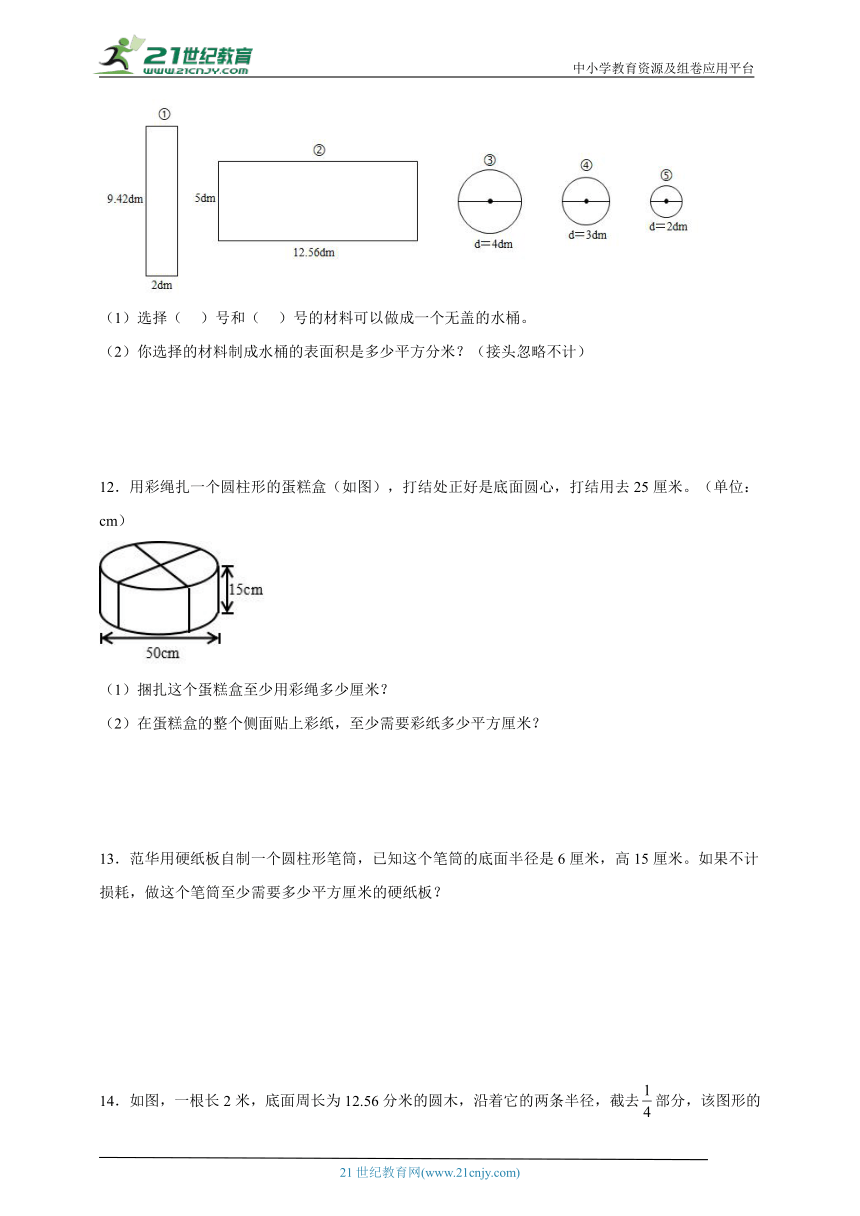
11.请你制作一个无盖的圆柱形水桶,有以下几种型号铁皮可供搭配选择。
(1)选择( )号和( )号的材料可以做成一个无盖的水桶。
(2)你选择的材料制成水桶的表面积是多少平方分米?(接头忽略不计)
12.用彩绳扎一个圆柱形的蛋糕盒(如图),打结处正好是底面圆心,打结用去25厘米。(单位:cm)
(1)捆扎这个蛋糕盒至少用彩绳多少厘米?
(2)在蛋糕盒的整个侧面贴上彩纸,至少需要彩纸多少平方厘米?
13.范华用硬纸板自制一个圆柱形笔筒,已知这个笔筒的底面半径是6厘米,高15厘米。如果不计损耗,做这个笔筒至少需要多少平方厘米的硬纸板?
14.如图,一根长2米,底面周长为12.56分米的圆木,沿着它的两条半径,截去部分,该图形的表面积是多少平方分米?
15.一个圆柱形罐头盒,高1分米,底面周长是6.28分米,罐头盒的侧面商标纸的面积最大是多少平方分米,这个罐头盒至少要用多少平方分米的铁皮?
16.一个圆柱形粮仓,它的底面积半径是1.6米,高是2米。
(1)这个粮仓是用铁皮制成的,制这个粮仓至少需要铁皮多少平方米?
(2)如果每立方米小麦重700千克,这个粮仓可装小麦多少千克?(铁皮厚度不计)
17.一个圆柱形水槽的容积是141.3立方分米,底面积是28.26平方分米,盛了的水,水的高度是多少分米?
18.一根圆柱形铁棒,底面周长是12.56厘米,长是100厘米,它的体积是多少立方厘米?
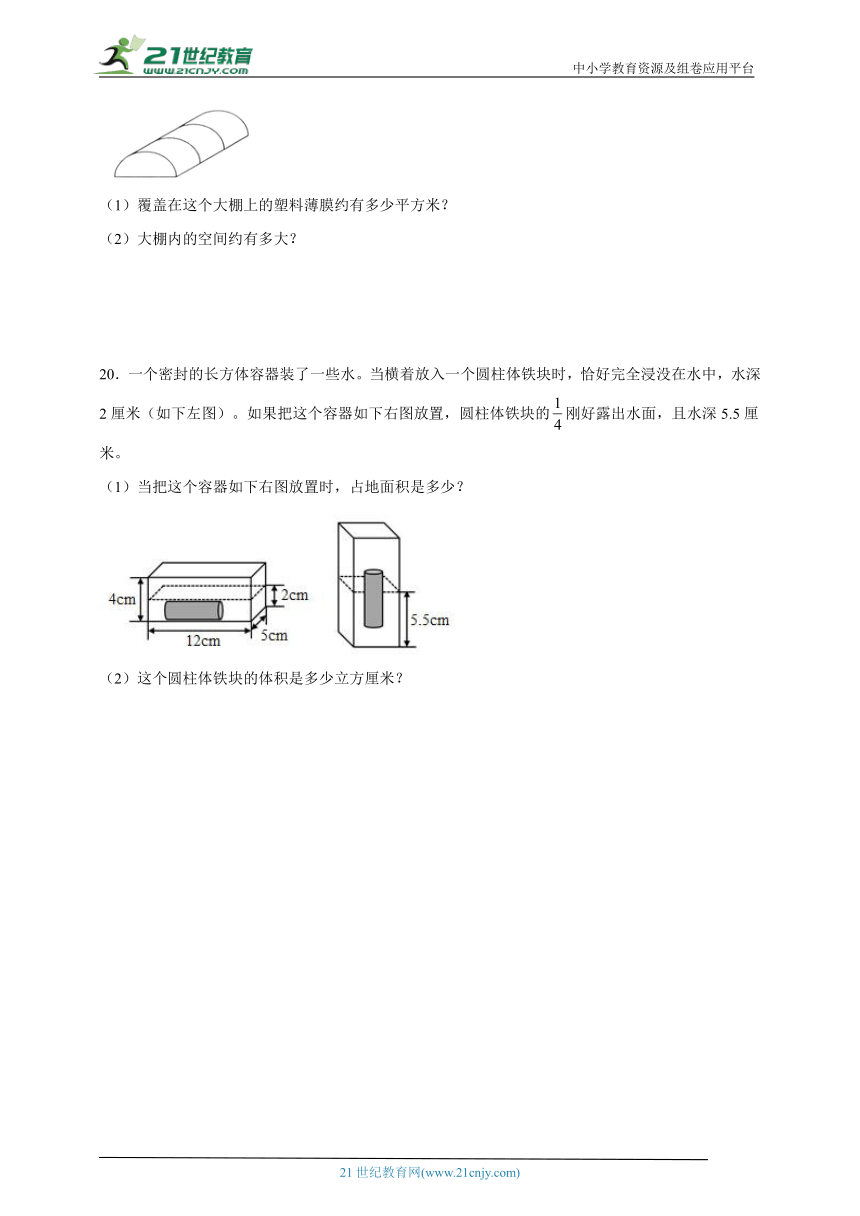
19.一个用塑料薄膜覆盖的蔬菜大棚,长20米,横截面是一个半径为2米的半圆(如下图)。
(1)覆盖在这个大棚上的塑料薄膜约有多少平方米?
(2)大棚内的空间约有多大?
20.一个密封的长方体容器装了一些水。当横着放入一个圆柱体铁块时,恰好完全浸没在水中,水深2厘米(如下左图)。如果把这个容器如下右图放置,圆柱体铁块的刚好露出水面,且水深5.5厘米。
(1)当把这个容器如下右图放置时,占地面积是多少?
(2)这个圆柱体铁块的体积是多少立方厘米?
参考答案:
1.100.48米
【分析】根据圆锥的体积公式,先求出圆锥的体积。将沙子铺在公路上后,沙子的体积没有发生变化,用沙子的体积除以公路的横截面面积,求出能铺多少米。
【详解】8÷2=4(米)
3.14×42×1.2×
=3.14×16×0.4
=20.096(立方米)
2厘米=0.02米
20.096÷(10×0.02)
=20.096÷0.2
=100.48(米)
答:能铺100.48米。
【点睛】本题考查了圆锥和长方体的体积。圆锥体积=×底面积×高,长方体体积=底面积×高。
2.20平方厘米
【分析】铅锤的体积等于容器中下降部分水的体积,根据“长方体的体积=长×宽×高”求出下降部分水的体积,再利用“”求出圆锥的底面积,据此解答。
【详解】铅锤的体积:10×8×0.5
=80×0.5
=40(立方厘米)
铅锤的底面积:40×3÷6
=120÷6
=20(平方厘米)
答:这个圆锥形铅锤的底面积是20平方厘米。
【点睛】理解容器中下降部分水的体积等于圆锥的体积是解答题目的关键。
3.226.08立方厘米
【分析】把圆锥沿底面直径把它切成两个相等的半圆锥,切面是一个三角形,这个三角形的底是圆锥的底面直径,高是圆锥的高,根据三角形的面积公式可求出圆锥的直径,进而可求出圆锥的底面积,再根据圆锥的体积公式:V=Sh求解即可。
【详解】36×2÷6
=72÷6
=12(厘米)
×3.14×(12÷2)2×6
=×3.14×36×6
=3.14×12×6
=37.68×6
=226.08(立方厘米)
答:原来这个圆锥形橡皮泥的体积是226.08立方厘米。
【点睛】本题的重点是根据圆锥的切面是一个三角形,求出圆锥的底面直径,进而根据圆锥体积的计算方法进行解答。
4.12.6平方米
【分析】根据圆柱的体积公式,V=sh,求出圆柱形粮囤里小麦的体积,再根据圆锥的体积公式,V=sh,进行变形,即可求出圆锥形麦堆的占地面积。
【详解】小麦的体积:3.5×1.8=6.3(立方米),
小麦的占地面积:6.3×3÷1.5,
=18.9÷1.5,
=12.6(平方米),
答:占地面积是12.6平方米。
【点睛】此题主要考查了圆锥和圆柱的体积公式的实际应用。
5.0.628立方米
【分析】根据“在墙角有一堆小麦,小麦顶点在两墙面交界线上”得知:这堆小麦的体积等于整堆小麦体积的.运用圆锥体积公式求出整堆小麦的体积,进而解决问题.
【详解】×3.14×22×0.6×
=×3.14×4×0.6×
=0.628(立方米)
答:这堆小麦的体积是0.628立方米.
6.260平方分米
【分析】根据圆柱的侧面积公式:s=ch,圆的面积公式:s=πr2,把数据代入公式解答即可。
【详解】18.84×12+3.14×(18.84÷3.14÷2)2,
=226.08+3.14×32,
=226.08+3.14×9,
=226.08+28.26,
=254.34,
≈260(平方分米),
答:做这个水桶大约需要260平方分米的铁皮。
【点睛】解答此题主要分清所求物体的形状,转化为求有关图形的体积或面积的问题,把实际问题转化为数学问题,再运用数学知识解决。
7.131.88平方厘米
【分析】通过平移,上边圆柱的上底面和中间圆柱上面的圆环,可以平移到最下边圆柱的上底面,组合体的表面积=最上边圆柱侧面积+中间圆柱侧面积+完整的最下面圆柱表面积,圆柱表面积=底面积×2+侧面积,圆柱侧面积=底面周长×高。
【详解】
(平方厘米)
答:这个物体的表面积是131.88平方厘米。
【点睛】关键是掌握圆柱表面积公式,具有一定的空间想象能力。
8.8.5408平方米;854.08平方米
【分析】压路机滚筒是用侧面压路,滚一周刚好是侧面积,侧面积×100=转100周的压路面积。
【详解】3.14×0.8×2×1.7=8.5408(平方米)
8.5408×100=854.08(平方米)
答:每滚一周能压8.5408平方米的路面。如果转100周,压过的路面有854.08平方米。
【点睛】本题考查了圆柱侧面积,圆柱侧面积=底面周长×高。
9.631.0144 cm2
【详解】(3.14×4×2)2=631.0144(cm2)
答:这个圆柱形纸筒的侧面积是631.0144 cm2.
10.56.52千克
【分析】计算需要抹水泥部分的面积就是求圆柱的一个底面积与侧面积的和,利用“”求出需要抹水泥部分的面积,一共需要水泥的质量=需要抹水泥部分的面积×每平方米需要水泥的质量,据此解答。
【详解】3.14×(4÷2)2+3.14×4×5
=3.14×4+3.14×4×5
=12.56+12.56×5
=12.56+62.8
=75.36(平方米)
75.36×0.75=56.52(千克)
答:一共需要56.52千克水泥。
【点睛】本题主要考查圆柱表面积公式的应用,灵活运用公式求出需要抹水泥部分的面积是解答题目的关键。
11.(1)②;③或①;④
(2)75.36平方分米或25.905平方分米
【分析】(1)根据圆柱侧面展开图的特征,圆柱的侧面沿高展开是一个长方形。这个长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高,根据圆的周长公式:C=,或C=,把数据代入公式求出三个圆的周长,然后与两个长方形的长进行比较即可。
(2)根据圆柱的侧面积公式:S=Ch,圆的面积公式:S=,把数据代入公式解答。
【详解】(1)3.14×4=12.56(分米)
3.14×3=9.42(分米)
3.14×2=6.28(分米)
所以选择的材料是②号和③号。(或者①号和④号)
(2)选择②和③的表面积:
12.56×5+3.14×(4÷2)2
=62.8+3.14×4
=62.8+12.56
=75.36(平方分米)
答:一共用了75.36平方分米的铁皮。
选择①和④的表面积:
9.42×2+3.14×(3÷2)2
=18.84+3.14×2.25
=18.84+7.065
=25.905(平方分米)
答:一共用了25.905平方分米的铁皮。
【点睛】此题考查的目的是理解掌握圆柱侧面展开图的特征及应用,圆的周长公式、圆柱的侧面积公式、圆的面积公式及应用,关键是熟记公式。
12.(1)285厘米;
(2)2355平方厘米
【分析】(1)看图可知,用的彩绳包含圆柱的4条底面直径,4条高和打结25厘米,据此列式解答即可;
(2)求彩纸面积就是求圆柱侧面积,根据圆柱侧面积=底面周长×高,列式解答即可。
【详解】(1)50×4+15×4+25
=200+60+25
=285(厘米)
答:捆扎这个蛋糕盒至少用彩绳285厘米。
(2)50×3.14×15=2355(平方厘米)
答:至少需要彩纸2355平方厘米。
【点睛】本题考查了圆柱特征和侧面积,圆柱侧面沿高展开是一个长方形,圆柱侧面积公式根据长方形面积的求法推导而来。
13.678.24平方厘米
【分析】由于笔筒无盖,所以只求这个圆柱的侧面和一个底面的总面积,根据圆柱的侧面积公式:S=,圆的面积公式:S=,把数据代入公式解答。
【详解】2×3.14×6×15+3.14×62
=6.28×6×15+3.14×36
=565.2+113.04
=678.24(平方厘米)
答:做这个笔筒至少需要678.24平方厘米的硬纸板。
【点睛】此题主要考查圆柱表面积的应用。熟记并灵活运用圆柱的侧面积公式、圆的面积公式是解题的关键。
14.287.24平方分米
【分析】由题意可知,该图形的表面积=圆柱的表面积-圆柱的表面积+两个长方形的面积即可解答。
【详解】2米=20分米
底面半径:12.56÷3.14÷2
=4÷2
=2(分米)
圆柱两个底面积之和:3.14×22×2
=12.56×2
=25.12(平方分米)
圆柱侧面积:12.56×20=251.2(平方分米)
截去后的表面积:(25.12+251.2)×(1-)
=276.32×
=207.24(dm2)
207.24+2×20×2
=207.24+80
=287.24(平方分米)
答:该图形的表面积是287.24平方分米。
【点睛】本题考查圆柱的表面积,熟记公式是解题的关键。
15.6.28平方分米,12.56平方分米
【分析】(1)盒的侧面商标纸的面积即求圆柱的侧面积,为底面周长乘以高;
(2)制作这个罐头盒所用的铁皮即求圆柱的表面积,为上下两个底面积加上侧面积.先求圆柱的半径,再根据圆柱表面积公式列式解答。
【详解】6.28×1=6.28(平方分米)
6.28÷3.14÷2=1(分米)
3.14×12×2+6.28×1
=6.28+6.28
=12.56(平方分米)
答:罐头盒的侧面商标纸的面积最大是6.28平方分米,这个罐头盒至少要用12.56平方分米的铁皮。
【点睛】本题考查了圆柱表面积和侧面积,圆柱表面积=底面积×2+侧面积。
16.(1)36.1728平方米
(2)11253.76千克
【分析】(1)求制圆柱形粮仓至少需要的铁皮,就是求圆柱的表面积;根据圆柱的表面积公式S表=S侧+2S底,其中S侧=2πrh,S底=πr2,代入数据计算即可;
(2)根据圆柱的体积公式V=πr2h,先求出这个粮仓的体积,再乘每立方米小麦的重量即可。
【详解】(1)3.14×1.6×2×2+3.14×1.62×2
=3.14×6.4+3.14×5.12
=20.096+16.0768
=36.1728(平方米)
答:制这个粮仓至少需要铁皮36.1728平方米。
(2)3.14×1.62×2
=3.14×2.56×2
=3.14×5.12
=16.0768(立方米)
16.0768×700=11253.76(千克)
答:这个粮仓可装小麦11253.76千克。
【点睛】掌握圆柱的表面积、体积计算公式是解题的关键。
17.2分米
【分析】圆柱的高=圆柱的体积÷底面积,根据分数乘法的意义,先求出水的体积,用水的体积÷底面积即可。
【详解】141.3×÷28.26
=56.52÷28.26
=2(分米)
答:水的高度是2分米。
【点睛】本题考查了分数乘法应用题和圆柱的体积公式,水盛到圆柱形水槽,其形状是圆柱形。
18.1256立方厘米
【分析】先根据圆的面积公式求出圆柱形铁棒的底面半径,再根据圆柱的体积公式V=sh求出它的体积.
【详解】12.56÷3.14÷2,
=4÷2,
=2(厘米);
3.14×22×100,
=3.14×4×100,
=3.14×400,
=1256(立方厘米).
答:它的体积是1256立方厘米.
19.(1)138.16平方米;(2)125.6立方米
【分析】(1)由题意可知,塑料薄膜的面积就是圆柱表面积的一半,即πr2+πrh,代入数据计算即可。
(2)求大棚内的空间,也就是圆柱体积的一半,即πr2h÷2,代入数据计算即可。
【详解】(1)3.14×22+3.14×2×20
=12.56+125.6
=138.16(平方米)
答:覆盖在这个大棚上的塑料薄膜约有138.16平方米。
(2)3.14×22×20÷2
=3.14×4×10
=125.6(立方米)
答:大棚内的空间约有125.6立方米。
【点睛】此题考查了圆柱表面积和体积的综合应用,明确问题所求灵活运用其计算公式解答即可。
20.(1)20平方厘米
(2)40立方厘米
【分析】(1)占地面积指的是底面积,根据长方形面积=长×宽,列式解答即可。
(2)圆柱露出水面的体积=第一个图长×宽×水深-第二个图长×宽×水深,将圆柱体积看作单位“1”,露出水面的体积÷对应分率=圆柱体积,据此列式解答。
【详解】(1)5×4=20(平方厘米)
答:占地面积是20平方厘米。
(2)12×5×2-5×4×5.5
=120-110
=10(立方厘米)
10÷=40(立方厘米)
答:这个圆柱体铁块的体积是40立方厘米。
【点睛】关键是掌握并灵活运用长方体表面积和体积公式,理解分数除法的意义。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
应用题满分必刷:圆柱和圆锥(试题)-小学数学六年级下册苏教版
1.一个圆锥形沙堆,底面直径是8米,高1.2米。用这堆沙在10米宽的公路上铺2厘米厚的路面,能铺多少米?
2.一个长方体玻璃容器从里面量,长10厘米,宽8厘米,高15厘米。里面盛有水,水中浸没着一个高为6厘米的圆锥形铅锤,把铅锤从水中取出后水面下降了0.5厘米,这个圆锥形铅锤的底面积是多少平方厘米?
3.小米将一个圆锥形橡皮泥从顶点沿底面直径切成两半后,每个切面的面积是36平方厘米。原来这个圆锥形橡皮泥的体积是多少?
4.一个装满小麦的圆柱形粮囤,底面积是3.5平方米,高是1.8米。如果把这些小麦堆成高是1.5米的圆锥形麦堆,占地面积是多少平方米?
5.墙角堆放着一堆小麦(如图),这堆小麦的顶点在两墙角的边界线上,小麦的底面半径是2米,高为0.6米.这堆小麦的体积是多少立方米?
6.一个没有盖的圆柱形铁皮桶,底面周长是18.84分米,高是12分米,做这个水桶大约需要多少平方分米的铁皮?(用进一法保留整十数)
7.将高都是2厘米,底面半径分别是1厘米、2厘米和3厘米的3个圆柱堆在一起(如图),求这个物体的表面积。
8.压路机的滚筒是圆柱形的,它的横截面半径是0.8米,长1.7米,每滚一周能压多大面积的路面?如果转100周,压过的路面有多大?
9.一个圆柱形纸筒的底面半径是4 cm,它的侧面展开后是一个正方形,这个圆柱形纸筒的侧面积是多少平方厘米?
10.修建一个圆柱形的蓄水池,底面直径是4米,深5米。在蓄水池的四周与下底面抹上水泥,抹水泥部分的面积是多少平方米?如果每平方米用水泥0.75千克,一共需要多少千克水泥?
11.请你制作一个无盖的圆柱形水桶,有以下几种型号铁皮可供搭配选择。
(1)选择( )号和( )号的材料可以做成一个无盖的水桶。
(2)你选择的材料制成水桶的表面积是多少平方分米?(接头忽略不计)
12.用彩绳扎一个圆柱形的蛋糕盒(如图),打结处正好是底面圆心,打结用去25厘米。(单位:cm)
(1)捆扎这个蛋糕盒至少用彩绳多少厘米?
(2)在蛋糕盒的整个侧面贴上彩纸,至少需要彩纸多少平方厘米?
13.范华用硬纸板自制一个圆柱形笔筒,已知这个笔筒的底面半径是6厘米,高15厘米。如果不计损耗,做这个笔筒至少需要多少平方厘米的硬纸板?
14.如图,一根长2米,底面周长为12.56分米的圆木,沿着它的两条半径,截去部分,该图形的表面积是多少平方分米?
15.一个圆柱形罐头盒,高1分米,底面周长是6.28分米,罐头盒的侧面商标纸的面积最大是多少平方分米,这个罐头盒至少要用多少平方分米的铁皮?
16.一个圆柱形粮仓,它的底面积半径是1.6米,高是2米。
(1)这个粮仓是用铁皮制成的,制这个粮仓至少需要铁皮多少平方米?
(2)如果每立方米小麦重700千克,这个粮仓可装小麦多少千克?(铁皮厚度不计)
17.一个圆柱形水槽的容积是141.3立方分米,底面积是28.26平方分米,盛了的水,水的高度是多少分米?
18.一根圆柱形铁棒,底面周长是12.56厘米,长是100厘米,它的体积是多少立方厘米?
19.一个用塑料薄膜覆盖的蔬菜大棚,长20米,横截面是一个半径为2米的半圆(如下图)。
(1)覆盖在这个大棚上的塑料薄膜约有多少平方米?
(2)大棚内的空间约有多大?
20.一个密封的长方体容器装了一些水。当横着放入一个圆柱体铁块时,恰好完全浸没在水中,水深2厘米(如下左图)。如果把这个容器如下右图放置,圆柱体铁块的刚好露出水面,且水深5.5厘米。
(1)当把这个容器如下右图放置时,占地面积是多少?
(2)这个圆柱体铁块的体积是多少立方厘米?
参考答案:
1.100.48米
【分析】根据圆锥的体积公式,先求出圆锥的体积。将沙子铺在公路上后,沙子的体积没有发生变化,用沙子的体积除以公路的横截面面积,求出能铺多少米。
【详解】8÷2=4(米)
3.14×42×1.2×
=3.14×16×0.4
=20.096(立方米)
2厘米=0.02米
20.096÷(10×0.02)
=20.096÷0.2
=100.48(米)
答:能铺100.48米。
【点睛】本题考查了圆锥和长方体的体积。圆锥体积=×底面积×高,长方体体积=底面积×高。
2.20平方厘米
【分析】铅锤的体积等于容器中下降部分水的体积,根据“长方体的体积=长×宽×高”求出下降部分水的体积,再利用“”求出圆锥的底面积,据此解答。
【详解】铅锤的体积:10×8×0.5
=80×0.5
=40(立方厘米)
铅锤的底面积:40×3÷6
=120÷6
=20(平方厘米)
答:这个圆锥形铅锤的底面积是20平方厘米。
【点睛】理解容器中下降部分水的体积等于圆锥的体积是解答题目的关键。
3.226.08立方厘米
【分析】把圆锥沿底面直径把它切成两个相等的半圆锥,切面是一个三角形,这个三角形的底是圆锥的底面直径,高是圆锥的高,根据三角形的面积公式可求出圆锥的直径,进而可求出圆锥的底面积,再根据圆锥的体积公式:V=Sh求解即可。
【详解】36×2÷6
=72÷6
=12(厘米)
×3.14×(12÷2)2×6
=×3.14×36×6
=3.14×12×6
=37.68×6
=226.08(立方厘米)
答:原来这个圆锥形橡皮泥的体积是226.08立方厘米。
【点睛】本题的重点是根据圆锥的切面是一个三角形,求出圆锥的底面直径,进而根据圆锥体积的计算方法进行解答。
4.12.6平方米
【分析】根据圆柱的体积公式,V=sh,求出圆柱形粮囤里小麦的体积,再根据圆锥的体积公式,V=sh,进行变形,即可求出圆锥形麦堆的占地面积。
【详解】小麦的体积:3.5×1.8=6.3(立方米),
小麦的占地面积:6.3×3÷1.5,
=18.9÷1.5,
=12.6(平方米),
答:占地面积是12.6平方米。
【点睛】此题主要考查了圆锥和圆柱的体积公式的实际应用。
5.0.628立方米
【分析】根据“在墙角有一堆小麦,小麦顶点在两墙面交界线上”得知:这堆小麦的体积等于整堆小麦体积的.运用圆锥体积公式求出整堆小麦的体积,进而解决问题.
【详解】×3.14×22×0.6×
=×3.14×4×0.6×
=0.628(立方米)
答:这堆小麦的体积是0.628立方米.
6.260平方分米
【分析】根据圆柱的侧面积公式:s=ch,圆的面积公式:s=πr2,把数据代入公式解答即可。
【详解】18.84×12+3.14×(18.84÷3.14÷2)2,
=226.08+3.14×32,
=226.08+3.14×9,
=226.08+28.26,
=254.34,
≈260(平方分米),
答:做这个水桶大约需要260平方分米的铁皮。
【点睛】解答此题主要分清所求物体的形状,转化为求有关图形的体积或面积的问题,把实际问题转化为数学问题,再运用数学知识解决。
7.131.88平方厘米
【分析】通过平移,上边圆柱的上底面和中间圆柱上面的圆环,可以平移到最下边圆柱的上底面,组合体的表面积=最上边圆柱侧面积+中间圆柱侧面积+完整的最下面圆柱表面积,圆柱表面积=底面积×2+侧面积,圆柱侧面积=底面周长×高。
【详解】
(平方厘米)
答:这个物体的表面积是131.88平方厘米。
【点睛】关键是掌握圆柱表面积公式,具有一定的空间想象能力。
8.8.5408平方米;854.08平方米
【分析】压路机滚筒是用侧面压路,滚一周刚好是侧面积,侧面积×100=转100周的压路面积。
【详解】3.14×0.8×2×1.7=8.5408(平方米)
8.5408×100=854.08(平方米)
答:每滚一周能压8.5408平方米的路面。如果转100周,压过的路面有854.08平方米。
【点睛】本题考查了圆柱侧面积,圆柱侧面积=底面周长×高。
9.631.0144 cm2
【详解】(3.14×4×2)2=631.0144(cm2)
答:这个圆柱形纸筒的侧面积是631.0144 cm2.
10.56.52千克
【分析】计算需要抹水泥部分的面积就是求圆柱的一个底面积与侧面积的和,利用“”求出需要抹水泥部分的面积,一共需要水泥的质量=需要抹水泥部分的面积×每平方米需要水泥的质量,据此解答。
【详解】3.14×(4÷2)2+3.14×4×5
=3.14×4+3.14×4×5
=12.56+12.56×5
=12.56+62.8
=75.36(平方米)
75.36×0.75=56.52(千克)
答:一共需要56.52千克水泥。
【点睛】本题主要考查圆柱表面积公式的应用,灵活运用公式求出需要抹水泥部分的面积是解答题目的关键。
11.(1)②;③或①;④
(2)75.36平方分米或25.905平方分米
【分析】(1)根据圆柱侧面展开图的特征,圆柱的侧面沿高展开是一个长方形。这个长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高,根据圆的周长公式:C=,或C=,把数据代入公式求出三个圆的周长,然后与两个长方形的长进行比较即可。
(2)根据圆柱的侧面积公式:S=Ch,圆的面积公式:S=,把数据代入公式解答。
【详解】(1)3.14×4=12.56(分米)
3.14×3=9.42(分米)
3.14×2=6.28(分米)
所以选择的材料是②号和③号。(或者①号和④号)
(2)选择②和③的表面积:
12.56×5+3.14×(4÷2)2
=62.8+3.14×4
=62.8+12.56
=75.36(平方分米)
答:一共用了75.36平方分米的铁皮。
选择①和④的表面积:
9.42×2+3.14×(3÷2)2
=18.84+3.14×2.25
=18.84+7.065
=25.905(平方分米)
答:一共用了25.905平方分米的铁皮。
【点睛】此题考查的目的是理解掌握圆柱侧面展开图的特征及应用,圆的周长公式、圆柱的侧面积公式、圆的面积公式及应用,关键是熟记公式。
12.(1)285厘米;
(2)2355平方厘米
【分析】(1)看图可知,用的彩绳包含圆柱的4条底面直径,4条高和打结25厘米,据此列式解答即可;
(2)求彩纸面积就是求圆柱侧面积,根据圆柱侧面积=底面周长×高,列式解答即可。
【详解】(1)50×4+15×4+25
=200+60+25
=285(厘米)
答:捆扎这个蛋糕盒至少用彩绳285厘米。
(2)50×3.14×15=2355(平方厘米)
答:至少需要彩纸2355平方厘米。
【点睛】本题考查了圆柱特征和侧面积,圆柱侧面沿高展开是一个长方形,圆柱侧面积公式根据长方形面积的求法推导而来。
13.678.24平方厘米
【分析】由于笔筒无盖,所以只求这个圆柱的侧面和一个底面的总面积,根据圆柱的侧面积公式:S=,圆的面积公式:S=,把数据代入公式解答。
【详解】2×3.14×6×15+3.14×62
=6.28×6×15+3.14×36
=565.2+113.04
=678.24(平方厘米)
答:做这个笔筒至少需要678.24平方厘米的硬纸板。
【点睛】此题主要考查圆柱表面积的应用。熟记并灵活运用圆柱的侧面积公式、圆的面积公式是解题的关键。
14.287.24平方分米
【分析】由题意可知,该图形的表面积=圆柱的表面积-圆柱的表面积+两个长方形的面积即可解答。
【详解】2米=20分米
底面半径:12.56÷3.14÷2
=4÷2
=2(分米)
圆柱两个底面积之和:3.14×22×2
=12.56×2
=25.12(平方分米)
圆柱侧面积:12.56×20=251.2(平方分米)
截去后的表面积:(25.12+251.2)×(1-)
=276.32×
=207.24(dm2)
207.24+2×20×2
=207.24+80
=287.24(平方分米)
答:该图形的表面积是287.24平方分米。
【点睛】本题考查圆柱的表面积,熟记公式是解题的关键。
15.6.28平方分米,12.56平方分米
【分析】(1)盒的侧面商标纸的面积即求圆柱的侧面积,为底面周长乘以高;
(2)制作这个罐头盒所用的铁皮即求圆柱的表面积,为上下两个底面积加上侧面积.先求圆柱的半径,再根据圆柱表面积公式列式解答。
【详解】6.28×1=6.28(平方分米)
6.28÷3.14÷2=1(分米)
3.14×12×2+6.28×1
=6.28+6.28
=12.56(平方分米)
答:罐头盒的侧面商标纸的面积最大是6.28平方分米,这个罐头盒至少要用12.56平方分米的铁皮。
【点睛】本题考查了圆柱表面积和侧面积,圆柱表面积=底面积×2+侧面积。
16.(1)36.1728平方米
(2)11253.76千克
【分析】(1)求制圆柱形粮仓至少需要的铁皮,就是求圆柱的表面积;根据圆柱的表面积公式S表=S侧+2S底,其中S侧=2πrh,S底=πr2,代入数据计算即可;
(2)根据圆柱的体积公式V=πr2h,先求出这个粮仓的体积,再乘每立方米小麦的重量即可。
【详解】(1)3.14×1.6×2×2+3.14×1.62×2
=3.14×6.4+3.14×5.12
=20.096+16.0768
=36.1728(平方米)
答:制这个粮仓至少需要铁皮36.1728平方米。
(2)3.14×1.62×2
=3.14×2.56×2
=3.14×5.12
=16.0768(立方米)
16.0768×700=11253.76(千克)
答:这个粮仓可装小麦11253.76千克。
【点睛】掌握圆柱的表面积、体积计算公式是解题的关键。
17.2分米
【分析】圆柱的高=圆柱的体积÷底面积,根据分数乘法的意义,先求出水的体积,用水的体积÷底面积即可。
【详解】141.3×÷28.26
=56.52÷28.26
=2(分米)
答:水的高度是2分米。
【点睛】本题考查了分数乘法应用题和圆柱的体积公式,水盛到圆柱形水槽,其形状是圆柱形。
18.1256立方厘米
【分析】先根据圆的面积公式求出圆柱形铁棒的底面半径,再根据圆柱的体积公式V=sh求出它的体积.
【详解】12.56÷3.14÷2,
=4÷2,
=2(厘米);
3.14×22×100,
=3.14×4×100,
=3.14×400,
=1256(立方厘米).
答:它的体积是1256立方厘米.
19.(1)138.16平方米;(2)125.6立方米
【分析】(1)由题意可知,塑料薄膜的面积就是圆柱表面积的一半,即πr2+πrh,代入数据计算即可。
(2)求大棚内的空间,也就是圆柱体积的一半,即πr2h÷2,代入数据计算即可。
【详解】(1)3.14×22+3.14×2×20
=12.56+125.6
=138.16(平方米)
答:覆盖在这个大棚上的塑料薄膜约有138.16平方米。
(2)3.14×22×20÷2
=3.14×4×10
=125.6(立方米)
答:大棚内的空间约有125.6立方米。
【点睛】此题考查了圆柱表面积和体积的综合应用,明确问题所求灵活运用其计算公式解答即可。
20.(1)20平方厘米
(2)40立方厘米
【分析】(1)占地面积指的是底面积,根据长方形面积=长×宽,列式解答即可。
(2)圆柱露出水面的体积=第一个图长×宽×水深-第二个图长×宽×水深,将圆柱体积看作单位“1”,露出水面的体积÷对应分率=圆柱体积,据此列式解答。
【详解】(1)5×4=20(平方厘米)
答:占地面积是20平方厘米。
(2)12×5×2-5×4×5.5
=120-110
=10(立方厘米)
10÷=40(立方厘米)
答:这个圆柱体铁块的体积是40立方厘米。
【点睛】关键是掌握并灵活运用长方体表面积和体积公式,理解分数除法的意义。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
