苏教版五年级下册第六单元质量调研卷(含答案+详细解析)
文档属性
| 名称 | 苏教版五年级下册第六单元质量调研卷(含答案+详细解析) |  | |
| 格式 | doc | ||
| 文件大小 | 647.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-04 15:31:28 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
苏教版小学数学
五年级下册第六单元质量调研卷
一、选择题(16分)
1.把一些鸡和兔放在同一只笼子里,从上面数有30个头,从下面数有64条腿。那么鸡比兔子多( )只。
A.15 B.20 C.26 D.28
2.根据规律算一算。
……
( )
A. B. C. D.
3.下图是由一个大正方形与一个小正方形拼成的,已知小正方形的边长为4cm,阴影部分的面积为28cm2。那么空白部分的面积为( )cm2。
A.20 B.24 C.28 D.32
4.观察下列式子:0.2=123÷999,0.3=237÷999,0.4=45÷999,那么,0.5等于( )。
A.0.45÷999 B.4.5÷999 C.45÷999 D.450÷999
5.把一根10米长的细绳分别围成以下三个图形,( )的面积最小。
A.长方形 B.正方形 C.圆 D.无法判断
6.根据37037×3=111111,37037×6=222222,37037×9=333333,那么37037×18=( )。
A.444444 B.555555 C.666666 D.999999
7.兴趣小组正在探索求下图组合图形的面积,其中( )的方法是错误的。
A.淘气:把图形分割成一个梯形和一个长方形,再求各部分面积的和
B.笑笑:把图形分割成一个三角形和一个梯形,再求各部分面积的和
C.奇思:把图形看成一个长方形,用其面积减去一个梯形的面积
D.妙想:把线绕图形围一周,再把这条线围成一个正方形,求正方形的面积
8.观察下面的算式:5×9=45
55×99=5445
555×999=554445
5555×9999=55544445
则5555555555×9999999999=( )。
A.5555555554444444445 B.5555555555444444444445
C.55555555544444444445
二、填空题(42分)
9.一头猪能换三只羊,一头牛能换六头猪,一头牛可以换_______只羊。
10.如图中阴影部分面积是21平方厘米,那么大三角形的面积是________平方厘米。
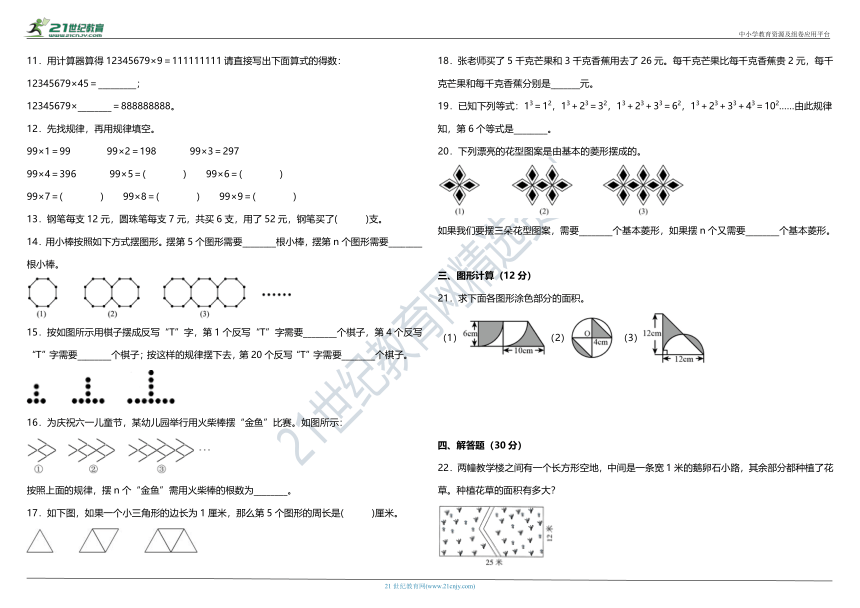
11.用计算器算得12345679×9=111111111请直接写出下面算式的得数:
12345679×45=_________;
12345679×________=888888888。
12.先找规律,再用规律填空。
99×1=99 99×2=198 99×3=297
99×4=396 99×5=( ) 99×6=( )
99×7=( ) 99×8=( ) 99×9=( )
13.钢笔每支12元,圆珠笔每支7元,共买6支,用了52元,钢笔买了( )支。
14.用小棒按照如下方式摆图形。摆第5个图形需要________根小棒,摆第n个图形需要________根小棒。
15.按如图所示用棋子摆成反写“T”字,第1个反写“T”字需要________个棋子,第4个反写“T”字需要________个棋子;按这样的规律摆下去,第20个反写“T”字需要________个棋子。
16.为庆祝六一儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛。如图所示:
按照上面的规律,摆n个“金鱼”需用火柴棒的根数为________。
17.如下图,如果一个小三角形的边长为1厘米,那么第5个图形的周长是( )厘米。
18.张老师买了5千克芒果和3千克香蕉用去了26元。每千克芒果比每千克香蕉贵2元,每千克芒果和每千克香蕉分别是_______元。
19.已知下列等式:13=12,13+23=32,13+23+33=62,13+23+33+43=102……由此规律知,第6个等式是________。
20.下列漂亮的花型图案是由基本的菱形摆成的。
如果我们要摆三朵花型图案,需要________个基本菱形,如果摆n个又需要________个基本菱形。
三、图形计算(12分)
21.求下面各图形涂色部分的面积。
(1)(2) (3)
四、解答题(30分)
22.两幢教学楼之间有一个长方形空地,中间是一条宽1米的鹅卵石小路,其余部分都种植了花草。种植花草的面积有多大?
23.观察下面的等式和相应的图形(每一个正方形的边长均为1),探究其中的规律:
①1×=1-←→
②2×=2-←→
③3×=3-←→
④4×=4-←→
(1)写出第5个等式,并在下面给出的5个正方形上画出与之对应的图形。
________←→
(2)猜想并写出与第100个图形相对应的等式。
24.解放路实验学校报告厅共有25排座位。其中第一排有10个座位,第二排有12个座位,后面每一排的座位都比前一排多2个。解放路实验学校的报告厅一共有多少个座位?
25.“海象杯”少儿围棋赛共有32名选手参加,比赛采用单场淘汰制,要决出冠军,共要比赛多少场?如果有64名选手参加比赛,产生冠军共要比赛多少场?
26.一块长80米、宽50米的长方形绿化带,中间有两条宽1米的小路,其余地方为草坪。草坪的面积是多少平方米?
27.王老师买了2支钢笔和6支圆珠笔,共付60元,已知1支钢笔的价钱和3支圆珠笔的价钱一样多,每支钢笔和每支圆珠笔各多少元?
28.从2开始,连续的偶数相加,它们和的情况如下:
2=1×2
2+4=6=2×3
2+4+6=12=3×4
2+4+6+8=20=4×5
2+4+6+8+10=30=5×6
……
(1)根据表中的规律猜想,用n的式子表示s的公式为S=2+4+6+8+…+2n=_____。
(2)根据上题的规律计算①2+4+6+8+…+28
②104+106+108+…+200
29.
(1)2张桌子拼在一起可坐多少人?4张桌子呢?n张桌子呢?(n为非0自然数)
(2)一家餐厅有40张这样的长方形桌子,按照上图方式每5张拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐________人。
(3)在(2)题中,若改成每8张桌子拼成1张大桌子,则共可坐________人。
参考答案:
1.C
【分析】从题中可知鸡兔共有30只,假设30只都是兔子,则会有腿4×30=120(条)比实际多出了120-64=56(条),一只兔子比一只鸡多两条腿,则鸡的只数就是:56÷(4-2)=28(只),兔子只数是30-28=2(只),从而也可求出鸡比兔子多的只数。
【详解】假设30只动物都是兔子,则鸡的只数:
(4×30-64)÷(4-2)
=56÷2=28(只)
30-28=2(只)
28-2=26(只)
答:鸡比兔子多26只。
故答案为:C。
【点睛】解这类题的关键是用假设法进行分析,进而得出结论,也可以用方程进行解答。
2.D
【解析】从所给算式可以看出:算式等号左边都是连续的偶数,右边的结果为:偶数的个数×(个数+1),即n×(n+1),据此解答。
【详解】由分析可得,10×(10+1)=10×11;
故答案为:D
【点睛】观察特例特点,找出规律,根据规律进行解答。
3.B
【分析】阴影部分是由一个三角形和小正方形组成的。正方形的面积=边长×边长,据此可以求出小正方形的面积。用阴影部分的面积减去小正方形的面积即是三角形的面积,三角形的高是4厘米,根据三角形的面积=底×高÷2,可以求出三角形的底,即是大正方形的边长。求出大正方形的面积,再减去三角形的面积就是空白部分的面积。
【详解】28-4×4=12(平方厘米)
12×2÷4=6(厘米)
6×6-12=24(平方厘米)
故答案为:B
【点睛】用阴影部分的面积减去小正方形的面积求出三角形的面积,继而求出三角形的底是解题的关键。
4.D
【分析】观察已知三个算式,当除数是999时,将被除数小数点向左移动3位,然后在十分位和千分位的数字上加上循环符号,就是算式的商,据此反推。
【详解】观察已知三个算式,当除数是999时,将被除数小数点向左移动3位,然后在十分位和千分位的数字上加上循环符号,就是算式的商,
所以,已知商为0.5,将循环符号去掉,然后小数点向右移动三位就是被除数,即450,得到算式:0.5=450÷999
故选:D。
【点睛】本题主要考查了“式”的规律,发现已知算式商和被除数之间的关系,是本题解题的关键。
5.A
【分析】已知三个图形的周长,可以根据圆的周长公式可得r=C÷π÷2,再根据圆的面积公式S=πr2,求出圆的面积;根据正方形的周长公式可得a=C÷4,求出正方形的边长,再根据正方形的面积=a2,求出正方形的面积;周长一定,也就是长方形长与宽的和一定,当长与宽越接近时面积越大,当长与宽相等时面积最大,此时是正方形,也就是正方形的面积大于长方形的面,再比较求出圆的面积和正方形的面积即可得出结论。
【详解】(1)圆的半径:10÷3.14÷2≈1.6(米);
则圆的面积为:3.14×1.62=8.0384(平方米)
(2)正方形的面积:正方形的边长为10÷4=2.5(米)
正方形面积为:2.5×2.5=6.25(平方米)
(3)而周长一定时正方形的面积比长方形的面积大
8.0384>6.25,
由以上计算可以得出,当周长一定时,圆的面积最大,长方形的面积最小。
故答案选:A
【点睛】解决本题要明确:周长相等的平面图形中,圆的面积最大;以及两个数的和一定,这两个数越接近时乘积越大。
6.C
【分析】根据积的变化规律:一个因数不变,另一个因数扩大到原来的多少倍(0除外),积也扩大到原来的多少倍,据此解答即可。
【详解】37037×3=111111
37037×6=222222
37037×9=333333
那么37037×18=666666
故本题答案为:C。
【点评】通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力。
7.D
【分析】根据组合图形面积的意义逐项分析。
【详解】A.如图所示:,把图形分割成一个梯形和一个长方形,再求各部分面积的和即是组合图形的面积,此方法正确;
B.如图所示:,把图形分割成一个三角形和一个梯形,再求各部分面积的和即是组合图形的面积,此方法正确;
C.如图所示:,把图形看成一个长方形,用其面积减去一个梯形的面积即是组合图形的面积,此方法正确;
D.把线绕图形围一周,再把这条线围成一个正方形,这个正方形和这个组合图形的周长相等,但面积不一定相等,此方法错误。
故答案为:D
【点睛】本题考查组合图形的面积,一般用“分割法”或“添补法”解答。
8.C
【分析】通过观察,55×99=5445,555×999=554445,5555×9999=55544445,得出规律:各位数字都是5和各位数字都是9的n位数相乘,结果中前n﹣1位数字是5,接着n位数字是4,个位数字是5;当n=10时,代入,即可得解。
【详解】55×99=5445
555×999=554445
5555×9999=55544445;
555555555×999999999=55555555544444444445;
故答案为:C。
【点睛】认真分析,找出算式中的规律,是解决此题的关键。
9.18
【分析】一头牛能换六头猪,一头猪能换三只羊,根据乘法的意义可知一头牛可以换(3×6=18)只羊。
【详解】3×6=18(只)
所以,一头牛可以换18只羊。
【点睛】本题是一道简单的等量代换问题,考查了学生等量转换的能力。
10.48
【分析】通过观察图形可知,阴影部分的面积占大三角形面积的,把大三角形的面积看作单位“1”,根据已知一个数的几分之几是多少,求这个数,用除法解答。
【详解】21÷
=
=48(平方厘米)
【点睛】此题解答关键是求出阴影面积的面积占大三角形面积的几分之几,然后根据已知一个数的几分之几是多少,求这个数,用除法解答。
11. 555555555 72
【分析】根据积的变化规律:两数相乘,如果一个因数不变,另一个因数扩大或缩小几倍(0除外),积也会随之扩大或缩小相同的倍数,据此解答。
【详解】45÷9=5
所以,12345679×45=111111115×5=555555555;
888888888÷111111111=8
9×8=72
所以,12345679×72=888888888。
【点睛】本题考查了积的变化规律的运用。
12. 495 594 693 792 891
【分析】通过观察发现,两个因数中,第一个因数都是99,第二个因数依次多1,结果是9与第二个因数相乘中间是9即可。
【详解】因为:
99×1=99
99×2=198
99×3=297
99×4=396
所以:
99×5=495
99×6=594
99×7=693
99×8=792
99×9=891
【点睛】此题考查了学生观察能力,以及分析问题、总结规律的能力。
13.2
【分析】假设6支都是圆珠笔,则买6支圆珠笔需要42元,比实际情况少了10元,而每错看一支笔,会少算5元,可以先求出钢笔的数量,再计算圆珠笔的数量。
【详解】(52-6×7)÷(12-7)
=10÷5
=2(支)
所以钢笔买了2支。
【点睛】本题实质上考查的是鸡兔同笼问题,也可以假设买的都是钢笔,先求出圆珠笔的数量,再计算钢笔的数量。
14. 36 7n+1
【分析】观察可知,小棒数量=图形序号×7+1,据此分析。
【详解】5×7+1
=35+1
=36(根)
n×7+1=7n+1(根)
【点睛】数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
15. 5 14 62
【分析】观察可知,棋子数量=3n+2,据此列式计算。
【详解】3×1+2
=3+2
=5(个)
3×4+2
=12+2
=14(个)
3×20+2
=60+2
=62(个)
【点睛】数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
16.6n+2
【分析】第1个图形有8根火柴棒,第2个图形有14根火柴棒,第3个图形有20根火柴棒,观察不难发现:后一个图形比前一个图形多6根火柴棒,然后根据此规律写出第n个图形的火柴棒的根数即可。
【详解】据分析可知:第n个图形有(6n+2)根火柴棒。
【点睛】本题是对图形变化规律的考查,查出前三个图形的火柴棒的根数,并观察出后一个图形比前一个图形多6根火柴棒是解题的关键。
17.11
【分析】第一个图形周长是1+2=3(厘米),第二个图形的周长是:1+2×2=5(厘米),第三个图形的周长是:1+3×2=6(厘米),……,第n个图形的周长是:1+2n(厘米),据此解答即可。
【详解】第5个图形的周长是1+5×2=11厘米。
【点睛】本题考查数与形,解答本题的关键是找到规律。
18.4和2
【分析】根据题干,设香蕉每千克x元,则芒果每千克就是(x+2)元,根据等量关系:香蕉单价×数量+芒果单价×数量=总钱数26元,据此列出方程解决问题。
【详解】解:设香蕉每千克x元,则芒果每千克就是(x+2)元,
5×(x+2)+3x=26
5x+5×2+3x=26
8x+10=26
8x+10-10=26-10
8x=16
8x÷8=16÷8
x=2
2+2=4(元)
所以,每千克芒果和每千克香蕉分别是4和2元。
【点睛】此题属于两个未知数的问题,设一个未知数为x,另一个未知数用含有x的式子表示,再利用题干中的等量关系即可解答问题。
19.13+23+33+43+53+63=212
【分析】13+23=(1+2)2=32,13+23+33=(1+2+3)2=62,13+23+33+43=(1+2+3+4)2=102,所以13+23+33+43+53=(1+2+3+4+5)2=152,13+23+33+43+53+63=(1+2+3+4+5+6)2=212,即可解答。
【详解】由上面算式规律知:第5个等式是:13+23+33+43+53
=(1+2+3+4+5)2
=152;
第6个等式是:13+23+33+43+53+63
=(1+2+3+4+5+6)2
=212
13+23+33+43+53+63=212
【点评】本题考查学生分析数据,总结、归纳数据规律的能力,关键是找出规律,要求学生要有一定的解题技巧;根据题中所给的材料获取所需的信息和解题方法是需要掌握的基本技能。
20. 10 1+3n
【分析】可以想象原来就有1个菱形,再每增加3个菱形就增加1朵花型图案,所以摆3朵花型图案需要1+3×3=10(个)菱形,摆n个花型图案就需要(1+3n)个基本菱形。
【详解】据分析可知:摆3朵花型图案需要1+3×3=10(个)菱形,摆n个花型图案就需要(1+3n)个基本菱形。
【点睛】读懂题意,根据图形找出规律是解决此题的关键。
21.(1)48平方厘米;
(2)12.56平方厘米;
(3)36平方厘米
【分析】(1)通过平移可知,图中涂色部分的面积等于一个上底6厘米、下底10厘米,高6厘米的梯形的面积。
(2)通过平移可知,图中涂色部分的面积等于半径是4厘米的圆的面积;根据圆的面积公式:,先求出半径是4厘米的圆的面积,再除以4即可;
(3)通过平移可知,图中涂色部分的面积等于底12厘米、高12厘米的三角形面积的一半,根据“三角形面积=底×高÷2”,求出这个三角形的面积,再除以2即可。
【详解】(1)(6+10)×6÷2
=16×6÷2
=96÷2
=48(平方厘米)
(2)3.14×42÷4
=3.14×16÷4
=50.24÷4
=12.56(平方厘米)
(3)12×12÷2÷2
=144÷2÷2
=72÷2
=36(平方厘米)
22.288平方米
【分析】通过观察图形,我们可将中间的小路去除,将右侧图形向左侧平移,即可与左侧图形拼成一个新的长方形,新长方形的长减少1米,即可按照长方形面积=长×宽解答。
【详解】12×(25-1)
=12×24
=288(平方米)
答:种植花草的面积有288平方米。
【点睛】此题考查了学生解题的平移思想,根据平移即可将不规则图形变为规则图形,然后进行解答即可。
23.(1)5×=5-;作图见详解
(2)100×=100-
【分析】观察可知,第几个等式对应第一个乘数和第二个乘数的分子就是几,分母是分子+1;图形对应规律是第几个等式就将图形平均分成几份,分子是几涂几份。
【详解】(1)5×=5-;
(2)100×=100-
【点睛】在探索数与形结合的规律时,要考虑数的排列规律,通过数形结合、对应等方法来解决问题。
24.850个
【分析】根据已知条件,第一排有10个座位,后面每排都比前面一排多2个座位,则:第二排有:10+1×2=12(个);第三排有:10+2×2=14(个);第四排有:10+3×2=16(个)……第n排有:10+(n-1)×2;所以第25排有:10+(25-1)×2=58(个),据此求出第25排有多少个座位;
因为后面每一排的座位都比前一排多2个,所以座位排列为梯形,梯形的上底长为第一排座位数,下底长为最后一排座位数,高为排数;利用梯形面积公式“梯形面积=(上底+下底)×高÷2”解答。
【详解】10+(25-1)×2
=10+24×2
=10+48
=58(个)
(10+58)×25÷2
=68×25÷2
=1700÷2
=850(个)
答:解放路实验学校的报告厅一共有850个座位。
【点睛】灵活利用梯形的面积公式是解答题目的关键。
25.31场;63场
【分析】淘汰赛中,每一轮淘汰掉一半选手,直至产生最后的冠军;据此分别计算出每一轮比赛后剩下的人数,直到剩下1人时,就是冠军;再把每一轮剩下的人数相加求和,即可求出产生冠军共要比赛的场次。
【详解】(32÷2)+(32÷2÷2)+(32÷2÷2÷2)+(32÷2÷2÷2÷2)+(32÷2÷2÷2÷2÷2)
=16+(16÷2)+(16÷2÷2)+(16÷2÷2÷2)+(16÷2÷2÷2÷2)
=16+8+4+2+1
=31(场)
(64÷2)+(64÷2÷2)+(64÷2÷2÷2)+(64÷2÷2÷2÷2)+(64÷2÷2÷2÷2÷2)+(64÷2÷2÷2÷2÷2÷2)
=32+(32÷2)+(32÷2÷2)+(32÷2÷2÷2)+(32÷2÷2÷2÷2)+(32÷2÷2÷2÷2÷2)
=32+16+8+4+2+1
=63(场)
答:共要比赛31场。如果有64名选手参加比赛,产生冠军共要比赛63场。
【点睛】此题还可以这样解题:淘汰赛的比赛场次计算:有n个队参加,再淘汰掉(n-1)个队,共比赛(n-1)场。
26.3871平方米
【分析】观察图形可知,草坪的面积等于长(80-1)米、宽(50-1)米的长方形的面积,根据“长方形面积=长×宽”,即可解题。
【详解】(80-1)×(50-1)
=79×49
=3871(平方米)
答:草坪的面积是3871平方米。
【点睛】熟记长方形面积计算公式,是解答此题的关键。
27.15元;5元
【分析】根据“1支钢笔的价钱和3支圆珠笔的价钱一样多”,2支钢笔的价钱就等于6支圆珠笔的价钱,也就是60元钱相当于买了(2×3+6)支圆珠笔,用60元除以(2×3+6)支,求出圆珠笔的价格,再乘3,即可求出钢笔的价格。
【详解】将钢笔换成圆珠笔,可得:
60÷(2×3+6)
=60÷(6+6)
=60÷12
=5(元)
5×3=15(元)
答:每支钢笔每支是15元,圆珠笔每支是5元。
【点睛】解答此题时,也可以将圆珠笔换成钢笔,先计算出钢笔的价格,再计算出圆珠笔的价格。
28.(1)n(n+1);(2)①210;②7448。
【分析】(1)根据和等于加数的个数乘以首尾两个加数和的一半列式计算即可得解;
(2)①因为28=2×14,即n=14,根据S与n之间的关系:S=n(n+1),再把n=14代入计算即可;
②结合上述规律,只需加上2+4+…+102,按公式计算出结果再减去2+4+…+102即可。
【详解】(1)根据和等于加数的个数乘以首尾两个加数和的一半列式为:
S=2+4+6+…+2n
=(+1)×
=(n﹣1+1)(n+1)
=n(n+1);
(2)①因为28=2×14,即n=14,根据S与n之间的关系:S=n(n+1),
所以2+4+6+8+…+28
=14×(14+1)
=14×15
=210;
②104+106+108+…+200
=(2+4+6+…+198+200)﹣(2+4+6+…+102)
=100×101﹣51×52
=10100﹣2652
=7448。
【点睛】本题主要考查了规律型问题:数字的变化,解题时注意根据所给的具体式子观察结果和数据的个数之间的关系;认真观察、仔细思考,善用联想是解决这类问题的方法。
29.(1)8人;12人;(2n+4)人
(2)112
(3)100
【分析】(1)根据图示,发现这组图形的规律:1张桌子可坐人数:6人;2张桌子可坐人数:6+2=8(人);4张桌子可坐人数:6+2+2+2=12(人);…n张桌子可坐人数:6+2(n-1)=(2n+4)人。
(2)根据(1)的规律可知:5张桌子拼一块,可坐人数:2×5+4=14(人).40张桌子每5张拼一块,可坐人数:14×8=112(人)。
(3)由(1)知,每8张桌子拼一块,可坐人数:2×8+4=20(人),40张桌子每8张拼一块,可以拼成大桌子的个数:40÷8=5(张),可坐人数:20×5=100(人)。
据此解答.
【详解】(1)2张桌子可坐人数:6+2=8(人);4张桌子可坐人数:6+2+2+2=12(人);…n张桌子可坐人数:6+2(n-1)=(2n+4)人。
(2)5张桌子拼一块,可坐人数:2×5+4=14(人),40张桌子每5张拼一块,可坐人数:14×8=112(人)。
(3)每8张桌子拼一块,可坐人数:2×8+4=20(人),40张桌子每8张拼一块,可以拼成大桌子的个数:40÷8=5(张),可坐人数:20×5=100(人)。
【点睛】本题主要考查数与形结合的规律,关键根据所给图形发现这组图形的规律,并运用规律解决问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
苏教版小学数学
五年级下册第六单元质量调研卷
一、选择题(16分)
1.把一些鸡和兔放在同一只笼子里,从上面数有30个头,从下面数有64条腿。那么鸡比兔子多( )只。
A.15 B.20 C.26 D.28
2.根据规律算一算。
……
( )
A. B. C. D.
3.下图是由一个大正方形与一个小正方形拼成的,已知小正方形的边长为4cm,阴影部分的面积为28cm2。那么空白部分的面积为( )cm2。
A.20 B.24 C.28 D.32
4.观察下列式子:0.2=123÷999,0.3=237÷999,0.4=45÷999,那么,0.5等于( )。
A.0.45÷999 B.4.5÷999 C.45÷999 D.450÷999
5.把一根10米长的细绳分别围成以下三个图形,( )的面积最小。
A.长方形 B.正方形 C.圆 D.无法判断
6.根据37037×3=111111,37037×6=222222,37037×9=333333,那么37037×18=( )。
A.444444 B.555555 C.666666 D.999999
7.兴趣小组正在探索求下图组合图形的面积,其中( )的方法是错误的。
A.淘气:把图形分割成一个梯形和一个长方形,再求各部分面积的和
B.笑笑:把图形分割成一个三角形和一个梯形,再求各部分面积的和
C.奇思:把图形看成一个长方形,用其面积减去一个梯形的面积
D.妙想:把线绕图形围一周,再把这条线围成一个正方形,求正方形的面积
8.观察下面的算式:5×9=45
55×99=5445
555×999=554445
5555×9999=55544445
则5555555555×9999999999=( )。
A.5555555554444444445 B.5555555555444444444445
C.55555555544444444445
二、填空题(42分)
9.一头猪能换三只羊,一头牛能换六头猪,一头牛可以换_______只羊。
10.如图中阴影部分面积是21平方厘米,那么大三角形的面积是________平方厘米。
11.用计算器算得12345679×9=111111111请直接写出下面算式的得数:
12345679×45=_________;
12345679×________=888888888。
12.先找规律,再用规律填空。
99×1=99 99×2=198 99×3=297
99×4=396 99×5=( ) 99×6=( )
99×7=( ) 99×8=( ) 99×9=( )
13.钢笔每支12元,圆珠笔每支7元,共买6支,用了52元,钢笔买了( )支。
14.用小棒按照如下方式摆图形。摆第5个图形需要________根小棒,摆第n个图形需要________根小棒。
15.按如图所示用棋子摆成反写“T”字,第1个反写“T”字需要________个棋子,第4个反写“T”字需要________个棋子;按这样的规律摆下去,第20个反写“T”字需要________个棋子。
16.为庆祝六一儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛。如图所示:
按照上面的规律,摆n个“金鱼”需用火柴棒的根数为________。
17.如下图,如果一个小三角形的边长为1厘米,那么第5个图形的周长是( )厘米。
18.张老师买了5千克芒果和3千克香蕉用去了26元。每千克芒果比每千克香蕉贵2元,每千克芒果和每千克香蕉分别是_______元。
19.已知下列等式:13=12,13+23=32,13+23+33=62,13+23+33+43=102……由此规律知,第6个等式是________。
20.下列漂亮的花型图案是由基本的菱形摆成的。
如果我们要摆三朵花型图案,需要________个基本菱形,如果摆n个又需要________个基本菱形。
三、图形计算(12分)
21.求下面各图形涂色部分的面积。
(1)(2) (3)
四、解答题(30分)
22.两幢教学楼之间有一个长方形空地,中间是一条宽1米的鹅卵石小路,其余部分都种植了花草。种植花草的面积有多大?
23.观察下面的等式和相应的图形(每一个正方形的边长均为1),探究其中的规律:
①1×=1-←→
②2×=2-←→
③3×=3-←→
④4×=4-←→
(1)写出第5个等式,并在下面给出的5个正方形上画出与之对应的图形。
________←→
(2)猜想并写出与第100个图形相对应的等式。
24.解放路实验学校报告厅共有25排座位。其中第一排有10个座位,第二排有12个座位,后面每一排的座位都比前一排多2个。解放路实验学校的报告厅一共有多少个座位?
25.“海象杯”少儿围棋赛共有32名选手参加,比赛采用单场淘汰制,要决出冠军,共要比赛多少场?如果有64名选手参加比赛,产生冠军共要比赛多少场?
26.一块长80米、宽50米的长方形绿化带,中间有两条宽1米的小路,其余地方为草坪。草坪的面积是多少平方米?
27.王老师买了2支钢笔和6支圆珠笔,共付60元,已知1支钢笔的价钱和3支圆珠笔的价钱一样多,每支钢笔和每支圆珠笔各多少元?
28.从2开始,连续的偶数相加,它们和的情况如下:
2=1×2
2+4=6=2×3
2+4+6=12=3×4
2+4+6+8=20=4×5
2+4+6+8+10=30=5×6
……
(1)根据表中的规律猜想,用n的式子表示s的公式为S=2+4+6+8+…+2n=_____。
(2)根据上题的规律计算①2+4+6+8+…+28
②104+106+108+…+200
29.
(1)2张桌子拼在一起可坐多少人?4张桌子呢?n张桌子呢?(n为非0自然数)
(2)一家餐厅有40张这样的长方形桌子,按照上图方式每5张拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐________人。
(3)在(2)题中,若改成每8张桌子拼成1张大桌子,则共可坐________人。
参考答案:
1.C
【分析】从题中可知鸡兔共有30只,假设30只都是兔子,则会有腿4×30=120(条)比实际多出了120-64=56(条),一只兔子比一只鸡多两条腿,则鸡的只数就是:56÷(4-2)=28(只),兔子只数是30-28=2(只),从而也可求出鸡比兔子多的只数。
【详解】假设30只动物都是兔子,则鸡的只数:
(4×30-64)÷(4-2)
=56÷2=28(只)
30-28=2(只)
28-2=26(只)
答:鸡比兔子多26只。
故答案为:C。
【点睛】解这类题的关键是用假设法进行分析,进而得出结论,也可以用方程进行解答。
2.D
【解析】从所给算式可以看出:算式等号左边都是连续的偶数,右边的结果为:偶数的个数×(个数+1),即n×(n+1),据此解答。
【详解】由分析可得,10×(10+1)=10×11;
故答案为:D
【点睛】观察特例特点,找出规律,根据规律进行解答。
3.B
【分析】阴影部分是由一个三角形和小正方形组成的。正方形的面积=边长×边长,据此可以求出小正方形的面积。用阴影部分的面积减去小正方形的面积即是三角形的面积,三角形的高是4厘米,根据三角形的面积=底×高÷2,可以求出三角形的底,即是大正方形的边长。求出大正方形的面积,再减去三角形的面积就是空白部分的面积。
【详解】28-4×4=12(平方厘米)
12×2÷4=6(厘米)
6×6-12=24(平方厘米)
故答案为:B
【点睛】用阴影部分的面积减去小正方形的面积求出三角形的面积,继而求出三角形的底是解题的关键。
4.D
【分析】观察已知三个算式,当除数是999时,将被除数小数点向左移动3位,然后在十分位和千分位的数字上加上循环符号,就是算式的商,据此反推。
【详解】观察已知三个算式,当除数是999时,将被除数小数点向左移动3位,然后在十分位和千分位的数字上加上循环符号,就是算式的商,
所以,已知商为0.5,将循环符号去掉,然后小数点向右移动三位就是被除数,即450,得到算式:0.5=450÷999
故选:D。
【点睛】本题主要考查了“式”的规律,发现已知算式商和被除数之间的关系,是本题解题的关键。
5.A
【分析】已知三个图形的周长,可以根据圆的周长公式可得r=C÷π÷2,再根据圆的面积公式S=πr2,求出圆的面积;根据正方形的周长公式可得a=C÷4,求出正方形的边长,再根据正方形的面积=a2,求出正方形的面积;周长一定,也就是长方形长与宽的和一定,当长与宽越接近时面积越大,当长与宽相等时面积最大,此时是正方形,也就是正方形的面积大于长方形的面,再比较求出圆的面积和正方形的面积即可得出结论。
【详解】(1)圆的半径:10÷3.14÷2≈1.6(米);
则圆的面积为:3.14×1.62=8.0384(平方米)
(2)正方形的面积:正方形的边长为10÷4=2.5(米)
正方形面积为:2.5×2.5=6.25(平方米)
(3)而周长一定时正方形的面积比长方形的面积大
8.0384>6.25,
由以上计算可以得出,当周长一定时,圆的面积最大,长方形的面积最小。
故答案选:A
【点睛】解决本题要明确:周长相等的平面图形中,圆的面积最大;以及两个数的和一定,这两个数越接近时乘积越大。
6.C
【分析】根据积的变化规律:一个因数不变,另一个因数扩大到原来的多少倍(0除外),积也扩大到原来的多少倍,据此解答即可。
【详解】37037×3=111111
37037×6=222222
37037×9=333333
那么37037×18=666666
故本题答案为:C。
【点评】通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力。
7.D
【分析】根据组合图形面积的意义逐项分析。
【详解】A.如图所示:,把图形分割成一个梯形和一个长方形,再求各部分面积的和即是组合图形的面积,此方法正确;
B.如图所示:,把图形分割成一个三角形和一个梯形,再求各部分面积的和即是组合图形的面积,此方法正确;
C.如图所示:,把图形看成一个长方形,用其面积减去一个梯形的面积即是组合图形的面积,此方法正确;
D.把线绕图形围一周,再把这条线围成一个正方形,这个正方形和这个组合图形的周长相等,但面积不一定相等,此方法错误。
故答案为:D
【点睛】本题考查组合图形的面积,一般用“分割法”或“添补法”解答。
8.C
【分析】通过观察,55×99=5445,555×999=554445,5555×9999=55544445,得出规律:各位数字都是5和各位数字都是9的n位数相乘,结果中前n﹣1位数字是5,接着n位数字是4,个位数字是5;当n=10时,代入,即可得解。
【详解】55×99=5445
555×999=554445
5555×9999=55544445;
555555555×999999999=55555555544444444445;
故答案为:C。
【点睛】认真分析,找出算式中的规律,是解决此题的关键。
9.18
【分析】一头牛能换六头猪,一头猪能换三只羊,根据乘法的意义可知一头牛可以换(3×6=18)只羊。
【详解】3×6=18(只)
所以,一头牛可以换18只羊。
【点睛】本题是一道简单的等量代换问题,考查了学生等量转换的能力。
10.48
【分析】通过观察图形可知,阴影部分的面积占大三角形面积的,把大三角形的面积看作单位“1”,根据已知一个数的几分之几是多少,求这个数,用除法解答。
【详解】21÷
=
=48(平方厘米)
【点睛】此题解答关键是求出阴影面积的面积占大三角形面积的几分之几,然后根据已知一个数的几分之几是多少,求这个数,用除法解答。
11. 555555555 72
【分析】根据积的变化规律:两数相乘,如果一个因数不变,另一个因数扩大或缩小几倍(0除外),积也会随之扩大或缩小相同的倍数,据此解答。
【详解】45÷9=5
所以,12345679×45=111111115×5=555555555;
888888888÷111111111=8
9×8=72
所以,12345679×72=888888888。
【点睛】本题考查了积的变化规律的运用。
12. 495 594 693 792 891
【分析】通过观察发现,两个因数中,第一个因数都是99,第二个因数依次多1,结果是9与第二个因数相乘中间是9即可。
【详解】因为:
99×1=99
99×2=198
99×3=297
99×4=396
所以:
99×5=495
99×6=594
99×7=693
99×8=792
99×9=891
【点睛】此题考查了学生观察能力,以及分析问题、总结规律的能力。
13.2
【分析】假设6支都是圆珠笔,则买6支圆珠笔需要42元,比实际情况少了10元,而每错看一支笔,会少算5元,可以先求出钢笔的数量,再计算圆珠笔的数量。
【详解】(52-6×7)÷(12-7)
=10÷5
=2(支)
所以钢笔买了2支。
【点睛】本题实质上考查的是鸡兔同笼问题,也可以假设买的都是钢笔,先求出圆珠笔的数量,再计算钢笔的数量。
14. 36 7n+1
【分析】观察可知,小棒数量=图形序号×7+1,据此分析。
【详解】5×7+1
=35+1
=36(根)
n×7+1=7n+1(根)
【点睛】数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
15. 5 14 62
【分析】观察可知,棋子数量=3n+2,据此列式计算。
【详解】3×1+2
=3+2
=5(个)
3×4+2
=12+2
=14(个)
3×20+2
=60+2
=62(个)
【点睛】数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
16.6n+2
【分析】第1个图形有8根火柴棒,第2个图形有14根火柴棒,第3个图形有20根火柴棒,观察不难发现:后一个图形比前一个图形多6根火柴棒,然后根据此规律写出第n个图形的火柴棒的根数即可。
【详解】据分析可知:第n个图形有(6n+2)根火柴棒。
【点睛】本题是对图形变化规律的考查,查出前三个图形的火柴棒的根数,并观察出后一个图形比前一个图形多6根火柴棒是解题的关键。
17.11
【分析】第一个图形周长是1+2=3(厘米),第二个图形的周长是:1+2×2=5(厘米),第三个图形的周长是:1+3×2=6(厘米),……,第n个图形的周长是:1+2n(厘米),据此解答即可。
【详解】第5个图形的周长是1+5×2=11厘米。
【点睛】本题考查数与形,解答本题的关键是找到规律。
18.4和2
【分析】根据题干,设香蕉每千克x元,则芒果每千克就是(x+2)元,根据等量关系:香蕉单价×数量+芒果单价×数量=总钱数26元,据此列出方程解决问题。
【详解】解:设香蕉每千克x元,则芒果每千克就是(x+2)元,
5×(x+2)+3x=26
5x+5×2+3x=26
8x+10=26
8x+10-10=26-10
8x=16
8x÷8=16÷8
x=2
2+2=4(元)
所以,每千克芒果和每千克香蕉分别是4和2元。
【点睛】此题属于两个未知数的问题,设一个未知数为x,另一个未知数用含有x的式子表示,再利用题干中的等量关系即可解答问题。
19.13+23+33+43+53+63=212
【分析】13+23=(1+2)2=32,13+23+33=(1+2+3)2=62,13+23+33+43=(1+2+3+4)2=102,所以13+23+33+43+53=(1+2+3+4+5)2=152,13+23+33+43+53+63=(1+2+3+4+5+6)2=212,即可解答。
【详解】由上面算式规律知:第5个等式是:13+23+33+43+53
=(1+2+3+4+5)2
=152;
第6个等式是:13+23+33+43+53+63
=(1+2+3+4+5+6)2
=212
13+23+33+43+53+63=212
【点评】本题考查学生分析数据,总结、归纳数据规律的能力,关键是找出规律,要求学生要有一定的解题技巧;根据题中所给的材料获取所需的信息和解题方法是需要掌握的基本技能。
20. 10 1+3n
【分析】可以想象原来就有1个菱形,再每增加3个菱形就增加1朵花型图案,所以摆3朵花型图案需要1+3×3=10(个)菱形,摆n个花型图案就需要(1+3n)个基本菱形。
【详解】据分析可知:摆3朵花型图案需要1+3×3=10(个)菱形,摆n个花型图案就需要(1+3n)个基本菱形。
【点睛】读懂题意,根据图形找出规律是解决此题的关键。
21.(1)48平方厘米;
(2)12.56平方厘米;
(3)36平方厘米
【分析】(1)通过平移可知,图中涂色部分的面积等于一个上底6厘米、下底10厘米,高6厘米的梯形的面积。
(2)通过平移可知,图中涂色部分的面积等于半径是4厘米的圆的面积;根据圆的面积公式:,先求出半径是4厘米的圆的面积,再除以4即可;
(3)通过平移可知,图中涂色部分的面积等于底12厘米、高12厘米的三角形面积的一半,根据“三角形面积=底×高÷2”,求出这个三角形的面积,再除以2即可。
【详解】(1)(6+10)×6÷2
=16×6÷2
=96÷2
=48(平方厘米)
(2)3.14×42÷4
=3.14×16÷4
=50.24÷4
=12.56(平方厘米)
(3)12×12÷2÷2
=144÷2÷2
=72÷2
=36(平方厘米)
22.288平方米
【分析】通过观察图形,我们可将中间的小路去除,将右侧图形向左侧平移,即可与左侧图形拼成一个新的长方形,新长方形的长减少1米,即可按照长方形面积=长×宽解答。
【详解】12×(25-1)
=12×24
=288(平方米)
答:种植花草的面积有288平方米。
【点睛】此题考查了学生解题的平移思想,根据平移即可将不规则图形变为规则图形,然后进行解答即可。
23.(1)5×=5-;作图见详解
(2)100×=100-
【分析】观察可知,第几个等式对应第一个乘数和第二个乘数的分子就是几,分母是分子+1;图形对应规律是第几个等式就将图形平均分成几份,分子是几涂几份。
【详解】(1)5×=5-;
(2)100×=100-
【点睛】在探索数与形结合的规律时,要考虑数的排列规律,通过数形结合、对应等方法来解决问题。
24.850个
【分析】根据已知条件,第一排有10个座位,后面每排都比前面一排多2个座位,则:第二排有:10+1×2=12(个);第三排有:10+2×2=14(个);第四排有:10+3×2=16(个)……第n排有:10+(n-1)×2;所以第25排有:10+(25-1)×2=58(个),据此求出第25排有多少个座位;
因为后面每一排的座位都比前一排多2个,所以座位排列为梯形,梯形的上底长为第一排座位数,下底长为最后一排座位数,高为排数;利用梯形面积公式“梯形面积=(上底+下底)×高÷2”解答。
【详解】10+(25-1)×2
=10+24×2
=10+48
=58(个)
(10+58)×25÷2
=68×25÷2
=1700÷2
=850(个)
答:解放路实验学校的报告厅一共有850个座位。
【点睛】灵活利用梯形的面积公式是解答题目的关键。
25.31场;63场
【分析】淘汰赛中,每一轮淘汰掉一半选手,直至产生最后的冠军;据此分别计算出每一轮比赛后剩下的人数,直到剩下1人时,就是冠军;再把每一轮剩下的人数相加求和,即可求出产生冠军共要比赛的场次。
【详解】(32÷2)+(32÷2÷2)+(32÷2÷2÷2)+(32÷2÷2÷2÷2)+(32÷2÷2÷2÷2÷2)
=16+(16÷2)+(16÷2÷2)+(16÷2÷2÷2)+(16÷2÷2÷2÷2)
=16+8+4+2+1
=31(场)
(64÷2)+(64÷2÷2)+(64÷2÷2÷2)+(64÷2÷2÷2÷2)+(64÷2÷2÷2÷2÷2)+(64÷2÷2÷2÷2÷2÷2)
=32+(32÷2)+(32÷2÷2)+(32÷2÷2÷2)+(32÷2÷2÷2÷2)+(32÷2÷2÷2÷2÷2)
=32+16+8+4+2+1
=63(场)
答:共要比赛31场。如果有64名选手参加比赛,产生冠军共要比赛63场。
【点睛】此题还可以这样解题:淘汰赛的比赛场次计算:有n个队参加,再淘汰掉(n-1)个队,共比赛(n-1)场。
26.3871平方米
【分析】观察图形可知,草坪的面积等于长(80-1)米、宽(50-1)米的长方形的面积,根据“长方形面积=长×宽”,即可解题。
【详解】(80-1)×(50-1)
=79×49
=3871(平方米)
答:草坪的面积是3871平方米。
【点睛】熟记长方形面积计算公式,是解答此题的关键。
27.15元;5元
【分析】根据“1支钢笔的价钱和3支圆珠笔的价钱一样多”,2支钢笔的价钱就等于6支圆珠笔的价钱,也就是60元钱相当于买了(2×3+6)支圆珠笔,用60元除以(2×3+6)支,求出圆珠笔的价格,再乘3,即可求出钢笔的价格。
【详解】将钢笔换成圆珠笔,可得:
60÷(2×3+6)
=60÷(6+6)
=60÷12
=5(元)
5×3=15(元)
答:每支钢笔每支是15元,圆珠笔每支是5元。
【点睛】解答此题时,也可以将圆珠笔换成钢笔,先计算出钢笔的价格,再计算出圆珠笔的价格。
28.(1)n(n+1);(2)①210;②7448。
【分析】(1)根据和等于加数的个数乘以首尾两个加数和的一半列式计算即可得解;
(2)①因为28=2×14,即n=14,根据S与n之间的关系:S=n(n+1),再把n=14代入计算即可;
②结合上述规律,只需加上2+4+…+102,按公式计算出结果再减去2+4+…+102即可。
【详解】(1)根据和等于加数的个数乘以首尾两个加数和的一半列式为:
S=2+4+6+…+2n
=(+1)×
=(n﹣1+1)(n+1)
=n(n+1);
(2)①因为28=2×14,即n=14,根据S与n之间的关系:S=n(n+1),
所以2+4+6+8+…+28
=14×(14+1)
=14×15
=210;
②104+106+108+…+200
=(2+4+6+…+198+200)﹣(2+4+6+…+102)
=100×101﹣51×52
=10100﹣2652
=7448。
【点睛】本题主要考查了规律型问题:数字的变化,解题时注意根据所给的具体式子观察结果和数据的个数之间的关系;认真观察、仔细思考,善用联想是解决这类问题的方法。
29.(1)8人;12人;(2n+4)人
(2)112
(3)100
【分析】(1)根据图示,发现这组图形的规律:1张桌子可坐人数:6人;2张桌子可坐人数:6+2=8(人);4张桌子可坐人数:6+2+2+2=12(人);…n张桌子可坐人数:6+2(n-1)=(2n+4)人。
(2)根据(1)的规律可知:5张桌子拼一块,可坐人数:2×5+4=14(人).40张桌子每5张拼一块,可坐人数:14×8=112(人)。
(3)由(1)知,每8张桌子拼一块,可坐人数:2×8+4=20(人),40张桌子每8张拼一块,可以拼成大桌子的个数:40÷8=5(张),可坐人数:20×5=100(人)。
据此解答.
【详解】(1)2张桌子可坐人数:6+2=8(人);4张桌子可坐人数:6+2+2+2=12(人);…n张桌子可坐人数:6+2(n-1)=(2n+4)人。
(2)5张桌子拼一块,可坐人数:2×5+4=14(人),40张桌子每5张拼一块,可坐人数:14×8=112(人)。
(3)每8张桌子拼一块,可坐人数:2×8+4=20(人),40张桌子每8张拼一块,可以拼成大桌子的个数:40÷8=5(张),可坐人数:20×5=100(人)。
【点睛】本题主要考查数与形结合的规律,关键根据所给图形发现这组图形的规律,并运用规律解决问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
