方程的简单变形[下学期]

课件14张PPT。 1.方程的简单变形第六章 解一元一次方程《数学》(华师大.七年级 下册) 什么叫代数式、什么叫等式？代 数 式 与 等 式答：用运算符号连接数字与字母的式子叫代数式；含有等号的式子叫等式； 你能区分代数式与等式吗？下列式中哪些是代数式？
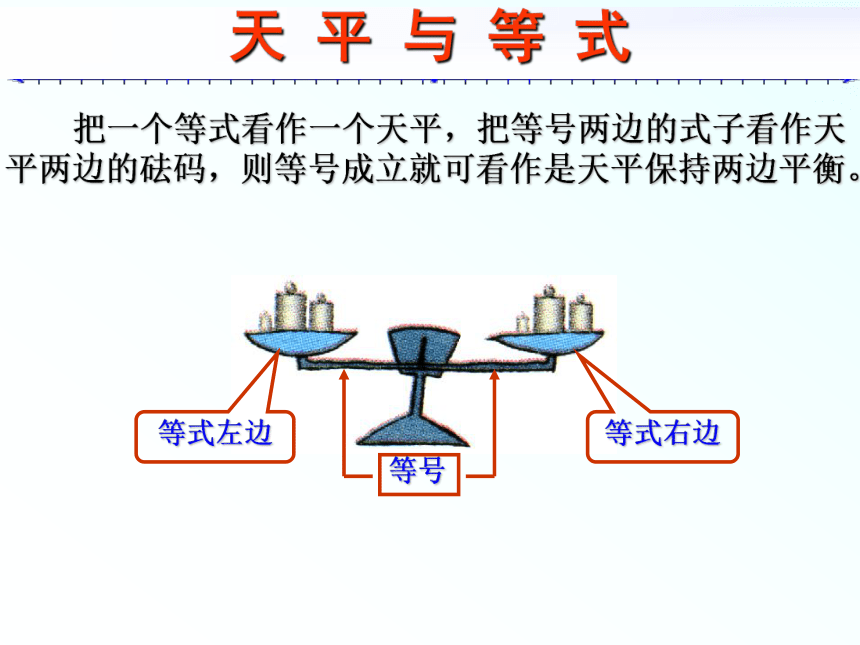
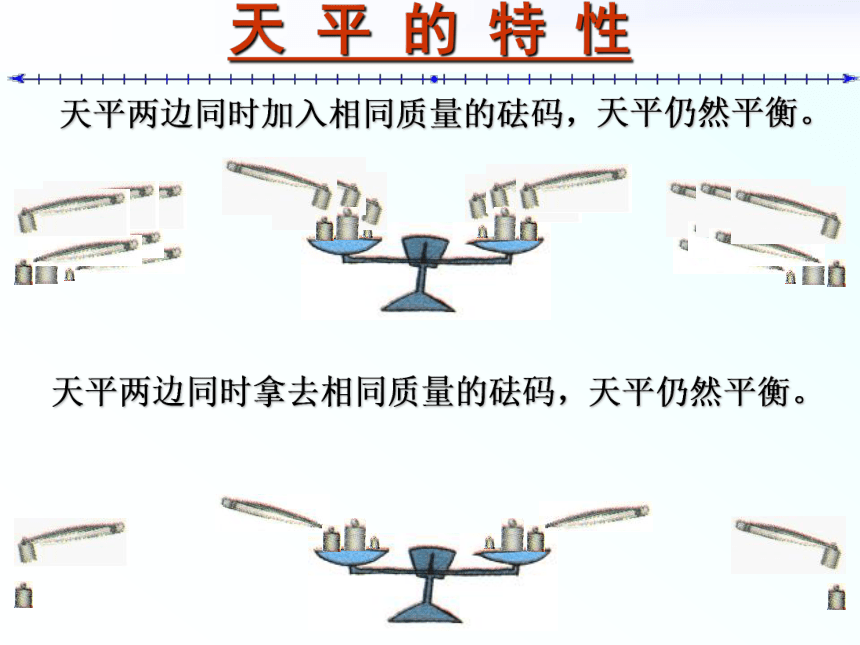
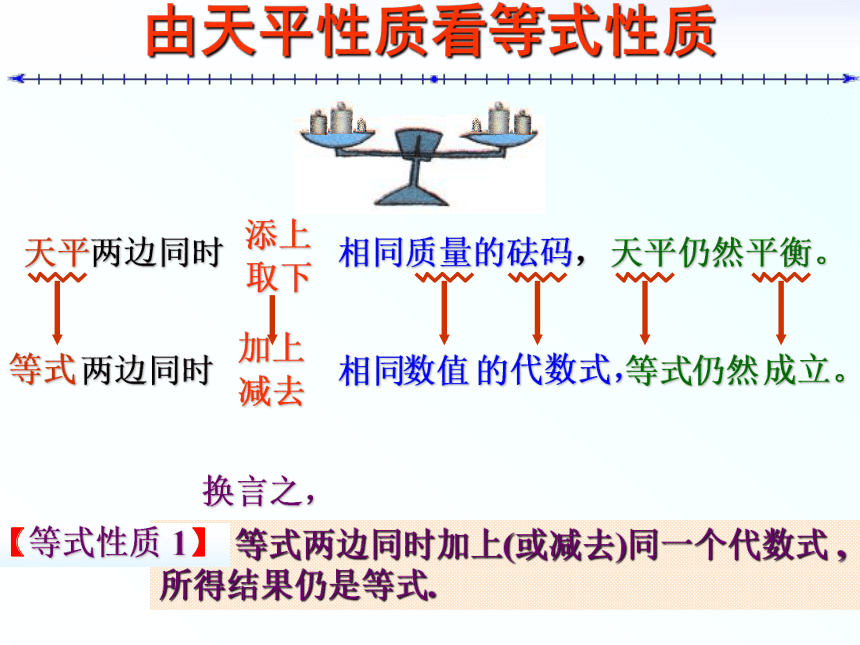
哪些是等式？?～?是代数式；?～?是等式。等号是大小关系符号中的一种。天 平 与 等 式 把一个等式看作一个天平，把等号两边的式子看作天平两边的砝码，则等号成立就可看作是天平保持两边平衡。天 平 的 特 性天平两边同时加入相同质量的砝码，天平仍然平衡。天平两边同时拿去相同质量的砝码，天平仍然平衡。由天平性质看等式性质天平两边同时天平仍然平衡。添上取下相同质量的砝码，等式加上减去数值代数式，等式成立。换言之， 等式两边同时加上(或减去)同一个代数式 ,
所得结果仍是等式.【等式性质 1】等 式 的 性 质 如果天平两边砝码的质量同时扩大相同的倍数(或同时缩小为原来的几分之一)，那么天平还保持两边平衡吗? 于是 , 你又能得出等式的什么性质?
试用准确、简明的语言叙述之. 等式两边同时乘同一个数 (或除以同一个非零的数) , 【等式性质 2】所得结果仍是等式.代数式数代数式包括了数，且可能含有字母。用等式的性质解方程 例1 解下列方程：
(1) x －5 = 7 ; (2) x ＋ 6 =2 ；
(3) 4x = 3x－4; (4) 3 y－1= 2y－5 .归 纳 像这样，将方程两边都加上(或减去)
同一个数或同一个整式，就相当于把方程中的某些项改变符号后，从方程的一边移到另一边，这样的变形叫做移项。
　注意：“移项”是指将方程的某些项从
等号的左边移到右边或从右边移到左边，
移项时要变号。用等式的性质解方程 例2 解下列方程：

(1) -5x = 2 ; (2) 例3 小明编了这样一道题：我是4月
出生的，我的年龄的2倍加上8，正好是
我出生那一月的总天数。你猜我有几岁？解 题 后 的 反 思(1) 怎样才叫做“方程解完了”;
(2) 使用等式的两个性质
对方程两边进行“同加减” 、 “同乘除”的目的是什么?(3) 对方程两边进行 “同加减” 、 “同乘除”,
可看作是对方程的两种变形 ,你能另一个角度来理解它们吗? x + b = c ? x = c－b已知和与一加数，求另一加数；已知积与一因数，求另一因数；本节课你的收获是什么？
　　这节课我们利用天平原理得出了等式的两个性质，并初步学习了用等式的两个性质解简单方程。 所谓“方程解完了”，意味着经过对原方程的一系列变形(两边同加减、乘除)，最终把方程化为最简的形式：
x = c
即方程左边只一个未知数项、右边只一个常数项，且未知数项的系数是 1.用等式的性质解方程 例4 解下列方程：

(1) 8x = 2x－7 ; (2) 6 = 8＋2x；
(3) 2y－ = y－3 ;
(4) 10m+5= 17m－5－2m.
方程知识的应用 例5 方程 2x＋1＝3和方程2x－a＝0
的解相同，求a的值.
变式：关于x的方程 2x－k＋5＝0的根

为－1，求代数式k2－3k－4的值.
P7 习 题 6.2.1的第1~3题.
作业