华师大七年级下多边形的内角和[下学期]
文档属性
| 名称 | 华师大七年级下多边形的内角和[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 190.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-04-04 00:00:00 | ||
图片预览


文档简介
课件10张PPT。多边形的内角和
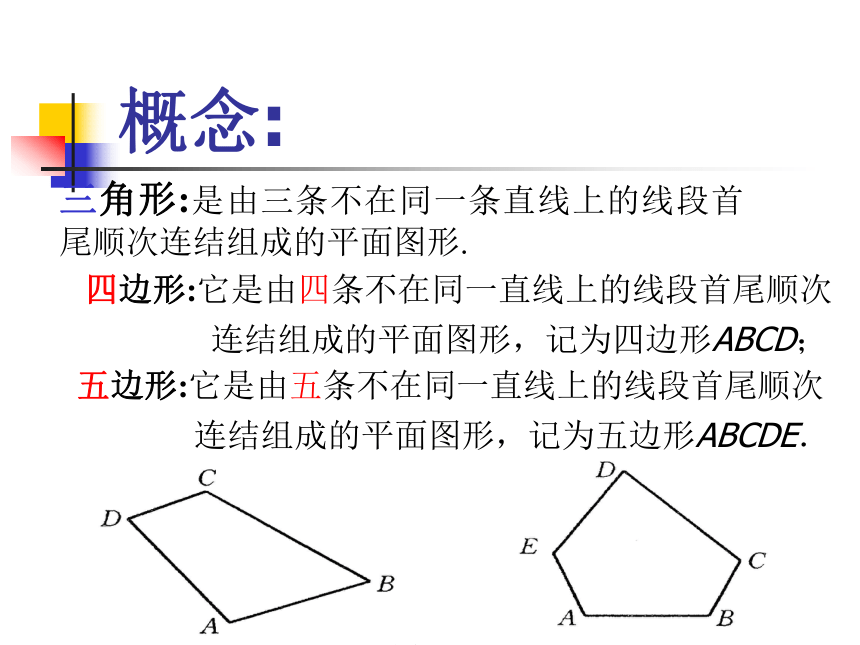
概念: 四边形:它是由四条不在同一直线上的线段首尾顺次
连结组成的平面图形,记为四边形ABCD;
五边形:它是由五条不在同一直线上的线段首尾顺次
连结组成的平面图形,记为五边形ABCDE.
三角形:是由三条不在同一条直线上的线段首尾顺次连结组成的平面图形.
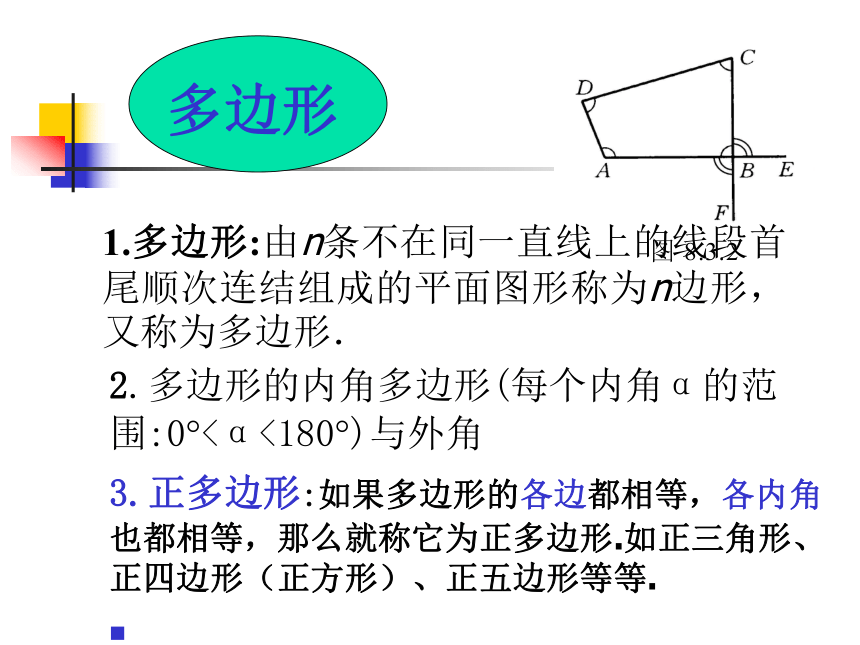
1.多边形:由n条不在同一直线上的线段首尾顺次连结组成的平面图形称为n边形,又称为多边形.
多边形 2.多边形的内角多边形(每个内角α的范围:0?<α<180?)与外角 3.正多边形:如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形.如正三角形、正四边形(正方形)、正五边形等等.
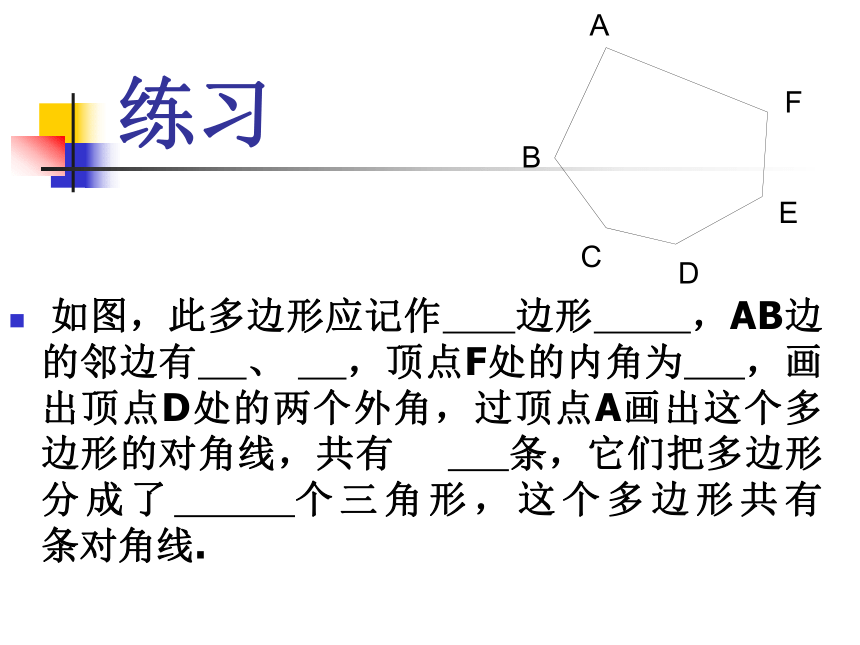
练习 如图,此多边形应记作 边形 ,AB边的邻边有 、 ,顶点F处的内角为 ,画出顶点D处的两个外角,过顶点A画出这个多边形的对角线,共有 条,它们把多边形分成了 个三角形,这个多边形共有 条对角线.
对角线 : 2.凸多边形对角线的条数
能否说明理由?
1. 对角线:连结多边形不相邻的两个顶点的线段叫做多边形的对角线. 试一试 1.一个三角形的内角和等于180°,
2.那么四边形的内角和等于多少呢?
3.五边形、六边形呢?
4.由此,n边形的内角和等于多少呢?
探 索 为了求得n边形的内角和,请根据图8.3.4所示,完成表8.3.1.
得到定理:n边形的内角和等于(n-2)·180?.
说明:
(1)多边形的内角和仅与边数有关,与多边形的大小、形状
无关;
(2)强调凸多边形的内角?的范围:0?结论:例题精选 例1
(1)22边形的内角和是多少度?若它的每一个
内角都相等,那么它的每个外角度数是多少?
(2)几边形的内角和是八边形内角和的2倍?
(3)几边形的内角和是2160??是否存在一个多边
形的内角和为1000??
例2 已知多边形的每个内角都是135?,求这个多边形的边数;
*例3?某多边形除一个角α外,其余内角的和是2750?.求这个多边形的边数.
(2)已知n边形恰有四个内角是钝角.这种多边形共有多少个?其中边数最少的是几边形?边数最多的是几边形?
连结组成的平面图形,记为四边形ABCD;
五边形:它是由五条不在同一直线上的线段首尾顺次
连结组成的平面图形,记为五边形ABCDE.
三角形:是由三条不在同一条直线上的线段首尾顺次连结组成的平面图形.
1.多边形:由n条不在同一直线上的线段首尾顺次连结组成的平面图形称为n边形,又称为多边形.
多边形 2.多边形的内角多边形(每个内角α的范围:0?<α<180?)与外角 3.正多边形:如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形.如正三角形、正四边形(正方形)、正五边形等等.
练习 如图,此多边形应记作 边形 ,AB边的邻边有 、 ,顶点F处的内角为 ,画出顶点D处的两个外角,过顶点A画出这个多边形的对角线,共有 条,它们把多边形分成了 个三角形,这个多边形共有 条对角线.
对角线 : 2.凸多边形对角线的条数
能否说明理由?
1. 对角线:连结多边形不相邻的两个顶点的线段叫做多边形的对角线. 试一试 1.一个三角形的内角和等于180°,
2.那么四边形的内角和等于多少呢?
3.五边形、六边形呢?
4.由此,n边形的内角和等于多少呢?
探 索 为了求得n边形的内角和,请根据图8.3.4所示,完成表8.3.1.
得到定理:n边形的内角和等于(n-2)·180?.
说明:
(1)多边形的内角和仅与边数有关,与多边形的大小、形状
无关;
(2)强调凸多边形的内角?的范围:0?结论:例题精选 例1
(1)22边形的内角和是多少度?若它的每一个
内角都相等,那么它的每个外角度数是多少?
(2)几边形的内角和是八边形内角和的2倍?
(3)几边形的内角和是2160??是否存在一个多边
形的内角和为1000??
例2 已知多边形的每个内角都是135?,求这个多边形的边数;
*例3?某多边形除一个角α外,其余内角的和是2750?.求这个多边形的边数.
(2)已知n边形恰有四个内角是钝角.这种多边形共有多少个?其中边数最少的是几边形?边数最多的是几边形?
