8.4 向量的应用(第2课时)教学课件(共16张PPT)
文档属性
| 名称 | 8.4 向量的应用(第2课时)教学课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 783.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 上教版(2020) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-04 09:43:17 | ||
图片预览






文档简介
(共16张PPT)
2022-2023学年高一数学同步精品课堂(沪教版2020必修第二册)
第 8 章 平面向量
8.4 向量的应用 (第2课时)
8.4 向量的应用
例5 如图8-4-4,平面上A、B、C三点的坐标分别是
(2,3)、(2,0)、(1,1).已知小明在点B 处休憩,有只小狗沿着
AC所在直线来回跑动.问:其在什么位置时,离小明最近?
记 则
设D 是直线AC上随着小狗跑动而动态变化的点,则 可
写成 的形式,λ是实数.问题转化为:确定λ的值,使向量
的模| |取到最小值,此时向量
??
的终点D 即为小狗离小明最近的位置
如果D 为D0使得, , 即 ,那么向量
的模取到最小值.于是,λ要满足 ,即
= 故
从而 最终推出
D0的坐标是
因此,当其在点 时,离小明最近.
例6 用向量方法证明:
证明 如图8-4-5,建立平面直角坐标系,并设A、B是单
位圆上的任意两点,而角α与β都是顶点在原点O、始边为 x 轴
正半轴的角,其终边分别落在AB与OB上.考虑向量
我们要求出 (的余弦).注意到交换α与β不影响要
证明的公式,可以假设从 旋转到 的最小正角就是 .这
个角与角α-β有相同的始边与终边,于是
又由于| =| |=1,我们得到
另一方面,用向量的坐标表示来计算数量积,我们有
综上所述,
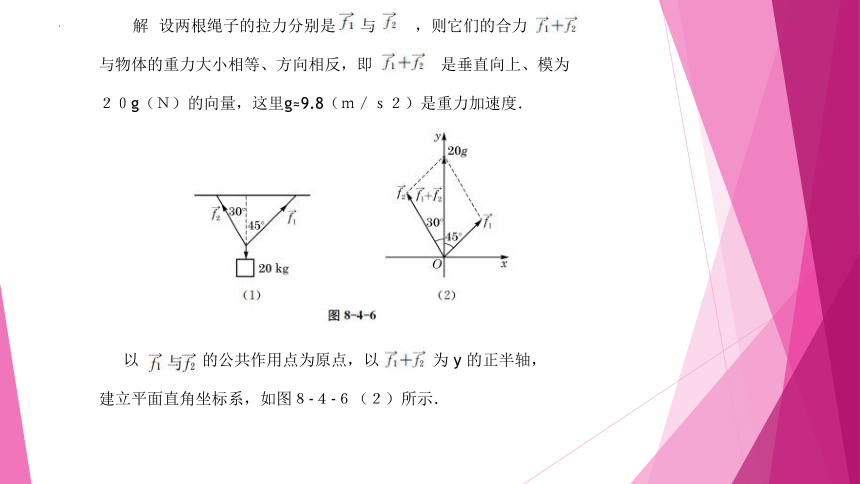
例7 将质量为20kg的物体用两根绳子悬挂起来,如图
8-4-6(1),两根绳子与铅垂线的夹角分别为45°与30°.求
它们分别提供的拉力的大小.(结果精确到0.1N)
解 设两根绳子的拉力分别是 与 ,则它们的合力
与物体的重力大小相等、方向相反,即 是垂直向上、模为
20g(N)的向量,这里g≈9.8(m/s2)是重力加速度.
以 的公共作用点为原点,以 为 y 的正半轴,
建立平面直角坐标系,如图8-4-6(2)所示.
令 则
因为 所以
解得
综上所述,这两根绳子所提供的拉力分别约为101.5N和
143.5N.
1. 问题转化,即把物理问题转化为数学问题;
用向量方法解决物理学中的相关问题的步骤:
2. 建立模型,即建立以向量为载体的数学模型;
3. 求解参数,即求向量的模、夹角、数量积等;
4. 回答问题,即把所得的数学结论回归到物理问题中.
课本练习
练习8.4(2)
1.已知两个力(单位:: 的夹角为60°,其中 (2.0).
某质点在这两个力的共同作用下,由点A(1,1)移动至点b(6,6)(单位:m).
(1)求 ;
(2)求 与 的合力对质点所做的功.
2.已知平面上三点A、B、C的坐标分别是(1,7)、(2,2)、(0,1),P为直
线AC上的一动点.问:P在什么位置时, 取到最小值?
随堂检测
1. 一物体在力F的作用下,由点A(20, 15)移动到点B(7, 0). 已知F=(4, -5),求F对该物体所做的功.
2. 如图,一滑轮组中有两个定滑轮A,B,在从连接点O出发的三根绳的端点处,挂着3个重物,它们所受的重力分别为4 N,4 N和 N. 此时整个系统恰处于平衡状态,求∠AOB的大小.
3. 若平面上的三个力F1, F2, F3作用于一点,且处于平衡状态. 已知|F1|=1N,
|F2| N, F1与 F2的夹角为45°,求:
(1) F3的大小;(2) F3与F1夹角的大小.
4.用向量方法证明两角差得余弦公式
证明:如图, 在平面直角坐标系Oxy内作单位圆O, 以x轴的非负半轴为始边作角α, β, 它们的终边与单位圆O交点分别为A, B, 则
课堂小结:
物理上力做功的实质是力在物体前进方向上的分力与物体位移距离的乘积,它的实质是向量的数量积.
1. 向量的数量积与功的关系:
2. 用向量方法解决物理问题的一般步骤是:
① 问题转化,即把物理问题转化为数学问题;
② 建立模型,即建立以向量为载体的数学模型;
③ 求解参数,即求向量的模、夹角、数量积等;
④ 回答问题,即把所得的数学结论回归到物理问题中.
2022-2023学年高一数学同步精品课堂(沪教版2020必修第二册)
第 8 章 平面向量
8.4 向量的应用 (第2课时)
8.4 向量的应用
例5 如图8-4-4,平面上A、B、C三点的坐标分别是
(2,3)、(2,0)、(1,1).已知小明在点B 处休憩,有只小狗沿着
AC所在直线来回跑动.问:其在什么位置时,离小明最近?
记 则
设D 是直线AC上随着小狗跑动而动态变化的点,则 可
写成 的形式,λ是实数.问题转化为:确定λ的值,使向量
的模| |取到最小值,此时向量
??
的终点D 即为小狗离小明最近的位置
如果D 为D0使得, , 即 ,那么向量
的模取到最小值.于是,λ要满足 ,即
= 故
从而 最终推出
D0的坐标是
因此,当其在点 时,离小明最近.
例6 用向量方法证明:
证明 如图8-4-5,建立平面直角坐标系,并设A、B是单
位圆上的任意两点,而角α与β都是顶点在原点O、始边为 x 轴
正半轴的角,其终边分别落在AB与OB上.考虑向量
我们要求出 (的余弦).注意到交换α与β不影响要
证明的公式,可以假设从 旋转到 的最小正角就是 .这
个角与角α-β有相同的始边与终边,于是
又由于| =| |=1,我们得到
另一方面,用向量的坐标表示来计算数量积,我们有
综上所述,
例7 将质量为20kg的物体用两根绳子悬挂起来,如图
8-4-6(1),两根绳子与铅垂线的夹角分别为45°与30°.求
它们分别提供的拉力的大小.(结果精确到0.1N)
解 设两根绳子的拉力分别是 与 ,则它们的合力
与物体的重力大小相等、方向相反,即 是垂直向上、模为
20g(N)的向量,这里g≈9.8(m/s2)是重力加速度.
以 的公共作用点为原点,以 为 y 的正半轴,
建立平面直角坐标系,如图8-4-6(2)所示.
令 则
因为 所以
解得
综上所述,这两根绳子所提供的拉力分别约为101.5N和
143.5N.
1. 问题转化,即把物理问题转化为数学问题;
用向量方法解决物理学中的相关问题的步骤:
2. 建立模型,即建立以向量为载体的数学模型;
3. 求解参数,即求向量的模、夹角、数量积等;
4. 回答问题,即把所得的数学结论回归到物理问题中.
课本练习
练习8.4(2)
1.已知两个力(单位:: 的夹角为60°,其中 (2.0).
某质点在这两个力的共同作用下,由点A(1,1)移动至点b(6,6)(单位:m).
(1)求 ;
(2)求 与 的合力对质点所做的功.
2.已知平面上三点A、B、C的坐标分别是(1,7)、(2,2)、(0,1),P为直
线AC上的一动点.问:P在什么位置时, 取到最小值?
随堂检测
1. 一物体在力F的作用下,由点A(20, 15)移动到点B(7, 0). 已知F=(4, -5),求F对该物体所做的功.
2. 如图,一滑轮组中有两个定滑轮A,B,在从连接点O出发的三根绳的端点处,挂着3个重物,它们所受的重力分别为4 N,4 N和 N. 此时整个系统恰处于平衡状态,求∠AOB的大小.
3. 若平面上的三个力F1, F2, F3作用于一点,且处于平衡状态. 已知|F1|=1N,
|F2| N, F1与 F2的夹角为45°,求:
(1) F3的大小;(2) F3与F1夹角的大小.
4.用向量方法证明两角差得余弦公式
证明:如图, 在平面直角坐标系Oxy内作单位圆O, 以x轴的非负半轴为始边作角α, β, 它们的终边与单位圆O交点分别为A, B, 则
课堂小结:
物理上力做功的实质是力在物体前进方向上的分力与物体位移距离的乘积,它的实质是向量的数量积.
1. 向量的数量积与功的关系:
2. 用向量方法解决物理问题的一般步骤是:
① 问题转化,即把物理问题转化为数学问题;
② 建立模型,即建立以向量为载体的数学模型;
③ 求解参数,即求向量的模、夹角、数量积等;
④ 回答问题,即把所得的数学结论回归到物理问题中.
