2023年中考数学第三轮冲刺--平面直角坐标系(含答案)
文档属性
| 名称 | 2023年中考数学第三轮冲刺--平面直角坐标系(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 449.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-04 22:41:50 | ||
图片预览


文档简介
2023年初中数学第三轮冲刺--平面直角坐标系
一、单选题
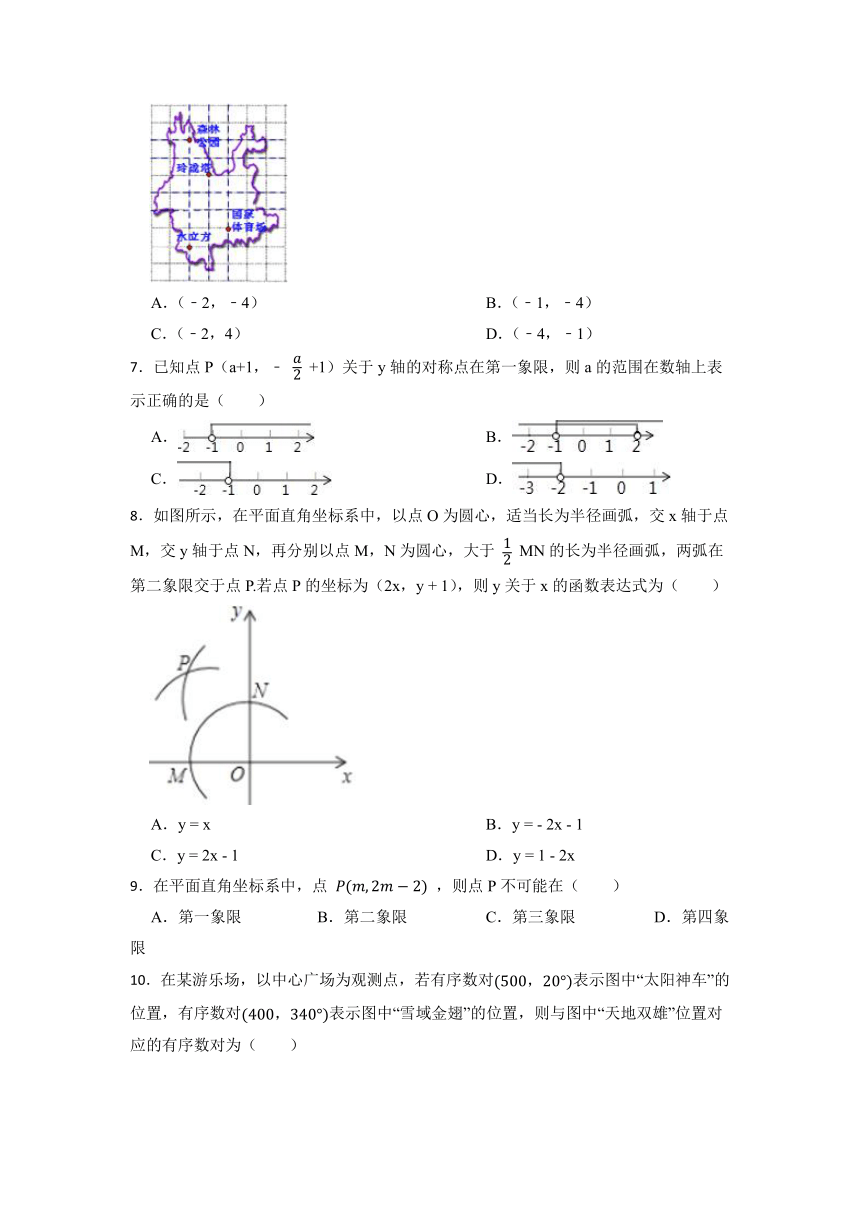
1.如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时的点为P1,第2次碰到矩形的边时的点为P2,…,第n次碰到矩形的边时的点为Pn,则点P2015的坐标是( )
A.(1,4) B.(3,0) C.(7,4) D.(5,0)
2.定义:直线l1与l2相交于点O,对于平面内任意一点M,点M到直线l1、l2的距离分别为p、q,则称有序实数对(p,q)是点M的“距离坐标”,根据上述定义,“距离坐标”是(1,2)的点的个数是( )
A.2 B.3 C.4 D.5
3.点A(-4,-5),点B(-6,-5),则AB等于( )
A.4 B.2 C.5 D.3
4.如图,已知棋子“卒”的坐标为 (﹣2,3),棋子“马”的坐标为(1,3),则棋子“炮”的坐标为( )
A.(2,2) B.(4,1) C.(﹣2,2) D.(4,2)
5.已知点M向左平移3个单位长度后的坐标为 ,则点M原来的坐标是
A. B. C. D.
6.我市为了促进全民健身,举办“健步走”活动,朝阳区活动场地位于奥林匹克公园(路线:森林公园﹣玲珑塔﹣国家体育场﹣水立方).如图,体育局的工作人员在奥林匹克公园设计图上设定玲珑塔的坐标为(﹣1,0),森林公园的坐标为(﹣2,2),则终点水立方的坐标为( )
A.(﹣2,﹣4) B.(﹣1,﹣4)
C.(﹣2,4) D.(﹣4,﹣1)
7.已知点P(a+1,﹣ +1)关于y轴的对称点在第一象限,则a的范围在数轴上表示正确的是( )
A. B.
C. D.
8.如图所示,在平面直角坐标系中,以点O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于 MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2x,y + 1),则y关于x的函数表达式为( )
A.y = x B.y = - 2x - 1
C.y = 2x - 1 D.y = 1 - 2x
9.在平面直角坐标系中,点 ,则点P不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.在某游乐场,以中心广场为观测点,若有序数对表示图中“太阳神车”的位置,有序数对表示图中“雪域金翅”的位置,则与图中“天地双雄”位置对应的有序数对为( )
A. B.
C. D.
11.抛物线y=x2﹣9与x轴交于A、B两点,点P在函数y= 的图象上,若△PAB为直角三角形,则满足条件的点P的个数为( )
A.2个 B.3个 C.4个 D.6个
12.在平面直角坐标系中,点A(﹣2022,2022)位于哪个象限?( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
13.经过两点A(2,3)、B(-4,3)作直线AB,则直线AB( )
A.平行于x轴 B.平行于y轴 C.经过原点 D.无法确定
14.已知点P(x,y)的坐标满足|x|=3, =2,且xy<0,则点P的坐标是( )
A. B. C. D.
15.在平面直角坐标系xOy中,已知点P(2,2),点Q在y轴上,△PQO是等腰三角形,则满足条件的点Q共有( )
A.5个 B.4个 C.3个 D.2个
二、填空题
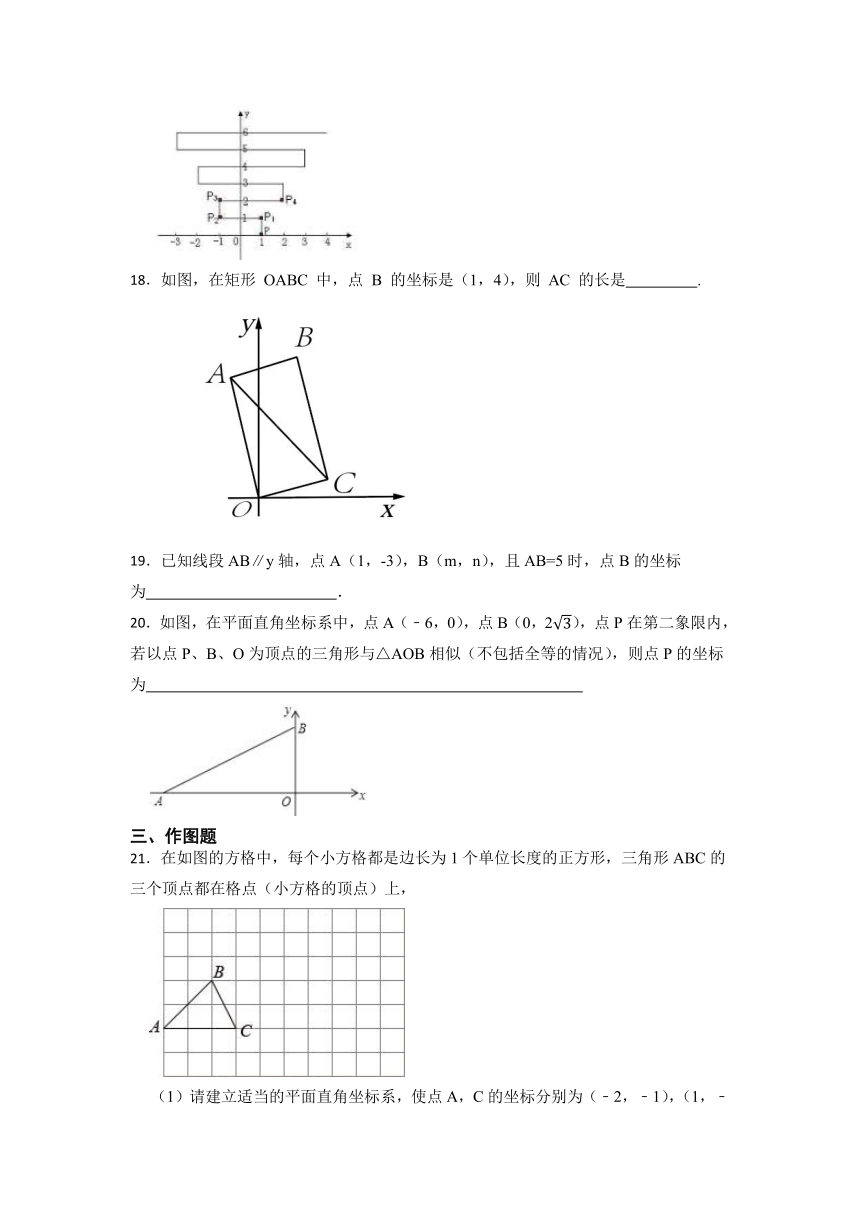
16.已知点 , 点的坐标为 ,直线 轴,则a的值是 .
17.如下图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位…,依此规律跳动下去,点P第2019次跳动至点P2019的坐标是 .
18.如图,在矩形 OABC 中,点 B 的坐标是(1,4),则 AC 的长是 .
19.已知线段AB∥y轴,点A(1,-3),B(m,n),且AB=5时,点B的坐标为 .
20.如图,在平面直角坐标系中,点A(﹣6,0),点B(0,2),点P在第二象限内,若以点P、B、O为顶点的三角形与△AOB相似(不包括全等的情况),则点P的坐标为
三、作图题
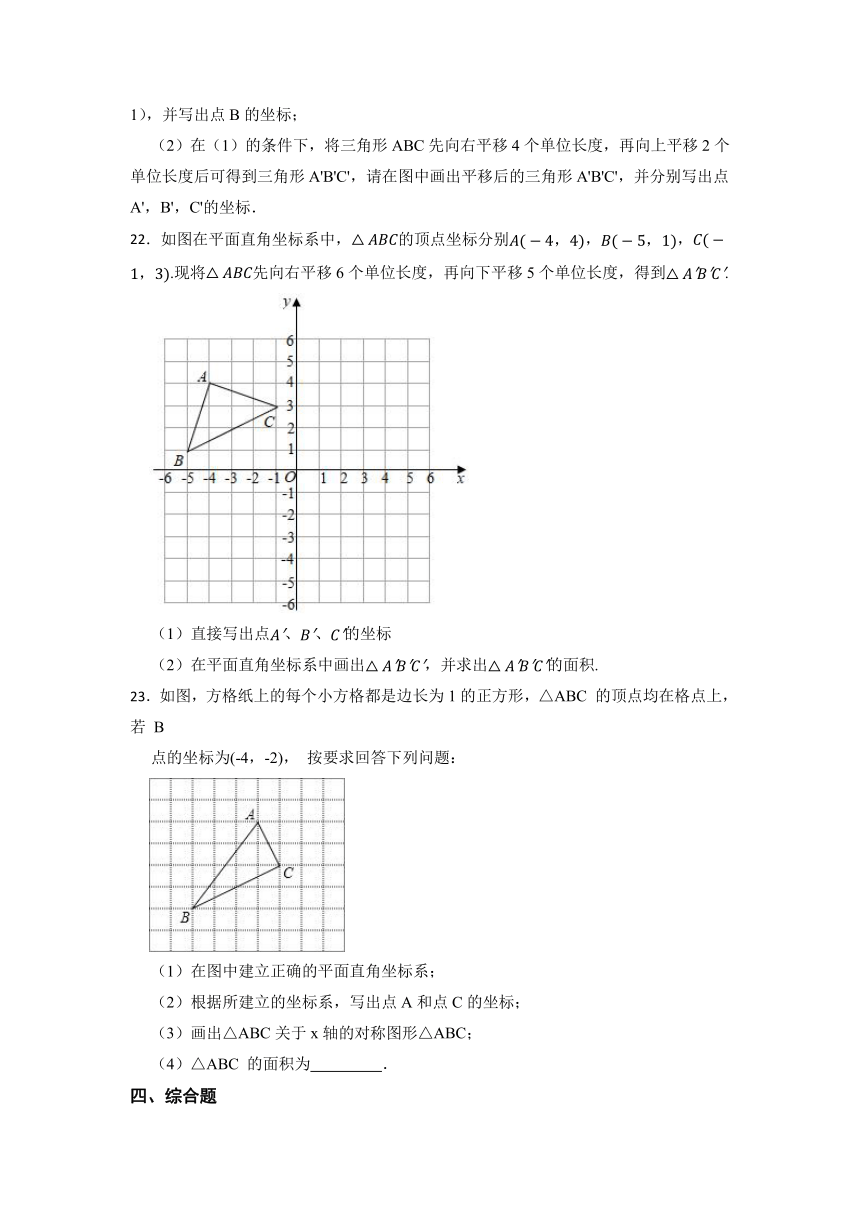
21.在如图的方格中,每个小方格都是边长为1个单位长度的正方形,三角形ABC的三个顶点都在格点(小方格的顶点)上,
(1)请建立适当的平面直角坐标系,使点A,C的坐标分别为(﹣2,﹣1),(1,﹣1),并写出点B的坐标;
(2)在(1)的条件下,将三角形ABC先向右平移4个单位长度,再向上平移2个单位长度后可得到三角形A'B'C',请在图中画出平移后的三角形A'B'C',并分别写出点A',B',C'的坐标.
22.如图在平面直角坐标系中,的顶点坐标分别,,.现将先向右平移6个单位长度,再向下平移5个单位长度,得到.
(1)直接写出点、、的坐标
(2)在平面直角坐标系中画出,并求出的面积.
23.如图,方格纸上的每个小方格都是边长为1的正方形,△ABC 的顶点均在格点上,若 B
点的坐标为(-4,-2), 按要求回答下列问题:
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出点A和点C的坐标;
(3)画出△ABC关于x轴的对称图形△ABC;
(4)△ABC 的面积为 .
四、综合题
24.如图是某学校的平面示意图,已知旗杆的位置是(﹣2,3),实验室的位置是(1,4)
(1)根据所给条件在图中建立适当的平面直角坐标系;
(2)用坐标表示位置:食堂 ,图书馆 .
(3)已知办公楼的位置是(﹣2,1),教学楼的位置是(2,2),在图中标出办公楼和教学楼的位置;
25.如图,在边长为1的正方形组成的网格中建立直角坐标系,的顶点均在格点上,点O为原点,点A、B的坐标分别是、.
(1)将向下平移2个单位后得到,则点的坐标为 ;
(2)将绕点O逆时针旋转后得到,请在图中作出;
(3)在(2)的旋转过程中,求线段扫过的图形的面积.
26.如图,在平面直角坐标系中,三角形的三个顶点坐标分别为,点的坐标是,现将三角形平移,使点A平移到点处,分别是B,C的对应点.
(1)根据题意,画出平移后的三角形(不写画法),并直接写出的坐标;
(2)求三角形的面积;
(3)若将C点向右平移个单位长度到点D,使得三角形的面积等于3,直接写出m的值.
27.已知点在平面直角坐标系内.
(1)若点在第四象限,求的取值范围;
(2)若点在坐标轴上,求的值.
28.对于平面直角坐标系xOy中的图形W和点P,给出如下定义:F为图形W上任意一点,将P,F两点间距离的最小值记为m,最大值记为M,称M与m的差为点P到图形W的“差距离”,记作d(P,W),即d(P,W)=M-m,已知点A(2,1),B(-2,1)
(1)求d(O,AB);
(2)点C为直线y=1上的一个动点,当d(C,AB)=1时,点C的横坐标是 ;
(3)点D为函数y=x+b(-2≤x≤2)图象上的任意一点,当d(D,AB)≤2时,直接写出b的取值范围.
答案解析部分
1.【答案】A
2.【答案】C
3.【答案】B
4.【答案】D
5.【答案】B
6.【答案】A
7.【答案】C
8.【答案】B
9.【答案】B
10.【答案】B
11.【答案】D
12.【答案】B
13.【答案】A
14.【答案】D
15.【答案】B
16.【答案】3
17.【答案】(-505,1010).
18.【答案】
19.【答案】(1,2)或(1,-8)
20.【答案】(﹣,)或(﹣2,2)或(﹣,)
21.【答案】(1)解:平面直角坐标系如图所示:B(0,1).
(2)解:△A′B′C′如图所示.A′(2,1),B′(4,3),C′(5,1).
22.【答案】(1)解:由题意知,点,,;
(2)解:如图所示,△即为所求.
△的面积为.
23.【答案】(1)解:如图所示:
(2)解:点 A(﹣1,2),点 C(0,0)
(3)解:如图所示:△A′B′C′即为所求
(4)5
24.【答案】(1)解:如图,以大门为坐标原点建立坐标系,
则满足旗杆的位置是(﹣2,3),实验室的位置是(1,4)
(2)(-5,5);(2,5)
(3)解:根据办公楼的位置是(﹣2,1),教学楼的位置是(2,2),描点如图所示
25.【答案】(1)(1,1)
(2)解:作出点A、B旋转后的对应点、,顺次连接,则即为所求,如图所示:
(3)解:由图可知:,
∴扫过的面积为:.
26.【答案】(1)解:如图所示,三角形A'B'C'即为所求,点B'的坐标为(-2,5);
(2)解:三角形ABC的面积=×6×3=9;
(3)解:C点向右平移m(m>0)个单位长度到点D(-1+m,2),
∴点D到AB的距离为|-1+m-2|,
∵三角形ABD的面积等于3,
∴×6×|-1+m-2|=3,
解得m=4或2.
27.【答案】(1)解:根据题意,若点在第四象限,
可得,
解得
(2)解:根据题意,若点在坐标轴上,
当点在轴上时,可有,解得,
当点在轴上,可有,解得,
综上所述,的值为2或5.
28.【答案】(1)解:如图1中, ∵A(2,1),B(-2,1), ∴AB∥x轴,
∴点O到线段AB的最小距离为1,最大距离为 ,
∴d(O,AB)= -1.
(2) 或
(3)解:如图3中, 当b=6时,线段EF:y=x+6(-2≤x≤2)上任意一点D,满足d(D,AB)≤2,
当b=-4时,线段E′F′:y=x-4(-2≤x≤2)上任意一点D′,满足d(D′,AB)≤2,
观察图象可知:当b≥6或b≤-4时,函数y=x+b(-2≤x≤2)图象上的任意一点,满足d(D,AB)≤2.
一、单选题
1.如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时的点为P1,第2次碰到矩形的边时的点为P2,…,第n次碰到矩形的边时的点为Pn,则点P2015的坐标是( )
A.(1,4) B.(3,0) C.(7,4) D.(5,0)
2.定义:直线l1与l2相交于点O,对于平面内任意一点M,点M到直线l1、l2的距离分别为p、q,则称有序实数对(p,q)是点M的“距离坐标”,根据上述定义,“距离坐标”是(1,2)的点的个数是( )
A.2 B.3 C.4 D.5
3.点A(-4,-5),点B(-6,-5),则AB等于( )
A.4 B.2 C.5 D.3
4.如图,已知棋子“卒”的坐标为 (﹣2,3),棋子“马”的坐标为(1,3),则棋子“炮”的坐标为( )
A.(2,2) B.(4,1) C.(﹣2,2) D.(4,2)
5.已知点M向左平移3个单位长度后的坐标为 ,则点M原来的坐标是
A. B. C. D.
6.我市为了促进全民健身,举办“健步走”活动,朝阳区活动场地位于奥林匹克公园(路线:森林公园﹣玲珑塔﹣国家体育场﹣水立方).如图,体育局的工作人员在奥林匹克公园设计图上设定玲珑塔的坐标为(﹣1,0),森林公园的坐标为(﹣2,2),则终点水立方的坐标为( )
A.(﹣2,﹣4) B.(﹣1,﹣4)
C.(﹣2,4) D.(﹣4,﹣1)
7.已知点P(a+1,﹣ +1)关于y轴的对称点在第一象限,则a的范围在数轴上表示正确的是( )
A. B.
C. D.
8.如图所示,在平面直角坐标系中,以点O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于 MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2x,y + 1),则y关于x的函数表达式为( )
A.y = x B.y = - 2x - 1
C.y = 2x - 1 D.y = 1 - 2x
9.在平面直角坐标系中,点 ,则点P不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.在某游乐场,以中心广场为观测点,若有序数对表示图中“太阳神车”的位置,有序数对表示图中“雪域金翅”的位置,则与图中“天地双雄”位置对应的有序数对为( )
A. B.
C. D.
11.抛物线y=x2﹣9与x轴交于A、B两点,点P在函数y= 的图象上,若△PAB为直角三角形,则满足条件的点P的个数为( )
A.2个 B.3个 C.4个 D.6个
12.在平面直角坐标系中,点A(﹣2022,2022)位于哪个象限?( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
13.经过两点A(2,3)、B(-4,3)作直线AB,则直线AB( )
A.平行于x轴 B.平行于y轴 C.经过原点 D.无法确定
14.已知点P(x,y)的坐标满足|x|=3, =2,且xy<0,则点P的坐标是( )
A. B. C. D.
15.在平面直角坐标系xOy中,已知点P(2,2),点Q在y轴上,△PQO是等腰三角形,则满足条件的点Q共有( )
A.5个 B.4个 C.3个 D.2个
二、填空题
16.已知点 , 点的坐标为 ,直线 轴,则a的值是 .
17.如下图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位…,依此规律跳动下去,点P第2019次跳动至点P2019的坐标是 .
18.如图,在矩形 OABC 中,点 B 的坐标是(1,4),则 AC 的长是 .
19.已知线段AB∥y轴,点A(1,-3),B(m,n),且AB=5时,点B的坐标为 .
20.如图,在平面直角坐标系中,点A(﹣6,0),点B(0,2),点P在第二象限内,若以点P、B、O为顶点的三角形与△AOB相似(不包括全等的情况),则点P的坐标为
三、作图题
21.在如图的方格中,每个小方格都是边长为1个单位长度的正方形,三角形ABC的三个顶点都在格点(小方格的顶点)上,
(1)请建立适当的平面直角坐标系,使点A,C的坐标分别为(﹣2,﹣1),(1,﹣1),并写出点B的坐标;
(2)在(1)的条件下,将三角形ABC先向右平移4个单位长度,再向上平移2个单位长度后可得到三角形A'B'C',请在图中画出平移后的三角形A'B'C',并分别写出点A',B',C'的坐标.
22.如图在平面直角坐标系中,的顶点坐标分别,,.现将先向右平移6个单位长度,再向下平移5个单位长度,得到.
(1)直接写出点、、的坐标
(2)在平面直角坐标系中画出,并求出的面积.
23.如图,方格纸上的每个小方格都是边长为1的正方形,△ABC 的顶点均在格点上,若 B
点的坐标为(-4,-2), 按要求回答下列问题:
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出点A和点C的坐标;
(3)画出△ABC关于x轴的对称图形△ABC;
(4)△ABC 的面积为 .
四、综合题
24.如图是某学校的平面示意图,已知旗杆的位置是(﹣2,3),实验室的位置是(1,4)
(1)根据所给条件在图中建立适当的平面直角坐标系;
(2)用坐标表示位置:食堂 ,图书馆 .
(3)已知办公楼的位置是(﹣2,1),教学楼的位置是(2,2),在图中标出办公楼和教学楼的位置;
25.如图,在边长为1的正方形组成的网格中建立直角坐标系,的顶点均在格点上,点O为原点,点A、B的坐标分别是、.
(1)将向下平移2个单位后得到,则点的坐标为 ;
(2)将绕点O逆时针旋转后得到,请在图中作出;
(3)在(2)的旋转过程中,求线段扫过的图形的面积.
26.如图,在平面直角坐标系中,三角形的三个顶点坐标分别为,点的坐标是,现将三角形平移,使点A平移到点处,分别是B,C的对应点.
(1)根据题意,画出平移后的三角形(不写画法),并直接写出的坐标;
(2)求三角形的面积;
(3)若将C点向右平移个单位长度到点D,使得三角形的面积等于3,直接写出m的值.
27.已知点在平面直角坐标系内.
(1)若点在第四象限,求的取值范围;
(2)若点在坐标轴上,求的值.
28.对于平面直角坐标系xOy中的图形W和点P,给出如下定义:F为图形W上任意一点,将P,F两点间距离的最小值记为m,最大值记为M,称M与m的差为点P到图形W的“差距离”,记作d(P,W),即d(P,W)=M-m,已知点A(2,1),B(-2,1)
(1)求d(O,AB);
(2)点C为直线y=1上的一个动点,当d(C,AB)=1时,点C的横坐标是 ;
(3)点D为函数y=x+b(-2≤x≤2)图象上的任意一点,当d(D,AB)≤2时,直接写出b的取值范围.
答案解析部分
1.【答案】A
2.【答案】C
3.【答案】B
4.【答案】D
5.【答案】B
6.【答案】A
7.【答案】C
8.【答案】B
9.【答案】B
10.【答案】B
11.【答案】D
12.【答案】B
13.【答案】A
14.【答案】D
15.【答案】B
16.【答案】3
17.【答案】(-505,1010).
18.【答案】
19.【答案】(1,2)或(1,-8)
20.【答案】(﹣,)或(﹣2,2)或(﹣,)
21.【答案】(1)解:平面直角坐标系如图所示:B(0,1).
(2)解:△A′B′C′如图所示.A′(2,1),B′(4,3),C′(5,1).
22.【答案】(1)解:由题意知,点,,;
(2)解:如图所示,△即为所求.
△的面积为.
23.【答案】(1)解:如图所示:
(2)解:点 A(﹣1,2),点 C(0,0)
(3)解:如图所示:△A′B′C′即为所求
(4)5
24.【答案】(1)解:如图,以大门为坐标原点建立坐标系,
则满足旗杆的位置是(﹣2,3),实验室的位置是(1,4)
(2)(-5,5);(2,5)
(3)解:根据办公楼的位置是(﹣2,1),教学楼的位置是(2,2),描点如图所示
25.【答案】(1)(1,1)
(2)解:作出点A、B旋转后的对应点、,顺次连接,则即为所求,如图所示:
(3)解:由图可知:,
∴扫过的面积为:.
26.【答案】(1)解:如图所示,三角形A'B'C'即为所求,点B'的坐标为(-2,5);
(2)解:三角形ABC的面积=×6×3=9;
(3)解:C点向右平移m(m>0)个单位长度到点D(-1+m,2),
∴点D到AB的距离为|-1+m-2|,
∵三角形ABD的面积等于3,
∴×6×|-1+m-2|=3,
解得m=4或2.
27.【答案】(1)解:根据题意,若点在第四象限,
可得,
解得
(2)解:根据题意,若点在坐标轴上,
当点在轴上时,可有,解得,
当点在轴上,可有,解得,
综上所述,的值为2或5.
28.【答案】(1)解:如图1中, ∵A(2,1),B(-2,1), ∴AB∥x轴,
∴点O到线段AB的最小距离为1,最大距离为 ,
∴d(O,AB)= -1.
(2) 或
(3)解:如图3中, 当b=6时,线段EF:y=x+6(-2≤x≤2)上任意一点D,满足d(D,AB)≤2,
当b=-4时,线段E′F′:y=x-4(-2≤x≤2)上任意一点D′,满足d(D′,AB)≤2,
观察图象可知:当b≥6或b≤-4时,函数y=x+b(-2≤x≤2)图象上的任意一点,满足d(D,AB)≤2.
同课章节目录
