多边形的内角和与外角和[下学期]
图片预览





文档简介
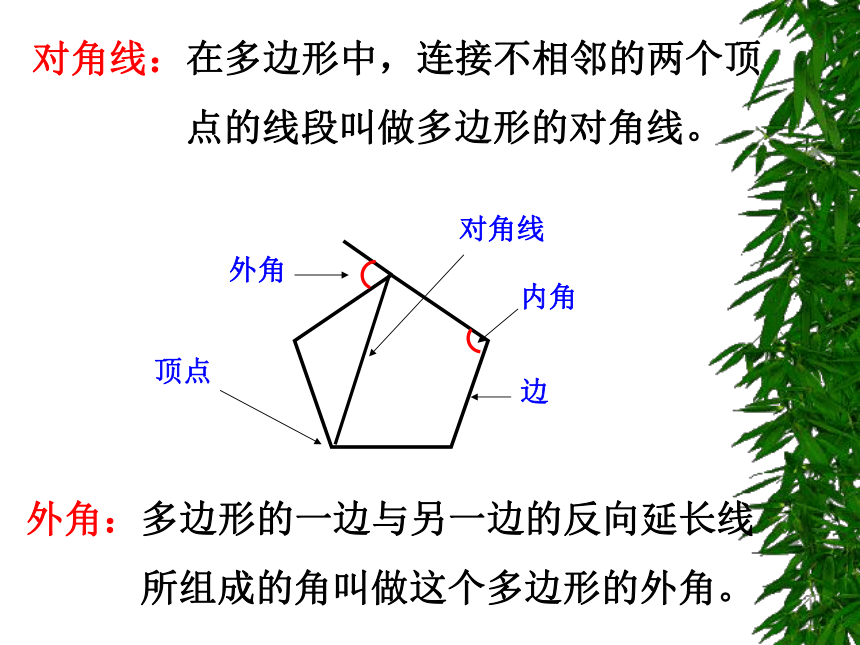
课件18张PPT。探索多边形内角和与外角和 在平面内,由三条不在同一直线上的线段首尾顺次连接组成封闭图形叫做三角形。 在平面内,由四条不在同一直线上的线段首尾顺次连接组成的封闭图形叫做四边形。 在平面内,由5条不在同一直线上的线段首尾顺次连接组成的封闭图形叫做五边形。多 边 形 在平面内,由若干不在同一直线上的线段首尾顺次连接组成的封闭图形叫做多边形。顶点内角边外角对角线对角线:在多边形中,连接不相邻的两个顶
点的线段叫做多边形的对角线。外角:多边形的一边与另一边的反向延长线
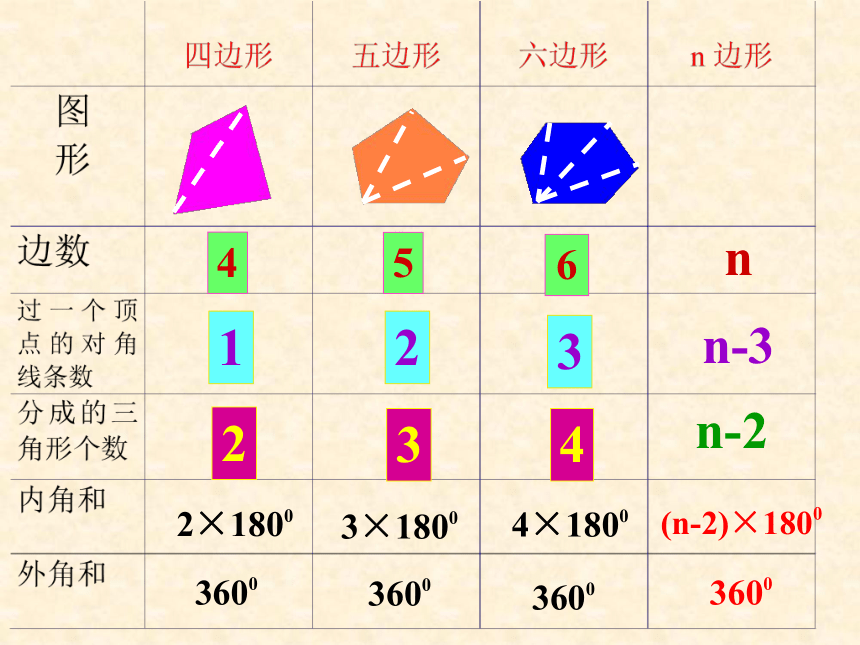
所组成的角叫做这个多边形的外角。nn-3n-23×18004×1800(n-2)×18001232344562×18003600360036003600答:15边形的内角和是23400例解:求15边形内角和的度数。 多边形的内角和n边形的内角和为(n-2)×1800(n-2)×1800=(15-2)×1800= 23400巩固练习一:1、七边形内角和为( )900°2、十边形内角和为( )1440°3、十七边形内角和为( )2700°4、二十边形内角和为( )3240°5、八边形内角和为( )1080°6、多边形每增加一边,内角和相应增加_____.
360°例:已知一个多边形的内角和
是1440O,求这个多边形的边数。解:设这个多边形为n边形。(n-2)×180° =1440°n-2=1440°÷180°n-2=8n=10答:这个多边形为十边形。巩固练习二:1、多边形内角和为1260°则它是
( )边形。2、多边形内角和为1080°则它是
( )边形。 3、多边形内角和为1800°则它是
( )边形。九八十二例:一 个多边形的每一个内角都是120°,求这个多边形的边数。解:设这个多边形的边数为n。n×120°=(n-2)×180 °120 ° n= 180 ° n-360 °-60 ° n= -360 °n=6答:这个多边形的边数为6。1、一 个多边形的每一个内角都是150°,则这个多边形的边数为_____.2、一 个多边形的每一个外角都是45°,则这个多边形的边数为______.3、一 个多边形的边数为10,则每一个内角的度数为______,外角的度数是______.128144°36°巩固练习三: 多边形的外角和n边形的外角和为3600例1:一个多边形的内角和等 于它的外角和的3倍,它是几边形?解:设这个多边形的边数为n。(n-2)×180 ° =360°×3180°n-360°=1080°180°n=1440°n=8答:它是八边形.思考:1、一个多边形的每个外角等于与它相邻的内角,这个多边形是几边形?4、若两个多边形的边数相差1,则它们的内角和、外角和分别有什么异同? 一个多边形除了一个内角所
有的内角和为1240 °求这个多
边形的边数及缺少的内角的度数? 在四边形的内角中,最多能有几个钝角?最多能有几个锐角?想一想: 特点:它们的边( )
它们的角( )都相等都相等定义:在平面内,内角都相等,边都
相等的多边形叫正多边形议一议:1、一个多边形的边相等,它的内角一定相等吗?2、一个多边形的内角都相等,它的边一定相等吗?1、每个内角都为144°的多边形为( )边形。
2、每个内角都为140°的多边形为( )边形。
3、每个外角都为30°的多边形为( )边形。
4、每个外角都为36°的多边形为( )边形。
5、正八边形的内角为( ),外角为( )。
6、正十二边形的内角为( ),外角为( )。练习三:十九十二十135°45°150°30°1、一个十边形的每一个内角都相等,
那么这个十边形的每一外角等于( )
A、144°B、 72 ° C、 36° D 、18°
2、一个多边形每一个外角都等于45°,
则这个多边形的内角和等于( )
A、 720° B、 675° C、 1080°
D、945°练习四:CC再见
点的线段叫做多边形的对角线。外角:多边形的一边与另一边的反向延长线
所组成的角叫做这个多边形的外角。nn-3n-23×18004×1800(n-2)×18001232344562×18003600360036003600答:15边形的内角和是23400例解:求15边形内角和的度数。 多边形的内角和n边形的内角和为(n-2)×1800(n-2)×1800=(15-2)×1800= 23400巩固练习一:1、七边形内角和为( )900°2、十边形内角和为( )1440°3、十七边形内角和为( )2700°4、二十边形内角和为( )3240°5、八边形内角和为( )1080°6、多边形每增加一边,内角和相应增加_____.
360°例:已知一个多边形的内角和
是1440O,求这个多边形的边数。解:设这个多边形为n边形。(n-2)×180° =1440°n-2=1440°÷180°n-2=8n=10答:这个多边形为十边形。巩固练习二:1、多边形内角和为1260°则它是
( )边形。2、多边形内角和为1080°则它是
( )边形。 3、多边形内角和为1800°则它是
( )边形。九八十二例:一 个多边形的每一个内角都是120°,求这个多边形的边数。解:设这个多边形的边数为n。n×120°=(n-2)×180 °120 ° n= 180 ° n-360 °-60 ° n= -360 °n=6答:这个多边形的边数为6。1、一 个多边形的每一个内角都是150°,则这个多边形的边数为_____.2、一 个多边形的每一个外角都是45°,则这个多边形的边数为______.3、一 个多边形的边数为10,则每一个内角的度数为______,外角的度数是______.128144°36°巩固练习三: 多边形的外角和n边形的外角和为3600例1:一个多边形的内角和等 于它的外角和的3倍,它是几边形?解:设这个多边形的边数为n。(n-2)×180 ° =360°×3180°n-360°=1080°180°n=1440°n=8答:它是八边形.思考:1、一个多边形的每个外角等于与它相邻的内角,这个多边形是几边形?4、若两个多边形的边数相差1,则它们的内角和、外角和分别有什么异同? 一个多边形除了一个内角所
有的内角和为1240 °求这个多
边形的边数及缺少的内角的度数? 在四边形的内角中,最多能有几个钝角?最多能有几个锐角?想一想: 特点:它们的边( )
它们的角( )都相等都相等定义:在平面内,内角都相等,边都
相等的多边形叫正多边形议一议:1、一个多边形的边相等,它的内角一定相等吗?2、一个多边形的内角都相等,它的边一定相等吗?1、每个内角都为144°的多边形为( )边形。
2、每个内角都为140°的多边形为( )边形。
3、每个外角都为30°的多边形为( )边形。
4、每个外角都为36°的多边形为( )边形。
5、正八边形的内角为( ),外角为( )。
6、正十二边形的内角为( ),外角为( )。练习三:十九十二十135°45°150°30°1、一个十边形的每一个内角都相等,
那么这个十边形的每一外角等于( )
A、144°B、 72 ° C、 36° D 、18°
2、一个多边形每一个外角都等于45°,
则这个多边形的内角和等于( )
A、 720° B、 675° C、 1080°
D、945°练习四:CC再见
