多边形的内角和[下学期]
图片预览


文档简介
课件17张PPT。§8.3 多边形的内角和与外角和问题情境
自主探究
知识反思
归纳小结深圳市宝安中学 曾伟茂教学目标:
1.了解多边形的有关概念;
2.掌握多边形的内角和计算公式;
3.会利用多边形的内角和公式进行计算 ;
4. 培养学生自主探究和实际操作能力;
5.渗透用类比和转化的数学思想解决问题,培养学生由具体到抽象的归纳概括能力。
教学重点:多边形内角和公式的探究与运用。
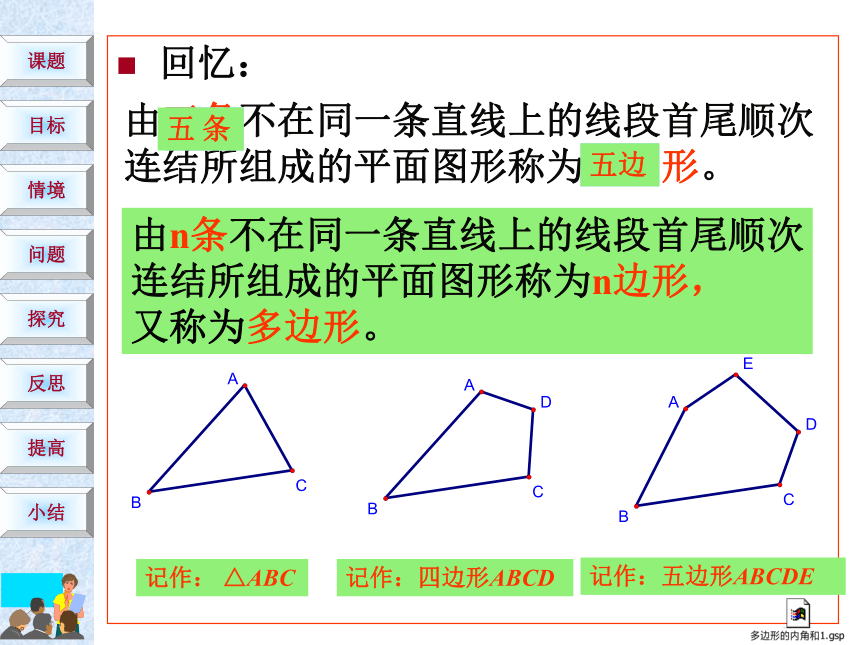
教学难点:多边形内角和公式的探究与运用。回忆:由三条不在同一条直线上的线段首尾顺次
连结所组成的平面图形称为三角形。四条四边五 条五边由n条不在同一条直线上的线段首尾顺次
连结所组成的平面图形称为n边形,
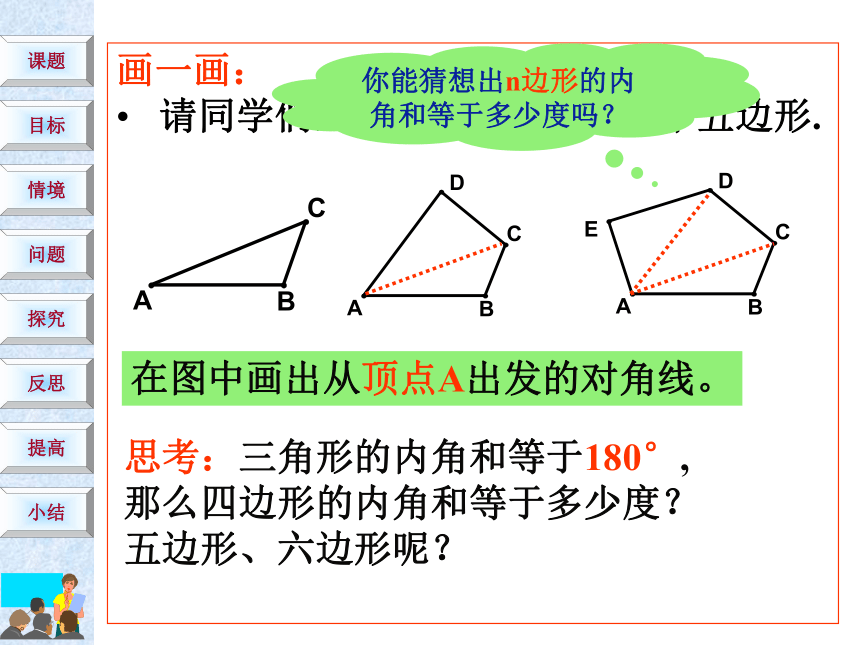
又称为多边形。记作: △ABC记作:四边形ABCD记作:五边形ABCDE画一画:
请同学们画出一个四边形和一个五边形.在图中画出从顶点A出发的对角线。思考:三角形的内角和等于180°,
那么四边形的内角和等于多少度?
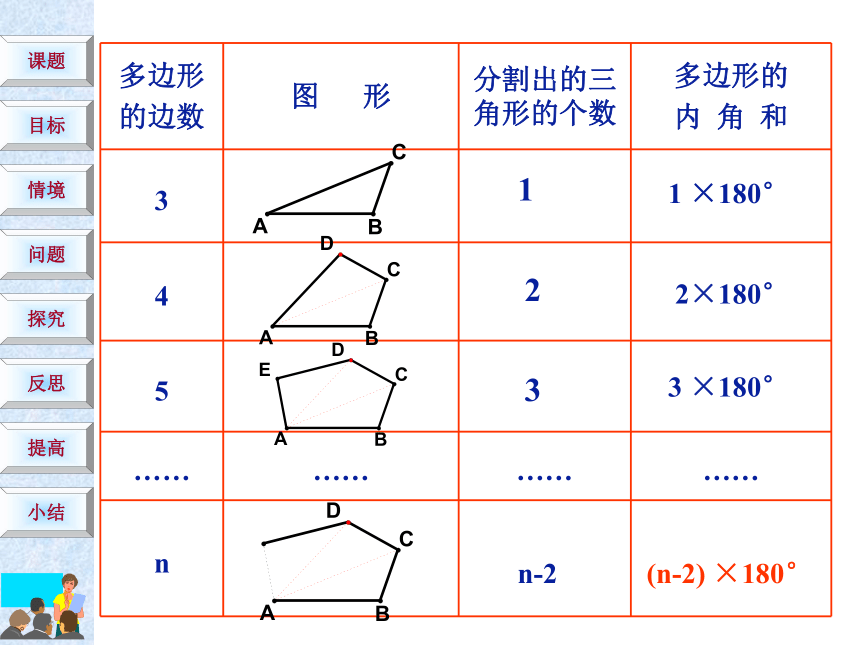
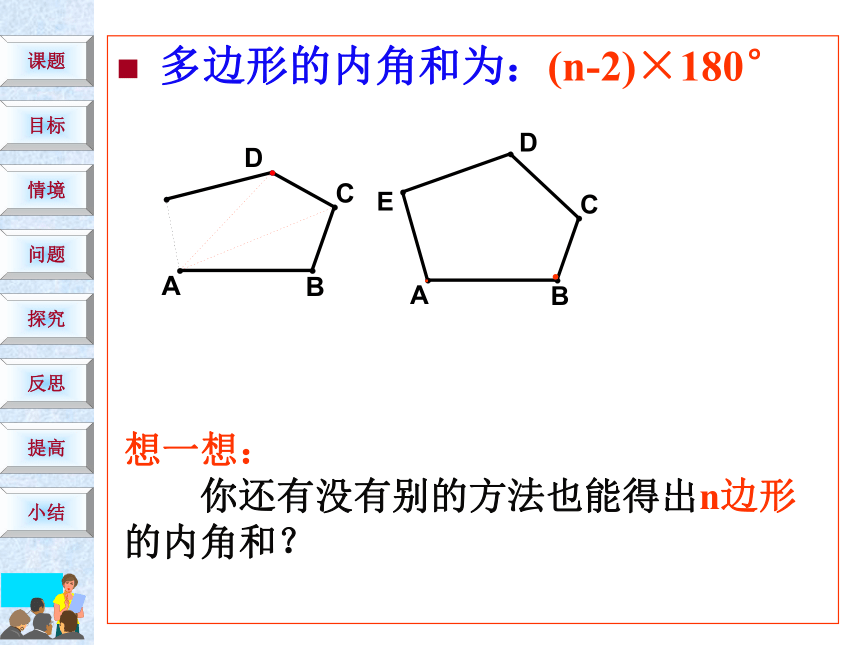
五边形、六边形呢?你能猜想出n边形的内角和等于多少度吗?11 ×180°22×180°33 ×180°n-2(n-2) ×180°多边形的内角和为:(n-2)×180°想一想:
你还有没有别的方法也能得出n边形的内角和?..探究:从n边形的内部任取一点,过这个点与多边形的每一个顶点连结线段,你能发现什么?...探究:在n边形某一边上任取一点,过这个点与多边形的每一个顶点连结线段,你能发现什么?...多边形的内角和为:(n-2)×180°
上述推导多边形内角和公式的基本思想是什么?多边形的内角和为:(n-2)×180°
例1:求八边形的内角和。
解:(n-2)×180°
=(8-2) ×180°
=1080°[基础练习]
1、十边形的内角和是 ;如果十边形的各个内角都相等,那么它的一个内角是 。
2、一个多边形的内角和为1620°,则这个多边形的边数是 。
3、六角螺母的一个面是正六边形,这个六边形的六个内角都相等,则一个内角的度数是 。1440°144°11120°[能力提高]
1、如果一个四边形增加一边成为五边形,那么它的内角和增加 ;
2、已知一个多边形的内角和是直角的10倍,则此多边形是 边形。
3、一个多边形的内角和不可能是( )
(A) 1800 °;(B)360 °;(C)1080 °;(D) 910 °. 180°7D[能力挑战]
已知多边形的边数恰好是从一个顶点出发的对角线条数的2倍,求此多边形的边数与内角和。解:设此多边形的边数为n,
依题意得:n=2(n-3),
解得 n=6
所以,(n-2) ×180°
=(6-2) ×180°
=720°探究:在n边形外取点P,连结点P与多边形的每一个顶点,能否推出多边形的内角和呢?归纳小结
一、谈谈这节课的收获和感受:
1、 n边形的内角和:(n-2)·180o,揭示了多边形的内角和与边数的关系:当边数增加1时,内角和增加180o;n边形的内角和是180o的整数倍。 2、体会类比、归纳、概括、从具体到抽象、化未知为已知等数学思想与方法。二、作业布置:
1)阅读课本P52~55页内容
2)习题8.3第1、2题
3)探索:n边形的对角线一共多少条? .板书设计
自主探究
知识反思
归纳小结深圳市宝安中学 曾伟茂教学目标:
1.了解多边形的有关概念;
2.掌握多边形的内角和计算公式;
3.会利用多边形的内角和公式进行计算 ;
4. 培养学生自主探究和实际操作能力;
5.渗透用类比和转化的数学思想解决问题,培养学生由具体到抽象的归纳概括能力。
教学重点:多边形内角和公式的探究与运用。
教学难点:多边形内角和公式的探究与运用。回忆:由三条不在同一条直线上的线段首尾顺次
连结所组成的平面图形称为三角形。四条四边五 条五边由n条不在同一条直线上的线段首尾顺次
连结所组成的平面图形称为n边形,
又称为多边形。记作: △ABC记作:四边形ABCD记作:五边形ABCDE画一画:
请同学们画出一个四边形和一个五边形.在图中画出从顶点A出发的对角线。思考:三角形的内角和等于180°,
那么四边形的内角和等于多少度?
五边形、六边形呢?你能猜想出n边形的内角和等于多少度吗?11 ×180°22×180°33 ×180°n-2(n-2) ×180°多边形的内角和为:(n-2)×180°想一想:
你还有没有别的方法也能得出n边形的内角和?..探究:从n边形的内部任取一点,过这个点与多边形的每一个顶点连结线段,你能发现什么?...探究:在n边形某一边上任取一点,过这个点与多边形的每一个顶点连结线段,你能发现什么?...多边形的内角和为:(n-2)×180°
上述推导多边形内角和公式的基本思想是什么?多边形的内角和为:(n-2)×180°
例1:求八边形的内角和。
解:(n-2)×180°
=(8-2) ×180°
=1080°[基础练习]
1、十边形的内角和是 ;如果十边形的各个内角都相等,那么它的一个内角是 。
2、一个多边形的内角和为1620°,则这个多边形的边数是 。
3、六角螺母的一个面是正六边形,这个六边形的六个内角都相等,则一个内角的度数是 。1440°144°11120°[能力提高]
1、如果一个四边形增加一边成为五边形,那么它的内角和增加 ;
2、已知一个多边形的内角和是直角的10倍,则此多边形是 边形。
3、一个多边形的内角和不可能是( )
(A) 1800 °;(B)360 °;(C)1080 °;(D) 910 °. 180°7D[能力挑战]
已知多边形的边数恰好是从一个顶点出发的对角线条数的2倍,求此多边形的边数与内角和。解:设此多边形的边数为n,
依题意得:n=2(n-3),
解得 n=6
所以,(n-2) ×180°
=(6-2) ×180°
=720°探究:在n边形外取点P,连结点P与多边形的每一个顶点,能否推出多边形的内角和呢?归纳小结
一、谈谈这节课的收获和感受:
1、 n边形的内角和:(n-2)·180o,揭示了多边形的内角和与边数的关系:当边数增加1时,内角和增加180o;n边形的内角和是180o的整数倍。 2、体会类比、归纳、概括、从具体到抽象、化未知为已知等数学思想与方法。二、作业布置:
1)阅读课本P52~55页内容
2)习题8.3第1、2题
3)探索:n边形的对角线一共多少条? .板书设计
