三角形的三边关系[下学期]
图片预览





文档简介
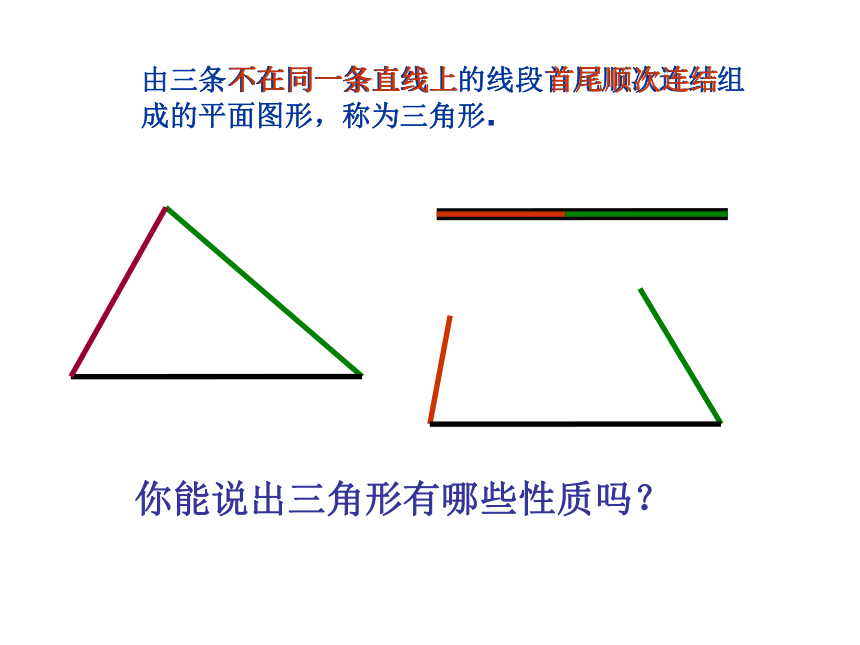
课件19张PPT。§8.2.3 三角形的三边关系三角形的三边关系??华东师大由三条不在同一条直线上的线段首尾顺次连结组成的平面图形,称为三角形.你能说出三角形有哪些性质吗?不在同一条直线上首尾顺次连结大
道草坪一.实验 准备好长度分别为:2cm,3cm,5cm,6cm的牙签
各一根,从中任取三根看都能不能摆成一个三角形?从4根中取出3根有以下几种情况:(1)2cm,3cm,5cm通过动手发现: (3) (4) 可以摆成三角形,
(1) (2) 不能摆成三角形。通过实验你能发现
构成一个三角形的三边有什么规律?发现:三角形的任何两边的和大于第三边。(2)2cm,3cm,6cm(3)2cm,5cm,6cm(4)3cm,5cm,6cm二.画一个三边分别为7cm,5cm,4cm的三角形。画法步骤:(1)先画线段AB=7cm;(2)以点A为圆心,5cm长为半径画圆弧:(3)以点B为圆心,4cm长为半径画圆弧,
两弧相交于点C;(4)连接AC、BC 。试一试:你能用类似的方法画出三边长分别为:
9cm,4cm,4cm的三角形吗?例一. 有两根长度分别为5cm和8cm的木棒,现在再取
一根木棒与它们摆成一个三角形,你说第三根要多长呢?用长度为3cm的木棒行吗?为什么?用长度为14cm的木棒呢?已知三角形两边的长度,第三边长度范围是:如果告诉你:
三角形两边的长度,
第三边长度的范围你能确定吗?大于这两边的差,小于这两边的和。三. 三角形的稳定性1.三角形的三边确定了三角形的
形状和大小就完全确定了;
这个性质叫做三角形的稳定性。2.四边形有这个性质吗?3.你能举出三角形的稳定性在生产、
生活中应用的例子吗?只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形.下列长度的各组线段能否组成一个三角形?
(1)15cm、10cm、7cm (2) 4cm、5cm、10cm
(3) 3cm、8cm、5cm (4) 4cm、5cm、6cm练一练只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形.下列长度的各组线段能否组成一个三角形?
(1)15cm、10cm、7cm (2) 4cm、5cm、10cm
(3) 3cm、8cm、5cm (4) 4cm、5cm、6cm (2) 因为4cm+5cm<10cm,
所以这三条线段不能组成一个三角形. (3) 因为3cm+5cm=8cm,
所以这三条线段不能组成一个三角形.练一练 (4) 因为4cm+5cm>6cm,
所以这三条线段能组成一个三角形.1、已知两条线段的长分别是3cm、5cm ,
要想拼成一个三角形,问第三条线段a应
取的范围是多少? 试一试: 2、已知两条线段的长分别是3cm、5cm ,
要想拼成一个三角形,且第三条线段a的
长为奇数,问第三条线段应取多少长? 2cm 你可以画出几个符合条件的等腰三角形?做一做:1、已知两条边长分别为3cm、5cm,你可以
画出几个符合条件的等腰三角形?并求符合
条件的等腰三角形的周长.
(3) 以长为3cm、5cm、7cm、10cm的四条线段中的
三条线段为边,可构成_____个三角形.摘苹果(1)任何三条线段都能组成一个三角形 ( ) (2)因为a+b>c,所以a、b、c三边可以构成三角形( )(4)已知等腰三角形的两边长分别为8cm,3cm,
则这三角形的周长为 ( ) (A) 14cm (B)19cm
(C) 14cm或19cm (D) 不确定 ××2B
智力大冲浪用3根长度相等的火柴棒可以搭成一个等边三角形(如图1),用5根长度相等的火柴棒可以搭成一个等腰三角形(如图2),用12根长度相等的火柴棒可以搭成几个三角形?它们分别是什么三角形?等腰三角形等边三角形直角三角形我学会了 3、三角形的稳定性1、三角形的三边关系定理;(2)确定三角形第三边的取值范围:
两边之差<第三边,
两边之和>第三边.课后作业:1、作业本2、能力超越题(我要试试,加油!)(1)已知三角形三边长为整数2,x-3,4,则共
可作出不同形状的三角形?当x为多少时,所
作三角形周长最长?(2) 已知三条线段a,b,c,满足下列关系式:
c=2a,b+2a =3c.这三条线段的长能组
成三角形吗?若能,请说明理由;若不能,请
举一个例子说明.
(3) 用16根等长的火柴棒摆成的三角形中,最长边
最多可以由____根火柴棒组成巩固练习
课本52页练习1、2、3。五. 小结这节课我们重点给大家介绍:1.三角形的任何两边的和大于第三边。2.已知三角形两边的长度,第三边长度范围是:大于这两边的差,小于这两边的和。3.三角形的稳定性六. 作业:
课本52页,习题8.2第
2、3 题。再见
道草坪一.实验 准备好长度分别为:2cm,3cm,5cm,6cm的牙签
各一根,从中任取三根看都能不能摆成一个三角形?从4根中取出3根有以下几种情况:(1)2cm,3cm,5cm通过动手发现: (3) (4) 可以摆成三角形,
(1) (2) 不能摆成三角形。通过实验你能发现
构成一个三角形的三边有什么规律?发现:三角形的任何两边的和大于第三边。(2)2cm,3cm,6cm(3)2cm,5cm,6cm(4)3cm,5cm,6cm二.画一个三边分别为7cm,5cm,4cm的三角形。画法步骤:(1)先画线段AB=7cm;(2)以点A为圆心,5cm长为半径画圆弧:(3)以点B为圆心,4cm长为半径画圆弧,
两弧相交于点C;(4)连接AC、BC 。试一试:你能用类似的方法画出三边长分别为:
9cm,4cm,4cm的三角形吗?例一. 有两根长度分别为5cm和8cm的木棒,现在再取
一根木棒与它们摆成一个三角形,你说第三根要多长呢?用长度为3cm的木棒行吗?为什么?用长度为14cm的木棒呢?已知三角形两边的长度,第三边长度范围是:如果告诉你:
三角形两边的长度,
第三边长度的范围你能确定吗?大于这两边的差,小于这两边的和。三. 三角形的稳定性1.三角形的三边确定了三角形的
形状和大小就完全确定了;
这个性质叫做三角形的稳定性。2.四边形有这个性质吗?3.你能举出三角形的稳定性在生产、
生活中应用的例子吗?只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形.下列长度的各组线段能否组成一个三角形?
(1)15cm、10cm、7cm (2) 4cm、5cm、10cm
(3) 3cm、8cm、5cm (4) 4cm、5cm、6cm练一练只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形.下列长度的各组线段能否组成一个三角形?
(1)15cm、10cm、7cm (2) 4cm、5cm、10cm
(3) 3cm、8cm、5cm (4) 4cm、5cm、6cm (2) 因为4cm+5cm<10cm,
所以这三条线段不能组成一个三角形. (3) 因为3cm+5cm=8cm,
所以这三条线段不能组成一个三角形.练一练 (4) 因为4cm+5cm>6cm,
所以这三条线段能组成一个三角形.1、已知两条线段的长分别是3cm、5cm ,
要想拼成一个三角形,问第三条线段a应
取的范围是多少? 试一试: 2、已知两条线段的长分别是3cm、5cm ,
要想拼成一个三角形,且第三条线段a的
长为奇数,问第三条线段应取多少长? 2cm
画出几个符合条件的等腰三角形?并求符合
条件的等腰三角形的周长.
(3) 以长为3cm、5cm、7cm、10cm的四条线段中的
三条线段为边,可构成_____个三角形.摘苹果(1)任何三条线段都能组成一个三角形 ( ) (2)因为a+b>c,所以a、b、c三边可以构成三角形( )(4)已知等腰三角形的两边长分别为8cm,3cm,
则这三角形的周长为 ( ) (A) 14cm (B)19cm
(C) 14cm或19cm (D) 不确定 ××2B
智力大冲浪用3根长度相等的火柴棒可以搭成一个等边三角形(如图1),用5根长度相等的火柴棒可以搭成一个等腰三角形(如图2),用12根长度相等的火柴棒可以搭成几个三角形?它们分别是什么三角形?等腰三角形等边三角形直角三角形我学会了 3、三角形的稳定性1、三角形的三边关系定理;(2)确定三角形第三边的取值范围:
两边之差<第三边,
两边之和>第三边.课后作业:1、作业本2、能力超越题(我要试试,加油!)(1)已知三角形三边长为整数2,x-3,4,则共
可作出不同形状的三角形?当x为多少时,所
作三角形周长最长?(2) 已知三条线段a,b,c,满足下列关系式:
c=2a,b+2a =3c.这三条线段的长能组
成三角形吗?若能,请说明理由;若不能,请
举一个例子说明.
(3) 用16根等长的火柴棒摆成的三角形中,最长边
最多可以由____根火柴棒组成巩固练习
课本52页练习1、2、3。五. 小结这节课我们重点给大家介绍:1.三角形的任何两边的和大于第三边。2.已知三角形两边的长度,第三边长度范围是:大于这两边的差,小于这两边的和。3.三角形的稳定性六. 作业:
课本52页,习题8.2第
2、3 题。再见
