9.1.4三角形的三边关系[下学期]
文档属性
| 名称 | 9.1.4三角形的三边关系[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 358.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-05-23 14:40:00 | ||
图片预览




文档简介
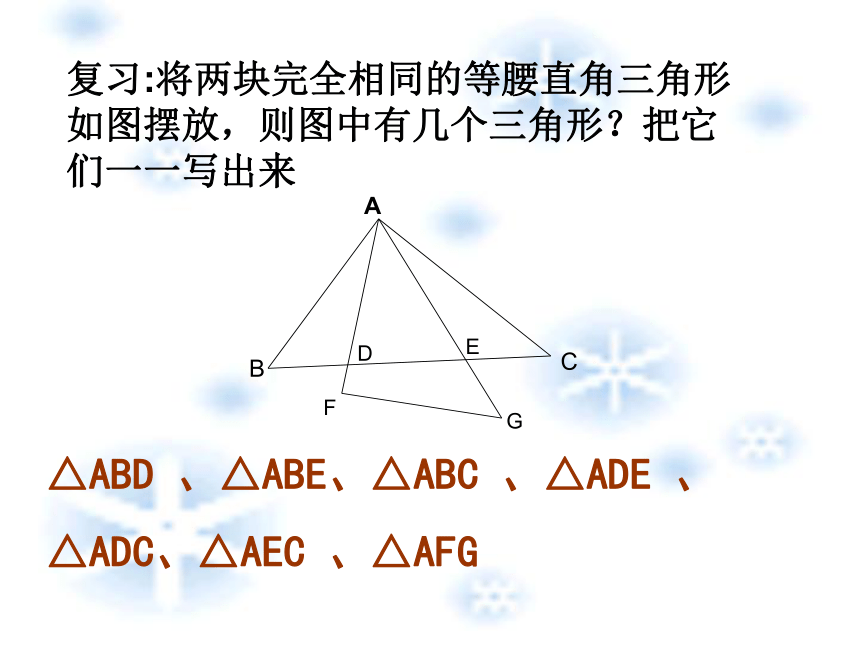
课件26张PPT。三角形三条边的关系复习:将两块完全相同的等腰直角三角形如图摆放,则图中有几个三角形?把它们一一写出来△ABD 、△ABE、△ABC 、△ADE 、
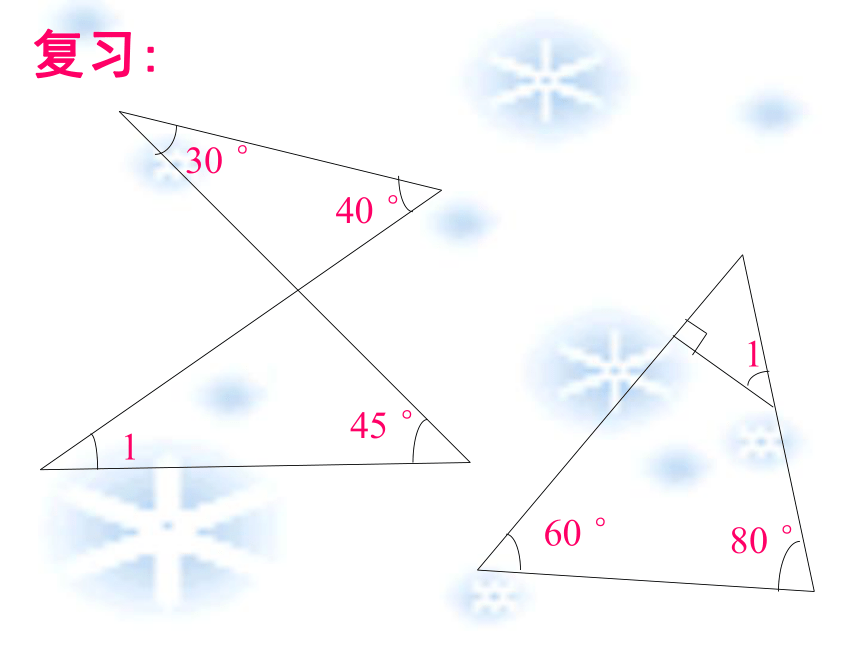
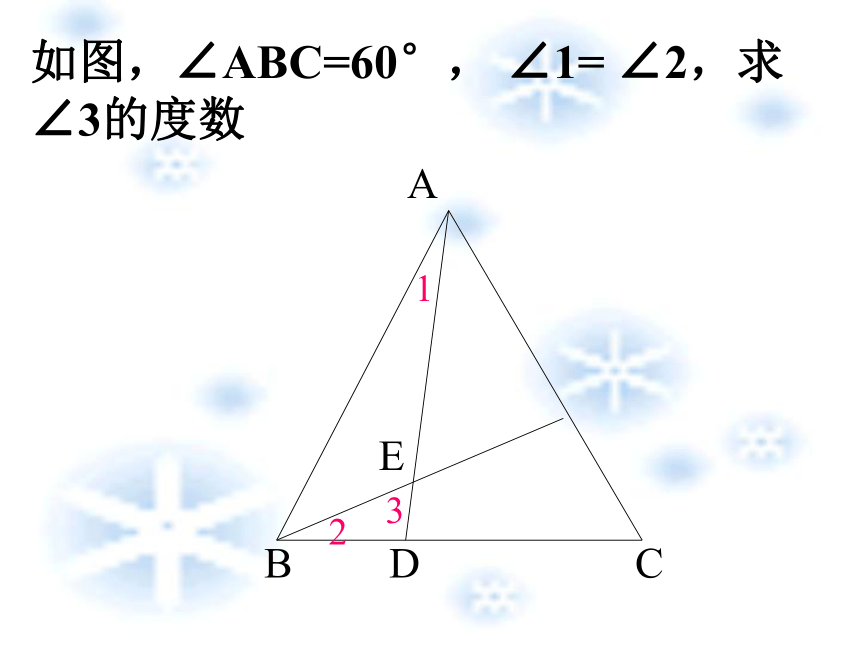
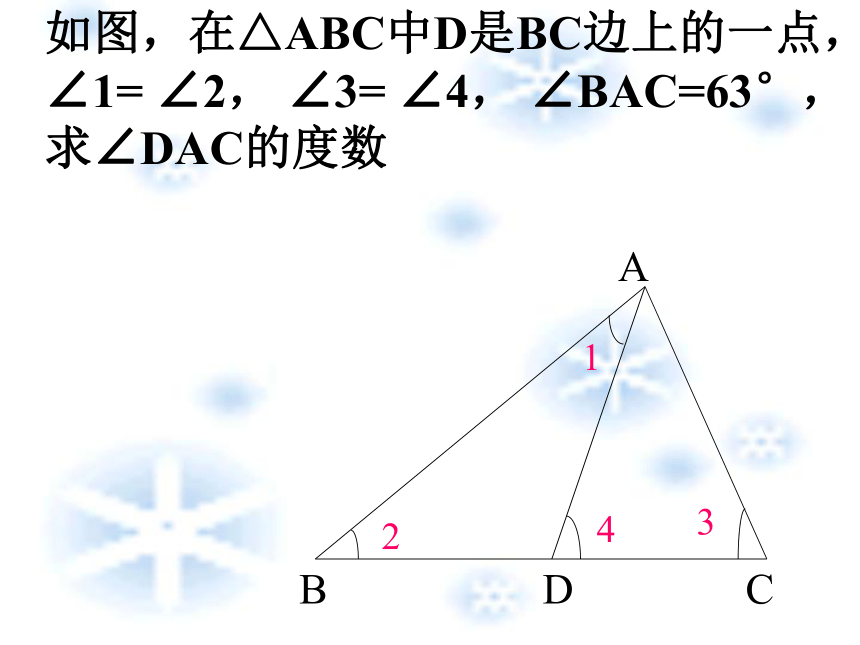
△ADC、△AEC 、△AFG 复习:如图,∠ABC=60°, ∠1= ∠2,求∠3的度数如图,在△ABC中D是BC边上的一点,∠1= ∠2, ∠3= ∠4, ∠BAC=63°,求∠DAC的度数探究: 如图三角形中,假设有一只小虫要从点B出
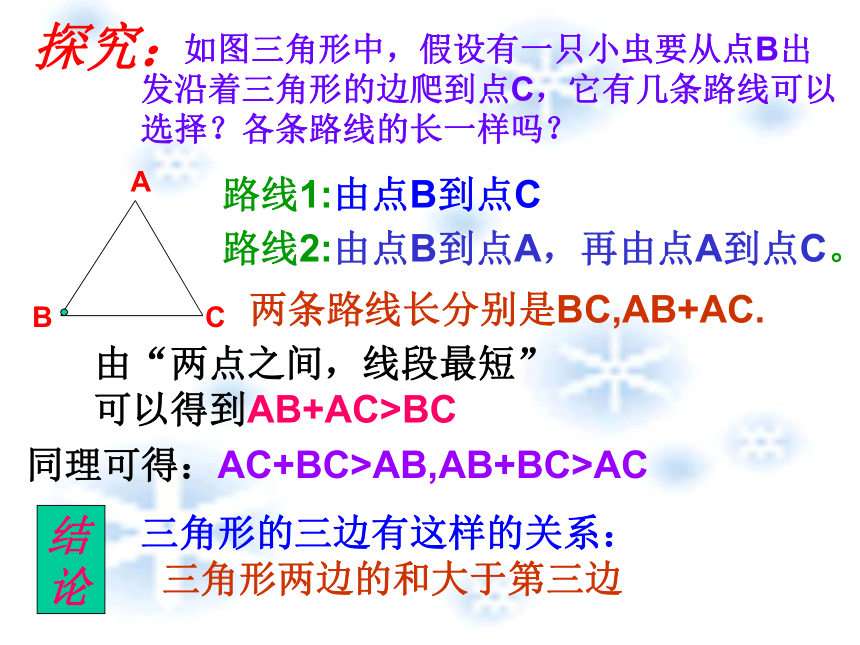
发沿着三角形的边爬到点C,它有几条路线可以
选择?各条路线的长一样吗?路线1:由点B到点C路线2:由点B到点A,再由点A到点C。两条路线长分别是BC,AB+AC.由“两点之间,线段最短”
可以得到AB+AC>BC同理可得:AC+BC>AB,AB+BC>AC三角形的三边有这样的关系:
三角形两边的和大于第三边结论试一试下列长度的三条线段能否组成三角形?为什么?(1)3 , 4, 8 (2)5 , 6 , 11 (3)5 , 6, 10解:(1)不能组成三角形,因为3+4<8,即两条线段的和
小于第三条线段,所以不能组成三角形;(2)不能组成三角形,因为5+6=11即两条线段的和
等于第三条直线,所以不能组成三角形;(3)能组成三角形,因为任意两条线段的和都大于
第三条线段。判断三条线段能否组成三角形,是否一定要检验
三条线段中任何两条的和都大于第三条?根据你
刚才解题经验,有没有更简便的判断方法? 思考练一练1.下列长度的三条线段能否组成三角形?为什么?(1) 3,4,8 ( )
(2) 2,5,6 ( )
(3) 5,6,10 ( )
(4) 3,5,8 ( ) 不能能能不能 2.小明有长为2cm,4cm,5cm,7cm的四根木条,任意选其中三根组成三角形,他能组成几个三角形? 3.一个等腰三角形的周长是36cm,已知其中一边长等于10,求其他两边长。若其中一边长等于8,则其他两边长为多少?试一试,能否画一个三角形,使它的三边分别为:(1)7cm,5cm,4cm(2)7cm,4cm,2cm(3)9cm,5cm,4cm得出结论:三角形的任何两边的和大于第三边你能否用以前学过的线段的基本性质来说明这一结论的正确性?两点之间,线段最短例1、(1)以下列数据为长度的四组线段中,能组成三角形的是A、4,10,6 B、4,11,6 C、10,5,5 D、6,4,9(2) 满足下列条件的三条线段 a、b、c中,不能构成三角形的是A、a=m+1 b=m+2 c=m+3 (m>0)
B、a:b:c=2:3:5
C、a=1/5 b=1/2 c=1/3
D、a=2k b=3k c=5k-1 (k≥1)例2、△ABC中,AB=2,BC=9,求第三边AC的 取值范围;例3、(1)等腰三角形的两边长为6和8,求其周长(2)等腰三角形的两边长为2和5,求其周长(3)等腰三角形的一边长为6,周长为14,求另两边长若第三边长为奇数,求三角形的周长1、等腰三角形的两边长分别为9cm和4cm,则它的周长是______cm2.已知三角形两边长分别为7和2。若它的周长是奇数,则第三边长是_____3. △ABC中,AB=7,BC=8,则AC的取值范围是_____4.两根木棒的长分别是5cm和7cm,要选择第三根,将它们钉成一个三角形,如果第三根木棒的长为偶数,那么第三根木棒长的取值情况是( )
A.3种 B.4种 C.5种 D.6种4.等腰三角形ABC中,一腰AC上的中线BM把三角形周长分为12cm和15cm两部分,求三角形ABC各边的长.二.三角形的稳定性生活的思考做一做三角形具有稳定性,
四边形具有不稳定性.结论:说一说在日常生活中三角形稳定性有什么应用?练一练1、下列图形中具有稳定性的是( ) (A)正方形 (B)长方形
(C)直角三角形 (D)平行四边形2、要使下列木架稳定各至少需要多少根木棍?C3、下列图中具有稳定性的有( )A 1个 B 2个 C 3个 D 4个C1、判断:已知a+b>c,则以线段a、b、c为边能构成三角形。( )2、在ΔABC中,AB=10,BC=2,并且AC为奇数,那么ΔABC的周长为 。3、如图,已知BM是ΔABC的中线,AB=6,BC=8,那么ΔMBC的周长与ΔABM的周长相差 。21或23?2综合应用: 4、如果一个三角形的三条高的交点恰好是这个三角形的顶点,那么这个三角形是( )(A)锐角三角形 (B)钝角三角形
(C)直角三角形 (D)难以确定C 5、长为10,7,5,3的四根木条,选其中三根组成三角形,有几种选法?为什么?6、如图,?ABC中,AB=2㎝,BC=4㎝。 ?ABC的高AD与CE的比是多少? 7、如图,AD是?ABC的角平分线。DE∥AC,DE交AB于E,DF∥AB,DF交AC于F。图中∠1与∠2有什么关系?为什么?
△ADC、△AEC 、△AFG 复习:如图,∠ABC=60°, ∠1= ∠2,求∠3的度数如图,在△ABC中D是BC边上的一点,∠1= ∠2, ∠3= ∠4, ∠BAC=63°,求∠DAC的度数探究: 如图三角形中,假设有一只小虫要从点B出
发沿着三角形的边爬到点C,它有几条路线可以
选择?各条路线的长一样吗?路线1:由点B到点C路线2:由点B到点A,再由点A到点C。两条路线长分别是BC,AB+AC.由“两点之间,线段最短”
可以得到AB+AC>BC同理可得:AC+BC>AB,AB+BC>AC三角形的三边有这样的关系:
三角形两边的和大于第三边结论试一试下列长度的三条线段能否组成三角形?为什么?(1)3 , 4, 8 (2)5 , 6 , 11 (3)5 , 6, 10解:(1)不能组成三角形,因为3+4<8,即两条线段的和
小于第三条线段,所以不能组成三角形;(2)不能组成三角形,因为5+6=11即两条线段的和
等于第三条直线,所以不能组成三角形;(3)能组成三角形,因为任意两条线段的和都大于
第三条线段。判断三条线段能否组成三角形,是否一定要检验
三条线段中任何两条的和都大于第三条?根据你
刚才解题经验,有没有更简便的判断方法? 思考练一练1.下列长度的三条线段能否组成三角形?为什么?(1) 3,4,8 ( )
(2) 2,5,6 ( )
(3) 5,6,10 ( )
(4) 3,5,8 ( ) 不能能能不能 2.小明有长为2cm,4cm,5cm,7cm的四根木条,任意选其中三根组成三角形,他能组成几个三角形? 3.一个等腰三角形的周长是36cm,已知其中一边长等于10,求其他两边长。若其中一边长等于8,则其他两边长为多少?试一试,能否画一个三角形,使它的三边分别为:(1)7cm,5cm,4cm(2)7cm,4cm,2cm(3)9cm,5cm,4cm得出结论:三角形的任何两边的和大于第三边你能否用以前学过的线段的基本性质来说明这一结论的正确性?两点之间,线段最短例1、(1)以下列数据为长度的四组线段中,能组成三角形的是A、4,10,6 B、4,11,6 C、10,5,5 D、6,4,9(2) 满足下列条件的三条线段 a、b、c中,不能构成三角形的是A、a=m+1 b=m+2 c=m+3 (m>0)
B、a:b:c=2:3:5
C、a=1/5 b=1/2 c=1/3
D、a=2k b=3k c=5k-1 (k≥1)例2、△ABC中,AB=2,BC=9,求第三边AC的 取值范围;例3、(1)等腰三角形的两边长为6和8,求其周长(2)等腰三角形的两边长为2和5,求其周长(3)等腰三角形的一边长为6,周长为14,求另两边长若第三边长为奇数,求三角形的周长1、等腰三角形的两边长分别为9cm和4cm,则它的周长是______cm2.已知三角形两边长分别为7和2。若它的周长是奇数,则第三边长是_____3. △ABC中,AB=7,BC=8,则AC的取值范围是_____4.两根木棒的长分别是5cm和7cm,要选择第三根,将它们钉成一个三角形,如果第三根木棒的长为偶数,那么第三根木棒长的取值情况是( )
A.3种 B.4种 C.5种 D.6种4.等腰三角形ABC中,一腰AC上的中线BM把三角形周长分为12cm和15cm两部分,求三角形ABC各边的长.二.三角形的稳定性生活的思考做一做三角形具有稳定性,
四边形具有不稳定性.结论:说一说在日常生活中三角形稳定性有什么应用?练一练1、下列图形中具有稳定性的是( ) (A)正方形 (B)长方形
(C)直角三角形 (D)平行四边形2、要使下列木架稳定各至少需要多少根木棍?C3、下列图中具有稳定性的有( )A 1个 B 2个 C 3个 D 4个C1、判断:已知a+b>c,则以线段a、b、c为边能构成三角形。( )2、在ΔABC中,AB=10,BC=2,并且AC为奇数,那么ΔABC的周长为 。3、如图,已知BM是ΔABC的中线,AB=6,BC=8,那么ΔMBC的周长与ΔABM的周长相差 。21或23?2综合应用: 4、如果一个三角形的三条高的交点恰好是这个三角形的顶点,那么这个三角形是( )(A)锐角三角形 (B)钝角三角形
(C)直角三角形 (D)难以确定C 5、长为10,7,5,3的四根木条,选其中三根组成三角形,有几种选法?为什么?6、如图,?ABC中,AB=2㎝,BC=4㎝。 ?ABC的高AD与CE的比是多少? 7、如图,AD是?ABC的角平分线。DE∥AC,DE交AB于E,DF∥AB,DF交AC于F。图中∠1与∠2有什么关系?为什么?
