三角形的外角和[上学期]
图片预览



文档简介
课件8张PPT。知识连接:
三角形的内角和等于180°;
邻补角;
外角 。2. 三角形的外角和学习目标:
掌握两种分析三角形外角和的方法;
根据三角形的内外角和, 求三角形的内外角;知识回顾:三角形中内角的一边与另一边的反向延长线所组成的角叫做三角形的外角 显然有
?∠CBD(外角)+∠ABC(相邻内角)=180°
∠A+∠C +∠ABC =180° (内角和公式)
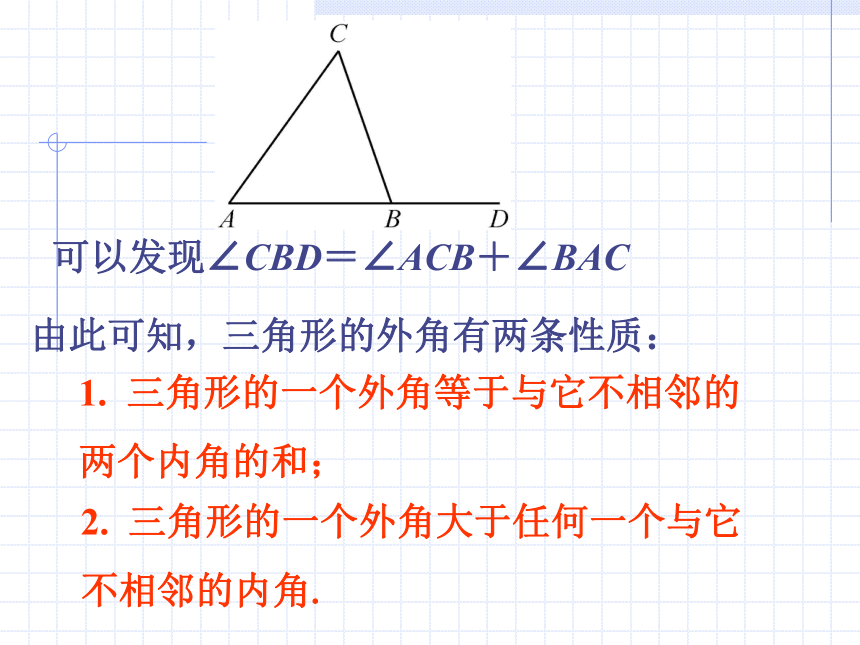
外角和可以发现∠CBD=∠ACB+∠BAC由此可知,三角形的外角有两条性质:2.? 三角形的一个外角大于任何一个与它
不相邻的内角.1.??三角形的一个外角等于与它不相邻的
两个内角的和;例1??如图8.2.9,D是△ABC的BC边上一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.求:(1)∠B的度数;(2)∠C的度数.
解 (1)因为∠ADC是△ABD的外角,
所以∠ADC=∠B+∠BAD=80°.
又 ∠B=∠BAD,
所以∠B=80°×0.5=40°.
(2)在△ABC中,
因为∠B+∠BAC+∠C=180°,
所以∠C=180°-∠B-∠BAC
=180°-40°-70°
=70°三角形的外角和等于360°. ∠1+______________=180°,
∠2+_______________=180°,
∠3+_______________=180°.
三式相加可以得到
∠1+∠2+∠3+______+______+______=_______, ∠ACB
∠BAC
∠ABC
∠ACB ∠BAC ∠ABC 540 °3∠1+∠2+∠3 =_________? 练 习
1.(口答)一个三角形可以有两个内角都是直角吗?可以有两个内角都是钝角或都是锐角吗?为什么?
2.已知∠A、∠B、∠C是△ABC的三个内角.
(1如果∠A=90°,∠C=55°,那么∠B=______;
(2 如果∠A=90°,∠B-∠C=24°,那么∠B=_____,∠C=______;
(3如果∠C=4∠A,∠A+∠B=100°,那么∠A=______,∠B=______,与∠C相邻的外角=_______.
.
35 °57 °33°20°80 °100° 3.求下列各图中∠1的度数
4.如图,在直角△ABC中,CD是斜
边AB上的高,∠BCD=35°,求
∠A与∠EBC的度数.
小结:三角形的外角性质:
三角形的一个外角等于与它不相邻的两个内角的和;
三角形的一个外角大于任何一个与它不相邻的内角.
三角形的内、外角和:
三角形的内角和为180°;
三角形的外角和为360°;
三角形的内角和等于180°;
邻补角;
外角 。2. 三角形的外角和学习目标:
掌握两种分析三角形外角和的方法;
根据三角形的内外角和, 求三角形的内外角;知识回顾:三角形中内角的一边与另一边的反向延长线所组成的角叫做三角形的外角 显然有
?∠CBD(外角)+∠ABC(相邻内角)=180°
∠A+∠C +∠ABC =180° (内角和公式)
外角和可以发现∠CBD=∠ACB+∠BAC由此可知,三角形的外角有两条性质:2.? 三角形的一个外角大于任何一个与它
不相邻的内角.1.??三角形的一个外角等于与它不相邻的
两个内角的和;例1??如图8.2.9,D是△ABC的BC边上一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.求:(1)∠B的度数;(2)∠C的度数.
解 (1)因为∠ADC是△ABD的外角,
所以∠ADC=∠B+∠BAD=80°.
又 ∠B=∠BAD,
所以∠B=80°×0.5=40°.
(2)在△ABC中,
因为∠B+∠BAC+∠C=180°,
所以∠C=180°-∠B-∠BAC
=180°-40°-70°
=70°三角形的外角和等于360°. ∠1+______________=180°,
∠2+_______________=180°,
∠3+_______________=180°.
三式相加可以得到
∠1+∠2+∠3+______+______+______=_______, ∠ACB
∠BAC
∠ABC
∠ACB ∠BAC ∠ABC 540 °3∠1+∠2+∠3 =_________? 练 习
1.(口答)一个三角形可以有两个内角都是直角吗?可以有两个内角都是钝角或都是锐角吗?为什么?
2.已知∠A、∠B、∠C是△ABC的三个内角.
(1如果∠A=90°,∠C=55°,那么∠B=______;
(2 如果∠A=90°,∠B-∠C=24°,那么∠B=_____,∠C=______;
(3如果∠C=4∠A,∠A+∠B=100°,那么∠A=______,∠B=______,与∠C相邻的外角=_______.
.
35 °57 °33°20°80 °100° 3.求下列各图中∠1的度数
4.如图,在直角△ABC中,CD是斜
边AB上的高,∠BCD=35°,求
∠A与∠EBC的度数.
小结:三角形的外角性质:
三角形的一个外角等于与它不相邻的两个内角的和;
三角形的一个外角大于任何一个与它不相邻的内角.
三角形的内、外角和:
三角形的内角和为180°;
三角形的外角和为360°;
