湘教版数学八年级下册3.1 第1课时 平面直角坐标系课时习题(含答案)
文档属性
| 名称 | 湘教版数学八年级下册3.1 第1课时 平面直角坐标系课时习题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 631.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-05 00:00:00 | ||
图片预览


文档简介
3.1 平面直角坐标系
第1课时 平面直角坐标系
要点感知1 在平面内互相__________且有公共原点的__________数轴组成平面直角坐标系.
预习练习1-1 在平面直角坐标系中,原点的坐标为__________.
要点感知2 平面上的点与有序实数对__________对应.
预习练习2-1 下列关于有序数对的说法正确的是( )
A.(3,2)与(2,3)表示的位置相同
B.(a,b)与(b,a)表示的位置一定不同
C.(3,-2)与(-2,3)是表示不同位置的两个有序数对
D.(4,4)与(4,4)可以表示两个不同的位置
要点感知3 在平面内点的坐标特征:
预习练习3-1 在平面直角坐标系中,点A(2,-3)在第__________象限( )
A.一 B.二 C.三 D.四
知识点1 平面直角坐标系中由点写出坐标
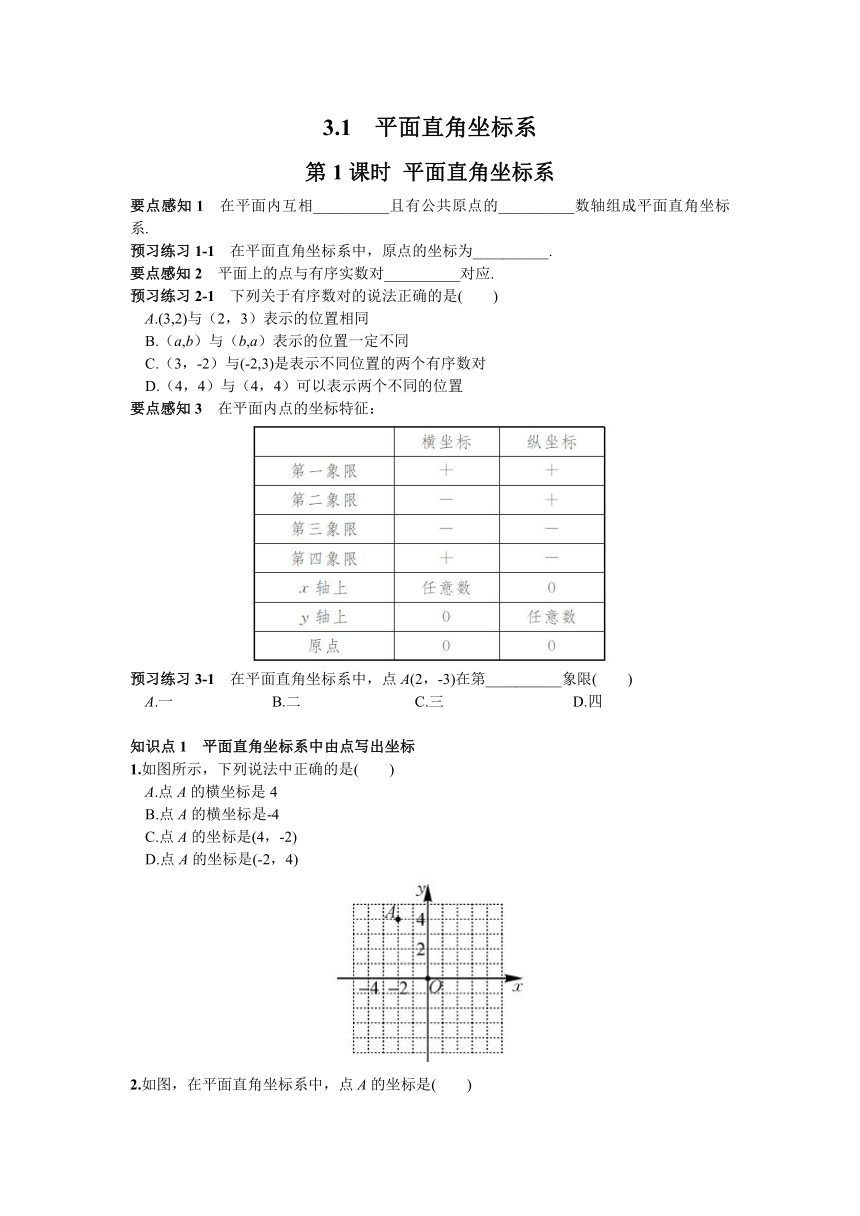
1.如图所示,下列说法中正确的是( )
A.点A的横坐标是4
B.点A的横坐标是-4
C.点A的坐标是(4,-2)
D.点A的坐标是(-2,4)
2.如图,在平面直角坐标系中,点A的坐标是( )
A.(-2,-3) B.(3,-2) C.(2,3) D.(-2,3)
知识点2 平面直角坐标系中由坐标描点
3.在平面直角坐标系中,依次描出下列各点,并将各组内的点依次连接起来:
(1)(2,1),(2,0),(3,0),(3,4);
(2)(3,6),(0,4),(6,4),(3,6).
你发现所得的图形是( )
A.两个三角形 B.房子 C.雨伞 D.电灯
4.建立适当的平面直角坐标系,并在图中描出坐标是A(2,3),B(-2,3),C(3,-2),D(5,1),E(0,-4),F(-3,0)的各点.
知识点3 点的坐标的符号特征
5.如图,小明用手盖住的点的坐标可能为( )
A.(2,3) B.(2,-3) C.(-2,3) D.(-2,-3)
6.在平面直角坐标系中,点P的坐标为(-2,a2+1),则点P所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.在平面直角坐标系中,若点P(a,b)在第二象限,则点Q(1-a,-b)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.平面直角坐标系中,在第二象限内有一点P,且P点到x轴的距离是4,到y轴的距离是5,则P点坐标为( )
A.(-5,4) B.(-4,5) C.(4,5) D.(5,-4)
9.若点P(a,a-2)在第四象限,则a的取值范围是( )
A.-2<a<0 B.0<a<2 C.a>2 D.a<0
10.若点M(x,y)满足(x+y)2=x2+y2-2,则点M所在象限是( )
A.第一象限或第三象限
B.第二象限或第四象限
C.第一象限或第二象限
D.不能确定
11.如果m是任意实数,那么点P(m-4,m+1)一定不在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
12.若点M(a+3,a-2)在x轴上,则a=__________.
13.在平面直角坐标系中,若点M(1,3)与点N(x,3)之间的距离是5,则x的值是__________.
14.如图,在平面直角坐标系xOy中,已知点A(3,4),将OA绕坐标原点O逆时针旋转90°到OA′,则点A′的坐标是__________.
15.在平面直角坐标系内,已知点A(1-2k,k-2)在第三象限,且k为整数,求k的值.
16.如果点P(3m-2,3-m)到x轴的距离与它到y轴的距离相等,求m的值.
17.在平面直角坐标系中,孔明做走棋的游戏,其走法是:棋子从原点出发,第1步向右走1个单位,第2步向右走2个单位,第3步向上走1个单位,第4步向右走1个单位…,依此类推,第n步的走法是:当n能被3整除时,则向上走1个单位;当n被3除,余数为1时,则向右走1个单位;当n被3除,余数为2时,则向右走2个单位(温馨提示:根据走法,每3步为一个循环组依次循环).当走完第100步时,棋子所处位置的坐标是( )
A.(66,34) B.(67,33) C.(100,33) D.(99,34)
18.一个质点在第一象限及x轴、y轴上运动,在第一秒钟,它从原点运动到(0,1),然后接着按图中箭头所示方向运动{即(0,0)-(0,1)-(1,1)-(1,0)…},且每秒移动一个单位,求第35秒时质点所在位置的坐标.
参考答案
要点感知1 垂直 两条
预习练习1-1 (0,0)
要点感知2 一一
预习练习2-1 C
预习练习3-1 D
1.D 2.D 3.C
4.如图所示.
5.B 6.B 7.D
8.A 9.B 10.B 11.D 12.2 13.-4或6 14.(-4,3)
15.∵点A(1-2k,k-2)在第三象限,
∴解得0.5<k<2.
又∵k为整数,
∴k=1.
16.由题意知:|3m-2|=|3-m|.
∴3m-2=±(3-m).
当3m-2=+(3-m)时,m=;
当3m-2=-(3-m)时,m=-.
∴m=或-.
17.C
18.由题意可知质点移动的速度是1个单位长度/秒,到达(1,0)时用了3秒,到达(2,0)时用了4秒;
从(2,0)到(0,2)有四个单位长度,则到达(0,2)时用了4+4=8秒,到(0,3)时用了9秒;
从(0,3)到(3,0)有六个单位长度,则到(3,0)时用9+6=15秒;
依次类推到(4,0)用16秒,到(0,4)用16+8=24秒,到(0,5)用25秒,到(5,0)用25+10=35秒.
故第35秒时质点到达的位置坐标为(5,0).
第1课时 平面直角坐标系
要点感知1 在平面内互相__________且有公共原点的__________数轴组成平面直角坐标系.
预习练习1-1 在平面直角坐标系中,原点的坐标为__________.
要点感知2 平面上的点与有序实数对__________对应.
预习练习2-1 下列关于有序数对的说法正确的是( )
A.(3,2)与(2,3)表示的位置相同
B.(a,b)与(b,a)表示的位置一定不同
C.(3,-2)与(-2,3)是表示不同位置的两个有序数对
D.(4,4)与(4,4)可以表示两个不同的位置
要点感知3 在平面内点的坐标特征:
预习练习3-1 在平面直角坐标系中,点A(2,-3)在第__________象限( )
A.一 B.二 C.三 D.四
知识点1 平面直角坐标系中由点写出坐标
1.如图所示,下列说法中正确的是( )
A.点A的横坐标是4
B.点A的横坐标是-4
C.点A的坐标是(4,-2)
D.点A的坐标是(-2,4)
2.如图,在平面直角坐标系中,点A的坐标是( )
A.(-2,-3) B.(3,-2) C.(2,3) D.(-2,3)
知识点2 平面直角坐标系中由坐标描点
3.在平面直角坐标系中,依次描出下列各点,并将各组内的点依次连接起来:
(1)(2,1),(2,0),(3,0),(3,4);
(2)(3,6),(0,4),(6,4),(3,6).
你发现所得的图形是( )
A.两个三角形 B.房子 C.雨伞 D.电灯
4.建立适当的平面直角坐标系,并在图中描出坐标是A(2,3),B(-2,3),C(3,-2),D(5,1),E(0,-4),F(-3,0)的各点.
知识点3 点的坐标的符号特征
5.如图,小明用手盖住的点的坐标可能为( )
A.(2,3) B.(2,-3) C.(-2,3) D.(-2,-3)
6.在平面直角坐标系中,点P的坐标为(-2,a2+1),则点P所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.在平面直角坐标系中,若点P(a,b)在第二象限,则点Q(1-a,-b)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.平面直角坐标系中,在第二象限内有一点P,且P点到x轴的距离是4,到y轴的距离是5,则P点坐标为( )
A.(-5,4) B.(-4,5) C.(4,5) D.(5,-4)
9.若点P(a,a-2)在第四象限,则a的取值范围是( )
A.-2<a<0 B.0<a<2 C.a>2 D.a<0
10.若点M(x,y)满足(x+y)2=x2+y2-2,则点M所在象限是( )
A.第一象限或第三象限
B.第二象限或第四象限
C.第一象限或第二象限
D.不能确定
11.如果m是任意实数,那么点P(m-4,m+1)一定不在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
12.若点M(a+3,a-2)在x轴上,则a=__________.
13.在平面直角坐标系中,若点M(1,3)与点N(x,3)之间的距离是5,则x的值是__________.
14.如图,在平面直角坐标系xOy中,已知点A(3,4),将OA绕坐标原点O逆时针旋转90°到OA′,则点A′的坐标是__________.
15.在平面直角坐标系内,已知点A(1-2k,k-2)在第三象限,且k为整数,求k的值.
16.如果点P(3m-2,3-m)到x轴的距离与它到y轴的距离相等,求m的值.
17.在平面直角坐标系中,孔明做走棋的游戏,其走法是:棋子从原点出发,第1步向右走1个单位,第2步向右走2个单位,第3步向上走1个单位,第4步向右走1个单位…,依此类推,第n步的走法是:当n能被3整除时,则向上走1个单位;当n被3除,余数为1时,则向右走1个单位;当n被3除,余数为2时,则向右走2个单位(温馨提示:根据走法,每3步为一个循环组依次循环).当走完第100步时,棋子所处位置的坐标是( )
A.(66,34) B.(67,33) C.(100,33) D.(99,34)
18.一个质点在第一象限及x轴、y轴上运动,在第一秒钟,它从原点运动到(0,1),然后接着按图中箭头所示方向运动{即(0,0)-(0,1)-(1,1)-(1,0)…},且每秒移动一个单位,求第35秒时质点所在位置的坐标.
参考答案
要点感知1 垂直 两条
预习练习1-1 (0,0)
要点感知2 一一
预习练习2-1 C
预习练习3-1 D
1.D 2.D 3.C
4.如图所示.
5.B 6.B 7.D
8.A 9.B 10.B 11.D 12.2 13.-4或6 14.(-4,3)
15.∵点A(1-2k,k-2)在第三象限,
∴解得0.5<k<2.
又∵k为整数,
∴k=1.
16.由题意知:|3m-2|=|3-m|.
∴3m-2=±(3-m).
当3m-2=+(3-m)时,m=;
当3m-2=-(3-m)时,m=-.
∴m=或-.
17.C
18.由题意可知质点移动的速度是1个单位长度/秒,到达(1,0)时用了3秒,到达(2,0)时用了4秒;
从(2,0)到(0,2)有四个单位长度,则到达(0,2)时用了4+4=8秒,到(0,3)时用了9秒;
从(0,3)到(3,0)有六个单位长度,则到(3,0)时用9+6=15秒;
依次类推到(4,0)用16秒,到(0,4)用16+8=24秒,到(0,5)用25秒,到(5,0)用25+10=35秒.
故第35秒时质点到达的位置坐标为(5,0).
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
