物理人教版(2019)必修第二册7.1行星的运动(共24张ppt)
文档属性
| 名称 | 物理人教版(2019)必修第二册7.1行星的运动(共24张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 25.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-05-05 15:51:35 | ||
图片预览







文档简介
(共24张PPT)
第一节 行星的运动
第七章 万有引力与宇宙航行
人教版高中物理(2019)必修第二册
人们为什么要研究天文?
你知道哪些古代的宇宙结构学说?
盖天说
浑天说
宣夜说
古希腊亚里士多德的“天球”学说
地心说
“荧惑守心”
托勒密(90-168),代表作《天文学大成》
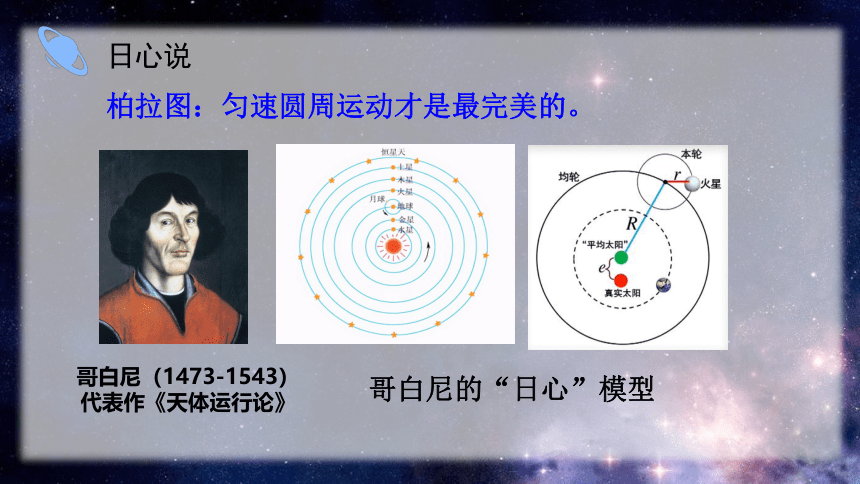
日心说
柏拉图:匀速圆周运动才是最完美的。
哥白尼(1473-1543)
代表作《天体运行论》
哥白尼的“日心”模型
“天空立法者”开普勒
德国天文学家、数学家和占星家
1571年,生于德国
1589年,就读于图宾根大学
1596年,著《宇宙的奥秘》
1609年,著《新天文学》
1619年,著《世界的和谐》
1627年,整理《鲁道夫天文表》
1630年,逝于雷根斯堡
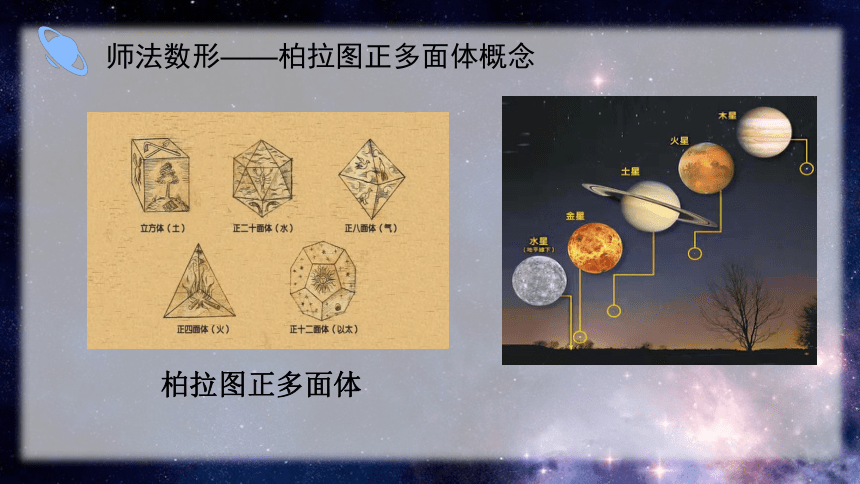
师法数形——柏拉图正多面体概念
柏拉图正多面体
师法数形——数的和谐和美学理念
毕达哥拉斯
数的比例和音程之美
行星半径、运行速率的差异
演奏出“天体的音乐”
天体运动不是别的,不过是几种声音汇成一种连续的音乐。
这种音乐只能为心智所领悟,不能被人的耳朵倾听。
——开普勒
开普勒的“五体”宇宙
规则、对称之美——与当时行星轨道数据近似匹配
星学之王第谷
第谷(1546-1601)
“前望远镜时代”天文观测最高精度
第谷与开普勒
第谷
开普勒
美妙的数学逻辑(寻理)
精准的观测数据(唯实)
第谷掌握了最好的观察资料,这就如他掌握了建设一座大厦的物质基础一样。他可以说富甲天下,但就像天下大多数富人那样,他不知道如何恰当使用这些财富。 ——开普勒
开普勒的思想基础
第谷20余年的观测记录达到当时的精度巅峰
坚信第谷数据的准确性
支持哥白尼日心说的观点
日心说时太阳系行星轨道生成圆由80减到34
秉承数的和谐的美学理念
毕达哥拉斯学派数的美学观、匀速圆周运动的和谐
开普勒的归纳推演
从火星轨道的研究入手
用日心坐标系替换地心坐标系
用圆形轨道计算火星理论上的运动
结果与第谷的观测数据仍有8’误差!
转换思维:抛弃传统美学观
确立了利用数学逻辑和数字关系研究天体运动规律的思路
开普勒第一定律
所有的行星围绕太阳运动的轨道都是椭圆,太阳处在所有椭圆的一个焦点上。
说明:
地球的公转轨道不是圆而是椭圆
太阳并不是位于椭圆中心,而是位于焦点处。
开普勒第一定律也常说成轨道定律
开普勒第二定律
对于任意一个行星而言,它和太阳的连线在相等的时间内扫过相等的面积。
开普勒第二定律也常说成面积定律
说明:
行星在近日点速率大于远日点速率。
“均匀性”的别样体现
开普勒第二定律
春夏两季(186天)比
秋冬两季(179天)要长。
你认为春夏两季的时间长还是秋冬两季的时间长?
开普勒第三定律
行星公转周期T与公转轨道半长轴a的关系?
水星 金星 地球 火星 木星 土星
周期(天) 87.97 225 365 687 4333 10759
半长轴(×106km) 57 108 149 228 778 1426
以你所学的数学知识,怎么更快地发现T与a的关系?
水星 金星 地球 火星 木星 土星
T2(年) 7738 50625 133225 471969 18774889 115756081
a3(×106km) 185193 1.26×106 3.3×106 1.18×107 4.71×108 2.90×109
a3/T2 3.36×1018 3.36×1018 3.36×1018 3.36×1018 3.36×1018 3.36×1018
开普勒第三定律
所有行星轨道的半长轴的三次方跟它的公转周期的二次方的比都相等。
开普勒第三定律也常说成周期定律
开普勒第三定律
k值与中心天体有关
中心天体既可以是恒星
也可以是行星
行星/卫星 半长轴(106km) 周期(天) k(m /s )
水星 57 87.97
金星 108 225
地球 149 365
火星 228 687
木星 778 4333
土星 1426 10759
天王星 2870 30660
海王星 4498 60148
月球 0.3844 27.3
同步卫星 0.0424 1
3.36×1018
3.36×1018
3.36×1018
3.36×1018
3.36×1018
3.36×1018
3.37×1018
3.37×1018
1.03×1013
1.03×1013
开普勒三定律
行星公转轨道可近似看做圆轨道
开普勒三定律
行星公转可近似看做匀速圆周运动
开普勒三定律
开普勒第三定律
转化为:
椭圆半长轴a
转变为圆的半径r
课堂小结
宇宙有没有中心?
第一节 行星的运动
第七章 万有引力与宇宙航行
人教版高中物理(2019)必修第二册
人们为什么要研究天文?
你知道哪些古代的宇宙结构学说?
盖天说
浑天说
宣夜说
古希腊亚里士多德的“天球”学说
地心说
“荧惑守心”
托勒密(90-168),代表作《天文学大成》
日心说
柏拉图:匀速圆周运动才是最完美的。
哥白尼(1473-1543)
代表作《天体运行论》
哥白尼的“日心”模型
“天空立法者”开普勒
德国天文学家、数学家和占星家
1571年,生于德国
1589年,就读于图宾根大学
1596年,著《宇宙的奥秘》
1609年,著《新天文学》
1619年,著《世界的和谐》
1627年,整理《鲁道夫天文表》
1630年,逝于雷根斯堡
师法数形——柏拉图正多面体概念
柏拉图正多面体
师法数形——数的和谐和美学理念
毕达哥拉斯
数的比例和音程之美
行星半径、运行速率的差异
演奏出“天体的音乐”
天体运动不是别的,不过是几种声音汇成一种连续的音乐。
这种音乐只能为心智所领悟,不能被人的耳朵倾听。
——开普勒
开普勒的“五体”宇宙
规则、对称之美——与当时行星轨道数据近似匹配
星学之王第谷
第谷(1546-1601)
“前望远镜时代”天文观测最高精度
第谷与开普勒
第谷
开普勒
美妙的数学逻辑(寻理)
精准的观测数据(唯实)
第谷掌握了最好的观察资料,这就如他掌握了建设一座大厦的物质基础一样。他可以说富甲天下,但就像天下大多数富人那样,他不知道如何恰当使用这些财富。 ——开普勒
开普勒的思想基础
第谷20余年的观测记录达到当时的精度巅峰
坚信第谷数据的准确性
支持哥白尼日心说的观点
日心说时太阳系行星轨道生成圆由80减到34
秉承数的和谐的美学理念
毕达哥拉斯学派数的美学观、匀速圆周运动的和谐
开普勒的归纳推演
从火星轨道的研究入手
用日心坐标系替换地心坐标系
用圆形轨道计算火星理论上的运动
结果与第谷的观测数据仍有8’误差!
转换思维:抛弃传统美学观
确立了利用数学逻辑和数字关系研究天体运动规律的思路
开普勒第一定律
所有的行星围绕太阳运动的轨道都是椭圆,太阳处在所有椭圆的一个焦点上。
说明:
地球的公转轨道不是圆而是椭圆
太阳并不是位于椭圆中心,而是位于焦点处。
开普勒第一定律也常说成轨道定律
开普勒第二定律
对于任意一个行星而言,它和太阳的连线在相等的时间内扫过相等的面积。
开普勒第二定律也常说成面积定律
说明:
行星在近日点速率大于远日点速率。
“均匀性”的别样体现
开普勒第二定律
春夏两季(186天)比
秋冬两季(179天)要长。
你认为春夏两季的时间长还是秋冬两季的时间长?
开普勒第三定律
行星公转周期T与公转轨道半长轴a的关系?
水星 金星 地球 火星 木星 土星
周期(天) 87.97 225 365 687 4333 10759
半长轴(×106km) 57 108 149 228 778 1426
以你所学的数学知识,怎么更快地发现T与a的关系?
水星 金星 地球 火星 木星 土星
T2(年) 7738 50625 133225 471969 18774889 115756081
a3(×106km) 185193 1.26×106 3.3×106 1.18×107 4.71×108 2.90×109
a3/T2 3.36×1018 3.36×1018 3.36×1018 3.36×1018 3.36×1018 3.36×1018
开普勒第三定律
所有行星轨道的半长轴的三次方跟它的公转周期的二次方的比都相等。
开普勒第三定律也常说成周期定律
开普勒第三定律
k值与中心天体有关
中心天体既可以是恒星
也可以是行星
行星/卫星 半长轴(106km) 周期(天) k(m /s )
水星 57 87.97
金星 108 225
地球 149 365
火星 228 687
木星 778 4333
土星 1426 10759
天王星 2870 30660
海王星 4498 60148
月球 0.3844 27.3
同步卫星 0.0424 1
3.36×1018
3.36×1018
3.36×1018
3.36×1018
3.36×1018
3.36×1018
3.37×1018
3.37×1018
1.03×1013
1.03×1013
开普勒三定律
行星公转轨道可近似看做圆轨道
开普勒三定律
行星公转可近似看做匀速圆周运动
开普勒三定律
开普勒第三定律
转化为:
椭圆半长轴a
转变为圆的半径r
课堂小结
宇宙有没有中心?
