2023年中考数学一轮专题复习:几何图形初步与相交线、平行线学案(含答案)
文档属性
| 名称 | 2023年中考数学一轮专题复习:几何图形初步与相交线、平行线学案(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 216.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-05 16:37:09 | ||
图片预览

文档简介
2023年中考数学专题复习:几何图形初步与相交线、平行线
知识点梳理
1.直线:经过两点有一条直线,并且只有一条直线。简称:两点确定一条直线。
2.相交线:当两条不同的直线有一个公共点时,我们就称这两条直线相交。这个公共点叫做它们的交点。
3.两点的所有连线中,线段最短。 简称:两点之间,线段最短。
连接两点间的线段的长度,叫做这两点的距离。
4.线段的中点:线段上的一个点把线段分成相等的两条线段,这个点叫做线段的中点。
5.直线没有端点,向两方无限延伸,不可度量;射线有一个端点,向一方无限延伸,不可度量;线段有两个端点,不向任何一方延伸,能度量。
6.角:有公共端点的两条射线组成的图形叫做角。这个公共端点是角的顶点,两条射线是角的两条边。
7.角的度量:1°=60′ 1′=60″ (°、′、″分别是:度、分、秒)
8.角的分类:①锐角(0°< α < 90°)②直角(α = 90°)③钝角(90°< α < 180°)④平角(α =180°)⑤周角(α =360°)
9.角的平分线:从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线。
10.角平分线的性质:角的平分线上的点到角的两边的距离相等。角的内部到角的两边的距离相等的点在角的平分线上。
11.余角:一般地,如果两个角的和等于90°(直角),就说这两个角互为余角。
12.补角:如果两个角的和等于180°(平角),就说这两个角互为补角。
13.邻补角:有一条公共边,另一边互为反向延长线的两个角,叫做互为邻补角。
14.对顶角:有一个公共顶点,一个角的两边分别是另一个角的两边的反向延长线,这两个角叫做对顶角。
15.垂线:两直线相交所构成的四个角中有一个角是直角时,我们就说这两条直线互相垂直,其中一条直线叫做另外一条直线的垂线,它们的交点叫做垂足。
16.垂线性质:在同一平面内,过一点有且只有一条直线与已知直线垂直;连接直线外一点与直线上各点的所有线段中,垂线段最短。
17.点到直线的距离:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
18.平行线
(1)定义:在平面内不相交的两条直线叫做平行线。
(2)平行公理:经过直线外一点,有且只有一条直线与这条直线平行;如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
(3)平行线的性质
①两直线平行,同位角相等,内错角相等,同旁内角互补。
②两条平行线被第三条直线所截,同位角相等;
③两条平行线被第三条直线所截,内错角相等;
④两条平行线被第三条直线所截,同旁内角互补。
(4)平行线的判定
①同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行。
②两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行;
③两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行;
④两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
专题练习
选择题
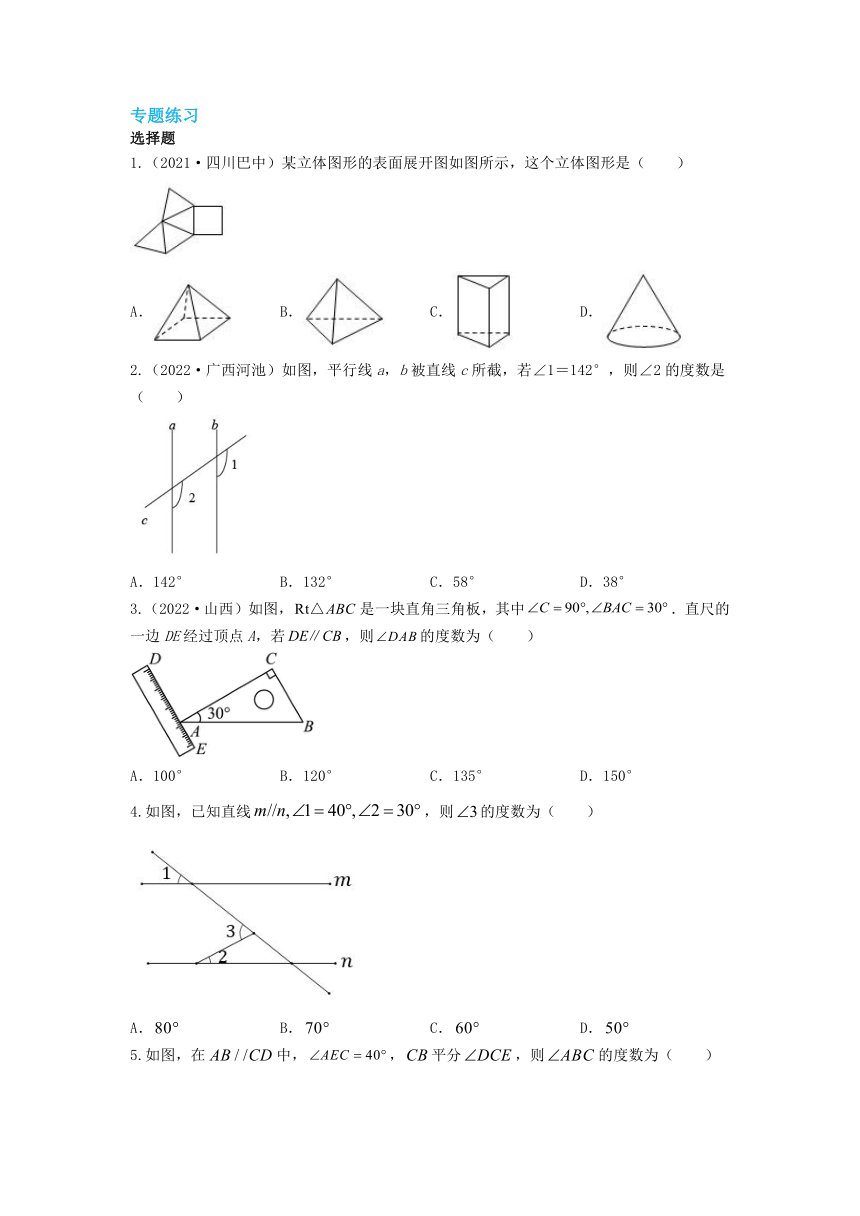
1.(2021·四川巴中)某立体图形的表面展开图如图所示,这个立体图形是( )
A. B. C. D.
2.(2022·广西河池)如图,平行线a,b被直线c所截,若∠1=142°,则∠2的度数是( )
A.142° B.132° C.58° D.38°
3.(2022·山西)如图,是一块直角三角板,其中.直尺的一边DE经过顶点A,若,则的度数为( )
A.100° B.120° C.135° D.150°
4.如图,已知直线,则的度数为( )
A. B. C. D.
5.如图,在中,,平分,则的度数为( )
A. B. C. D.
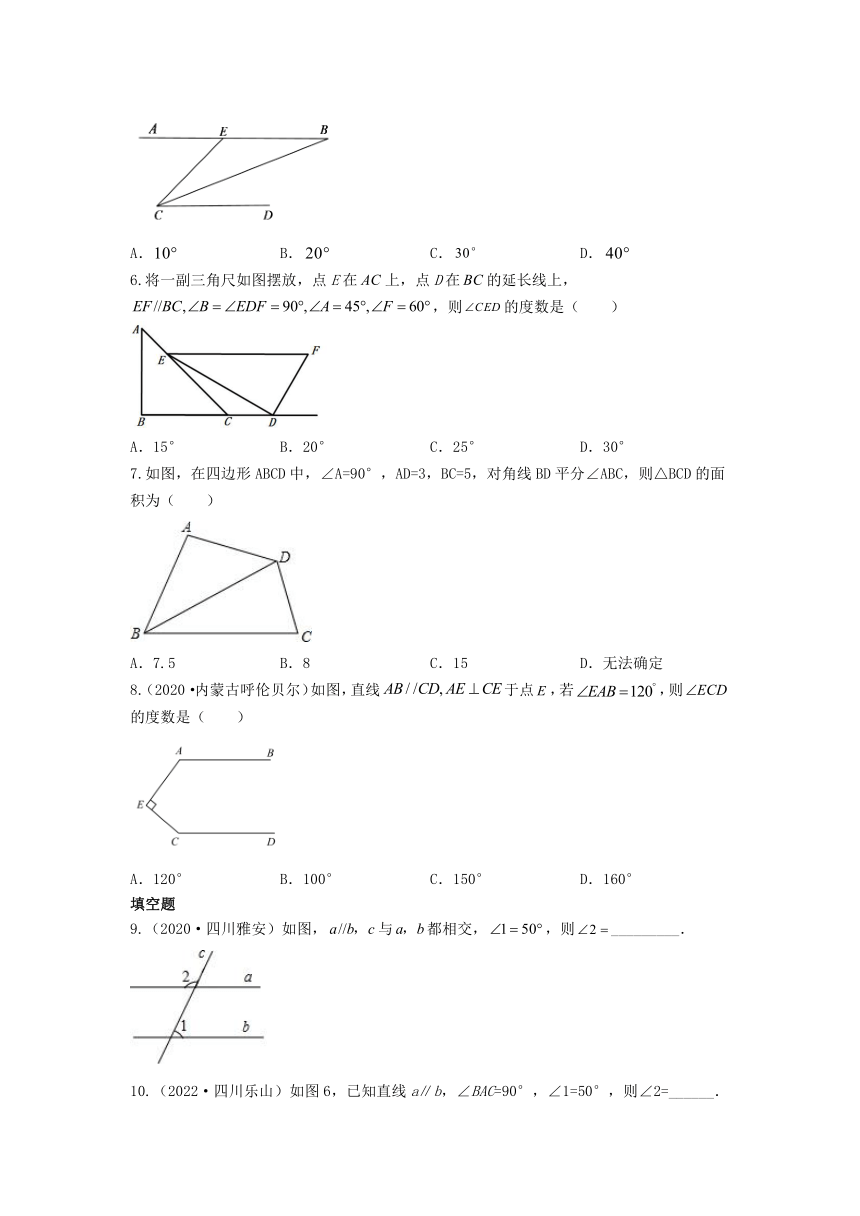
6.将一副三角尺如图摆放,点E在上,点D在的延长线上,,则的度数是( )
A.15° B.20° C.25° D.30°
7.如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )
A.7.5 B.8 C.15 D.无法确定
8.(2020·内蒙古呼伦贝尔)如图,直线于点,若,则的度数是( )
A.120° B.100° C.150° D.160°
填空题
9.(2020·四川雅安)如图,与都相交,,则_________.
10.(2022·四川乐山)如图6,已知直线a∥b,∠BAC=90°,∠1=50°,则∠2=______.
11.如图,在中,,,以点C为圆心,CA长为半径作弧,交直线BC于点P,连结AP,则的度数是_______.
12.(2021·湖北恩施)如图,已知,,,则__________.
13.(2021·江苏泰州)如图,木棒AB、CD与EF分别在G、H处用可旋转的螺丝铆住,∠EGB=100°,∠EHD=80°,将木棒AB绕点G逆时针旋转到与木棒CD平行的位置,则至少要旋转 °。
解答题
14.如图,方格纸中每个小正方形的边长均为1,线段AB和线段CD的端点均在小正方形的顶点上.
(1)在图中画出以AB为边的正方形ABEF,点E和点F均在小正方形的顶点上;
(2)在图中画出以CD为边的等腰三角形CDG,点G在小正方形的顶点上,且△CDG的周长为10.连接EG,请直接写出线段EG的长.
15.(2021·湖北武汉)如图,,,直线与,的延长线分别交于点,.求证:.
16.(2020·江苏镇江)如图,AC是四边形ABCD的对角线,∠1=∠B,点E、F分别在AB、BC上,BE=CD,BF=CA,连接EF.
(1)求证:∠D=∠2;
(2)若EF∥AC,∠D=78°,求∠BAC的度数.
参考答案:
1.A 2.A 3.B 4.B 5.B 6.A 7.A 8.C
9.130°
10.40°
11.或
12.30°
13.20
14.(1)如图,正方形ABEF即为所求.
(2)如图,△CDG即为所求.
15.证明:∵,
∴.
∵,
∴.
∴.
∴.
16.证明:(1)在△BEF和△CDA中,
,
∴△BEF≌△CDA(SAS),
∴∠D=∠2;
(2)∵∠D=∠2,∠D=78°,
∴∠D=∠2=78°,
∵EF∥AC,
∴∠2=∠BAC=78°.
知识点梳理
1.直线:经过两点有一条直线,并且只有一条直线。简称:两点确定一条直线。
2.相交线:当两条不同的直线有一个公共点时,我们就称这两条直线相交。这个公共点叫做它们的交点。
3.两点的所有连线中,线段最短。 简称:两点之间,线段最短。
连接两点间的线段的长度,叫做这两点的距离。
4.线段的中点:线段上的一个点把线段分成相等的两条线段,这个点叫做线段的中点。
5.直线没有端点,向两方无限延伸,不可度量;射线有一个端点,向一方无限延伸,不可度量;线段有两个端点,不向任何一方延伸,能度量。
6.角:有公共端点的两条射线组成的图形叫做角。这个公共端点是角的顶点,两条射线是角的两条边。
7.角的度量:1°=60′ 1′=60″ (°、′、″分别是:度、分、秒)
8.角的分类:①锐角(0°< α < 90°)②直角(α = 90°)③钝角(90°< α < 180°)④平角(α =180°)⑤周角(α =360°)
9.角的平分线:从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线。
10.角平分线的性质:角的平分线上的点到角的两边的距离相等。角的内部到角的两边的距离相等的点在角的平分线上。
11.余角:一般地,如果两个角的和等于90°(直角),就说这两个角互为余角。
12.补角:如果两个角的和等于180°(平角),就说这两个角互为补角。
13.邻补角:有一条公共边,另一边互为反向延长线的两个角,叫做互为邻补角。
14.对顶角:有一个公共顶点,一个角的两边分别是另一个角的两边的反向延长线,这两个角叫做对顶角。
15.垂线:两直线相交所构成的四个角中有一个角是直角时,我们就说这两条直线互相垂直,其中一条直线叫做另外一条直线的垂线,它们的交点叫做垂足。
16.垂线性质:在同一平面内,过一点有且只有一条直线与已知直线垂直;连接直线外一点与直线上各点的所有线段中,垂线段最短。
17.点到直线的距离:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
18.平行线
(1)定义:在平面内不相交的两条直线叫做平行线。
(2)平行公理:经过直线外一点,有且只有一条直线与这条直线平行;如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
(3)平行线的性质
①两直线平行,同位角相等,内错角相等,同旁内角互补。
②两条平行线被第三条直线所截,同位角相等;
③两条平行线被第三条直线所截,内错角相等;
④两条平行线被第三条直线所截,同旁内角互补。
(4)平行线的判定
①同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行。
②两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行;
③两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行;
④两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
专题练习
选择题
1.(2021·四川巴中)某立体图形的表面展开图如图所示,这个立体图形是( )
A. B. C. D.
2.(2022·广西河池)如图,平行线a,b被直线c所截,若∠1=142°,则∠2的度数是( )
A.142° B.132° C.58° D.38°
3.(2022·山西)如图,是一块直角三角板,其中.直尺的一边DE经过顶点A,若,则的度数为( )
A.100° B.120° C.135° D.150°
4.如图,已知直线,则的度数为( )
A. B. C. D.
5.如图,在中,,平分,则的度数为( )
A. B. C. D.
6.将一副三角尺如图摆放,点E在上,点D在的延长线上,,则的度数是( )
A.15° B.20° C.25° D.30°
7.如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )
A.7.5 B.8 C.15 D.无法确定
8.(2020·内蒙古呼伦贝尔)如图,直线于点,若,则的度数是( )
A.120° B.100° C.150° D.160°
填空题
9.(2020·四川雅安)如图,与都相交,,则_________.
10.(2022·四川乐山)如图6,已知直线a∥b,∠BAC=90°,∠1=50°,则∠2=______.
11.如图,在中,,,以点C为圆心,CA长为半径作弧,交直线BC于点P,连结AP,则的度数是_______.
12.(2021·湖北恩施)如图,已知,,,则__________.
13.(2021·江苏泰州)如图,木棒AB、CD与EF分别在G、H处用可旋转的螺丝铆住,∠EGB=100°,∠EHD=80°,将木棒AB绕点G逆时针旋转到与木棒CD平行的位置,则至少要旋转 °。
解答题
14.如图,方格纸中每个小正方形的边长均为1,线段AB和线段CD的端点均在小正方形的顶点上.
(1)在图中画出以AB为边的正方形ABEF,点E和点F均在小正方形的顶点上;
(2)在图中画出以CD为边的等腰三角形CDG,点G在小正方形的顶点上,且△CDG的周长为10.连接EG,请直接写出线段EG的长.
15.(2021·湖北武汉)如图,,,直线与,的延长线分别交于点,.求证:.
16.(2020·江苏镇江)如图,AC是四边形ABCD的对角线,∠1=∠B,点E、F分别在AB、BC上,BE=CD,BF=CA,连接EF.
(1)求证:∠D=∠2;
(2)若EF∥AC,∠D=78°,求∠BAC的度数.
参考答案:
1.A 2.A 3.B 4.B 5.B 6.A 7.A 8.C
9.130°
10.40°
11.或
12.30°
13.20
14.(1)如图,正方形ABEF即为所求.
(2)如图,△CDG即为所求.
15.证明:∵,
∴.
∵,
∴.
∴.
∴.
16.证明:(1)在△BEF和△CDA中,
,
∴△BEF≌△CDA(SAS),
∴∠D=∠2;
(2)∵∠D=∠2,∠D=78°,
∴∠D=∠2=78°,
∵EF∥AC,
∴∠2=∠BAC=78°.
同课章节目录
