二次根式[下学期]
图片预览



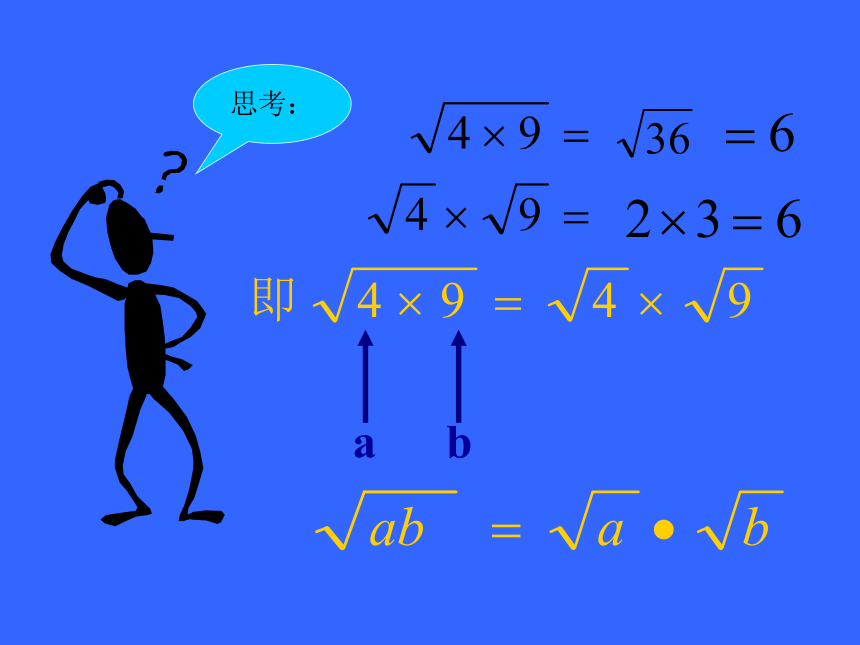




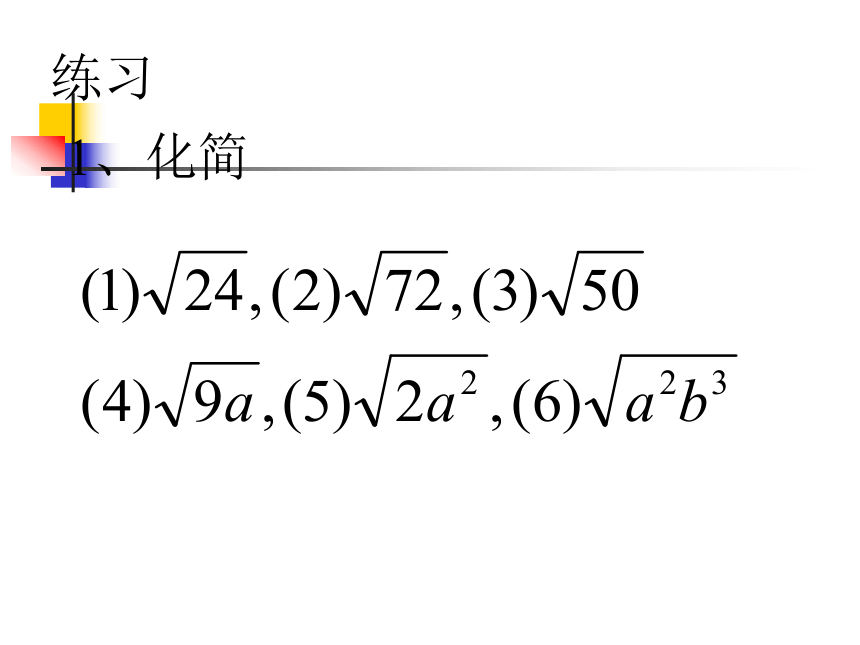
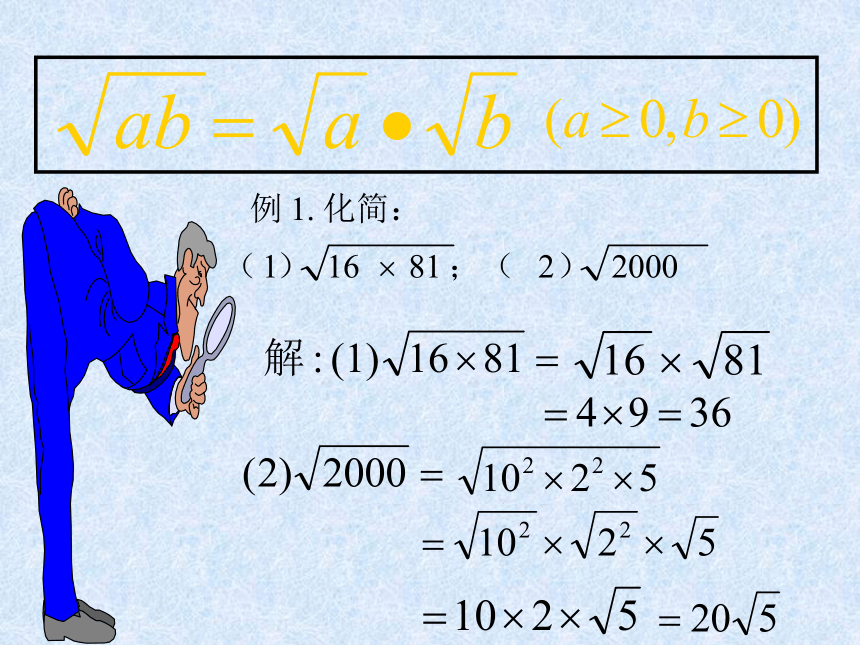

文档简介
课件32张PPT。16.2二次根式2.二次根式的乘法1、什么叫二次根式?下列
各式哪些是二次根式?哪些
不是?为什么?2、填空思考:ab积的算术平方根,
等于积中各因式的算术平方根.注意:a、b必须都是非负数!例题1、计算习题:如何化简二次根式关键:将被开方数因式分解或
因数分解,使出现“完全平方数”
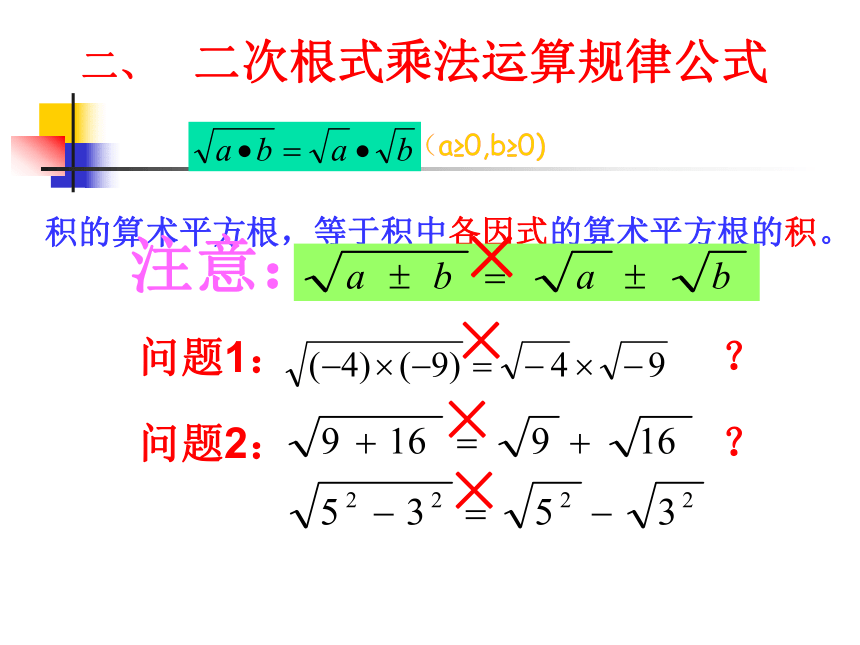
或“偶次方因式”例题2、化简练习1、化简第二课时二、 二次根式乘法运算规律公式积的算术平方根,等于积中各因式的算术平方根的积。问题1: ?×(a≥0,b≥0)问题2: ?×××注意:(a≥0,b≥0)例2. 化简:
(1) (2) 练习:
1.化简: (口答)
(1) (2)
(3) (4)16.2 二次根式的乘法 16.2 二次根式的乘法 2、化简二探讨:( )=(1)(2)观察1、2小题的结果,他们有什么特点?#(1)、(2)题结果相同。你能列出怎样的等式呢?即:这个等式用字母怎么表示呢?二次根式的除法思考:等式中的a和b有没有条件的限制?商的算术平方根等于被除式的算术平方根除以除式的算术平方根.请同学们用文字表达该等式。商的算术平方根:注意?(1) 这里的被开方数是一个整式.(可 以是多项式,也可以是单项式。) (2) 注意被开方数的取值范围。1、与积的算术平方根的性质比较:共同点:一个根号变成两个根号.区别:取值范围不同。商的算术平方根:2、理解和记忆商的算术平方根要注意的问题一例:化简:解:原式=练习:(填下列各题的解题步骤)解:原式==可以开方的一定要开方!化到最简!解:原式=遇到被开方数是小数先化成分数再化简! = =二:请你帮忙:小明在学习本节内容后,做一道化简题作业.第二天作业发下来后,小明知道做错了,可他百思不得其解,你能帮小明找出错的原因吗?解:原式=请大家从观察被开方数,想一想?分析:也就是说我们应该先把带分数化成假分数!再运用商的算术平方根的性质!很显然小明理解错带分数的意义正确解法:解:原式=总结:遇到被开方数是带分数,化带分数为假分数训练题:三:例这里a,b都为整式,直接运用性质。解:原式=练习一:解: 练习单元一:( ) ( )总结:商的算术平方根性质的运用一定要注意被开方数的取值范围。错C二:选择:( ) D三:思考( )B所以本题选B分析:要求 关键是求X、Y,
两个非负数相加和为0。也就是说它们要分别为0。解得:例2、把下列各式的化简: 2.计算(所有字母都是正数)
各式哪些是二次根式?哪些
不是?为什么?2、填空思考:ab积的算术平方根,
等于积中各因式的算术平方根.注意:a、b必须都是非负数!例题1、计算习题:如何化简二次根式关键:将被开方数因式分解或
因数分解,使出现“完全平方数”
或“偶次方因式”例题2、化简练习1、化简第二课时二、 二次根式乘法运算规律公式积的算术平方根,等于积中各因式的算术平方根的积。问题1: ?×(a≥0,b≥0)问题2: ?×××注意:(a≥0,b≥0)例2. 化简:
(1) (2) 练习:
1.化简: (口答)
(1) (2)
(3) (4)16.2 二次根式的乘法 16.2 二次根式的乘法 2、化简二探讨:( )=(1)(2)观察1、2小题的结果,他们有什么特点?#(1)、(2)题结果相同。你能列出怎样的等式呢?即:这个等式用字母怎么表示呢?二次根式的除法思考:等式中的a和b有没有条件的限制?商的算术平方根等于被除式的算术平方根除以除式的算术平方根.请同学们用文字表达该等式。商的算术平方根:注意?(1) 这里的被开方数是一个整式.(可 以是多项式,也可以是单项式。) (2) 注意被开方数的取值范围。1、与积的算术平方根的性质比较:共同点:一个根号变成两个根号.区别:取值范围不同。商的算术平方根:2、理解和记忆商的算术平方根要注意的问题一例:化简:解:原式=练习:(填下列各题的解题步骤)解:原式==可以开方的一定要开方!化到最简!解:原式=遇到被开方数是小数先化成分数再化简! = =二:请你帮忙:小明在学习本节内容后,做一道化简题作业.第二天作业发下来后,小明知道做错了,可他百思不得其解,你能帮小明找出错的原因吗?解:原式=请大家从观察被开方数,想一想?分析:也就是说我们应该先把带分数化成假分数!再运用商的算术平方根的性质!很显然小明理解错带分数的意义正确解法:解:原式=总结:遇到被开方数是带分数,化带分数为假分数训练题:三:例这里a,b都为整式,直接运用性质。解:原式=练习一:解: 练习单元一:( ) ( )总结:商的算术平方根性质的运用一定要注意被开方数的取值范围。错C二:选择:( ) D三:思考( )B所以本题选B分析:要求 关键是求X、Y,
两个非负数相加和为0。也就是说它们要分别为0。解得:例2、把下列各式的化简: 2.计算(所有字母都是正数)
