【全国百强校】江西省师大附中2013-2014学年高中数学必修二《平面与平面平行的判定(二)》教学课件(北师大版)
文档属性
| 名称 | 【全国百强校】江西省师大附中2013-2014学年高中数学必修二《平面与平面平行的判定(二)》教学课件(北师大版) |

|
|
| 格式 | zip | ||
| 文件大小 | 74.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-06-27 00:00:00 | ||
图片预览





文档简介
课件15张PPT。平面与平面平行的判定江西师大附中 蔡卫强2.两个平面平行的基本特征是什么?
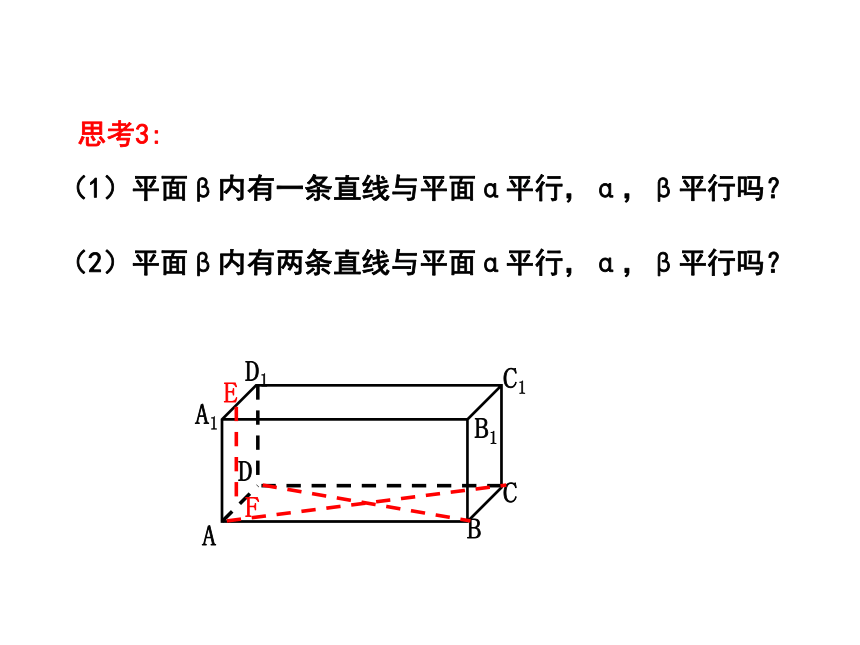
有什么简单办法判定两个平面平行呢?思考1:根据定义,判定平面与平面平行的关键是什么?思考2: 若一个平面内的所有直线都与另一个平面平行,那么这两个平面的位置关系怎样?若一个平面内有一条直线与另一个平面有公共点,那么这两个平面的位置关系又会怎样呢?(1)平面β内有一条直线与平面α平行,α,β平行吗?(2)平面β内有两条直线与平面α平行,α,β平行吗?思考3:思考4: 建筑师如何检验屋顶平面与水平面是否平行?思考5:通过上述分析,我们可以得到判定平面与平面平行的一个定理,你能用文字语言表述出该定理的内容吗?定理 一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.
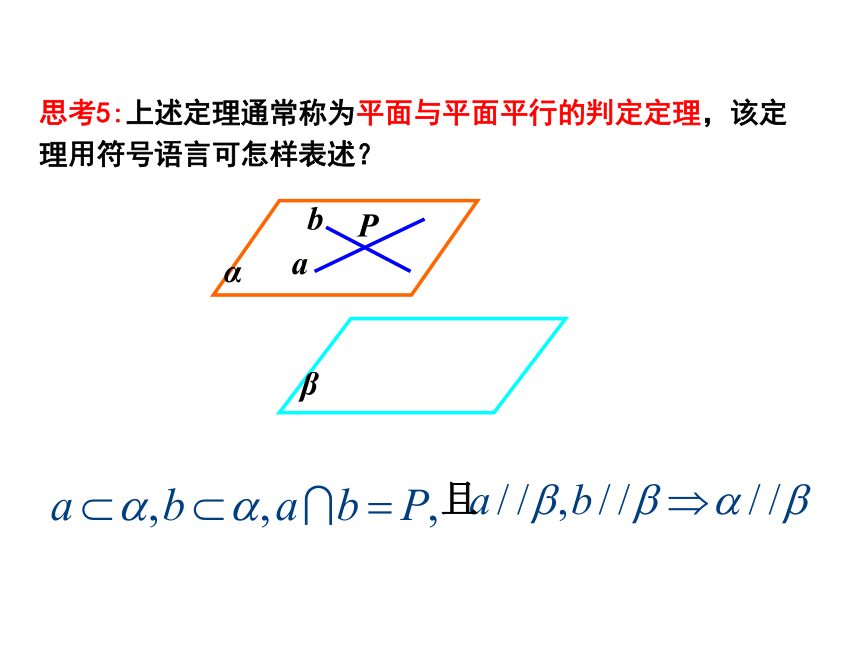
思考5:上述定理通常称为平面与平面平行的判定定理,该定理用符号语言可怎样表述?且思考5:在平面与平面平行的判定定理中,“a∥β,b∥β” ,可用什么条件替代?由此可得什么推论?推论 如果一个平面内有两条相交直线分别平行于另一个平面内的两条直线,那么这两个平面平行. 例题分析证明: 四边形是平行四边形
.例1、已知正方体ABCD-A1B1C1D1,求证:平面AB1D1∥平面C1BD。例2 在三棱锥P-ABC中,点D、E、F分别是△PAB、△PBC、△PAC的重心,求证:平面DEF//平面ABC.∵点D、E、F分别是△PAB、△PBC、△PAC的重心,
G证明:连PD,PE,PF并延长,分别交AB,BC,AC于点M,N,G,连MN,MG,NG,∴PD:DM=PE:EN=PF:FG=2:1,∴DE∥MN,DF∥MG,∴ DE//平面ABC,DF//平面ABC,又DE∩DF=D, ∴平面DEF//平面ABC
棱长为a的正方体AC1中,设M、N、E、F分别为棱A1B1、A1D1、 C1D1、 B1C1的中点.(1)求证:E、F、B、D四点共面;(2)求证:面AMN∥面EFBD.随堂练习证明:(1)连 B1D1,∵E、F分别为棱 C1D1,B1C1的中点, ∴EF∥B1D1∥BD
∴ E、F、B、D四点共面(2)∵M、N、E、F分别为棱A1B1、A1D1、C1D1、 B1C1的中点.∴ MN ∥ B1D1∥EF ,∴ MN∥面EFBD,
连EM,则ME ∥ A1D1∥ AD,∴四边形ADEM为平行四边形,∴AM∥DE, ∴ AM∥面EFBD,
又AM∩MN=M, ∴面AMN∥面EFBD.
小结:1.证明平面与平面平行的方法:(1)利用定义;(2)利用判定定理.2.数学思想方法:转化的思想知识小结平面与平面没有公共点线线平行作业 P31 练习:4.
P34 习题1-5
A组:4.
B组:1.谢谢大家!
有什么简单办法判定两个平面平行呢?思考1:根据定义,判定平面与平面平行的关键是什么?思考2: 若一个平面内的所有直线都与另一个平面平行,那么这两个平面的位置关系怎样?若一个平面内有一条直线与另一个平面有公共点,那么这两个平面的位置关系又会怎样呢?(1)平面β内有一条直线与平面α平行,α,β平行吗?(2)平面β内有两条直线与平面α平行,α,β平行吗?思考3:思考4: 建筑师如何检验屋顶平面与水平面是否平行?思考5:通过上述分析,我们可以得到判定平面与平面平行的一个定理,你能用文字语言表述出该定理的内容吗?定理 一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.
思考5:上述定理通常称为平面与平面平行的判定定理,该定理用符号语言可怎样表述?且思考5:在平面与平面平行的判定定理中,“a∥β,b∥β” ,可用什么条件替代?由此可得什么推论?推论 如果一个平面内有两条相交直线分别平行于另一个平面内的两条直线,那么这两个平面平行. 例题分析证明: 四边形是平行四边形
.例1、已知正方体ABCD-A1B1C1D1,求证:平面AB1D1∥平面C1BD。例2 在三棱锥P-ABC中,点D、E、F分别是△PAB、△PBC、△PAC的重心,求证:平面DEF//平面ABC.∵点D、E、F分别是△PAB、△PBC、△PAC的重心,
G证明:连PD,PE,PF并延长,分别交AB,BC,AC于点M,N,G,连MN,MG,NG,∴PD:DM=PE:EN=PF:FG=2:1,∴DE∥MN,DF∥MG,∴ DE//平面ABC,DF//平面ABC,又DE∩DF=D, ∴平面DEF//平面ABC
棱长为a的正方体AC1中,设M、N、E、F分别为棱A1B1、A1D1、 C1D1、 B1C1的中点.(1)求证:E、F、B、D四点共面;(2)求证:面AMN∥面EFBD.随堂练习证明:(1)连 B1D1,∵E、F分别为棱 C1D1,B1C1的中点, ∴EF∥B1D1∥BD
∴ E、F、B、D四点共面(2)∵M、N、E、F分别为棱A1B1、A1D1、C1D1、 B1C1的中点.∴ MN ∥ B1D1∥EF ,∴ MN∥面EFBD,
连EM,则ME ∥ A1D1∥ AD,∴四边形ADEM为平行四边形,∴AM∥DE, ∴ AM∥面EFBD,
又AM∩MN=M, ∴面AMN∥面EFBD.
小结:1.证明平面与平面平行的方法:(1)利用定义;(2)利用判定定理.2.数学思想方法:转化的思想知识小结平面与平面没有公共点线线平行作业 P31 练习:4.
P34 习题1-5
A组:4.
B组:1.谢谢大家!
