第一章 空间向量与立体几何 章末复习 课件(共45张PPT)
文档属性
| 名称 | 第一章 空间向量与立体几何 章末复习 课件(共45张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-04 21:33:09 | ||
图片预览










文档简介
(共45张PPT)
空间向量与立体几何
几类特殊的空间向量
名称 定义及表示
零向量 规定长度为0的向量叫_______,记为0
单位向量 ______的向量叫单位向量
相反向量 与向量a长度_____而方向_____的向量,称为a的相反向量,记为-a
相等向量 方向_____且模_____的向量称为相等向量,_____且_____的有向线段表示同一向量或相等向量
零向量
模为1
相等
相反
相同
相等
同向
等长
平面向量/
加法
减法
数乘
运算
运
算
律
减法:三角形法则
加法:三角形法则或平行四边形法则
空间向量
数乘:ka,k为正数,负数,零
加法交换律
加法结合律
数乘分配律
空间向量的线性运算
由于任意两个空间向量都可以通过平移转化为同一平面内的向量,任意两个空间向量的运算就可以转化为平面向量的运算.
证明?
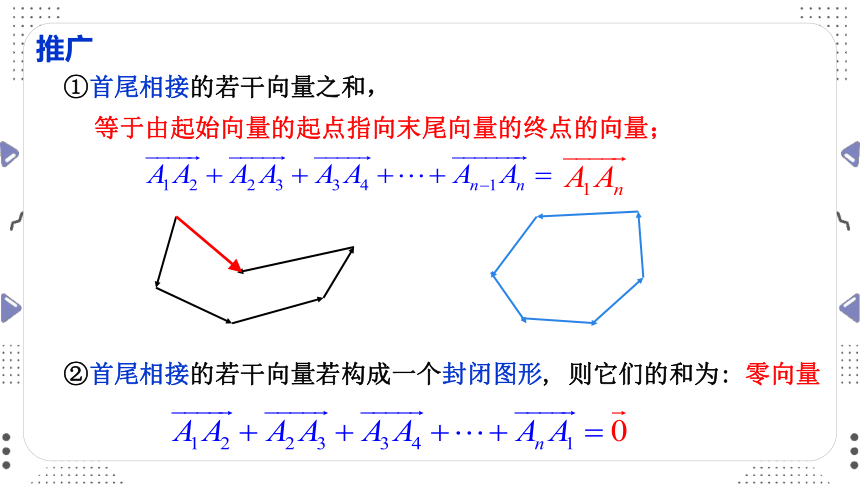
推广
①首尾相接的若干向量之和,
②首尾相接的若干向量若构成一个封闭图形, 则它们的和为:
等于由起始向量的起点指向末尾向量的终点的向量;
零向量
(1)实数与向量的积
与平面向量一样,实数λ与空间向量a的乘积λa仍然是一个向量,称为向量的数乘运算,记作λa,其长度和方向规定如下:
①|λa|=____.
②当λ>0时,λa与向量a方向相同;当λ<0时,λa与向量a方向 ;当λ=0时,λa=0.
(2)空间向量数乘运算满足以下运算律
①λ(μa)=______; ②λ(a+b)=________;
③(λ1+λ2)a=_________(拓展).
相反
|λ||a|
(λμ)a
λa+λb
λ1a+λ2a
空间向量的数乘运算
两个向量数量积的性质 ①若a,b是非零向量,则a⊥b _______
②若a与b同向,则a·b=______;若反向,则a·b=________.
特别地,a·a=____或|a|=
③若θ为a,b的夹角,则cos θ=_______
④|a·b|≤|a|·|b|
空间向量的数量积的性质
a·b=0
|a|·|b|
-|a|·|b|
|a|2
A
B
(1)
(2)
(3)
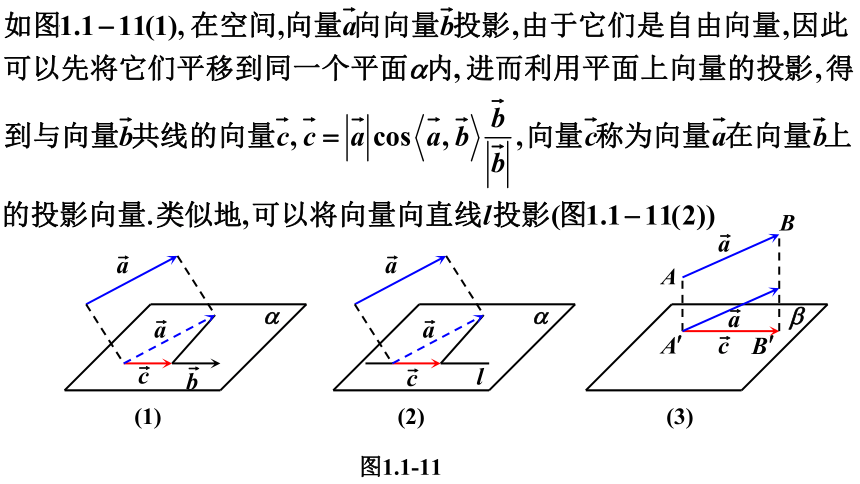
图1.1-11
空间向量的共线(平行)的 充要条件
零向量与任意向量共线
(1)共线向量:如果表示空间向量的有向线段所在直线互相平行或重合,则这些向量叫做共线向量(或平行向量),记作
(2)共线向量定理:
(类比平面向量共线充要条件)
共面向量定理:
空间向量的共面充要条件
设u1,u2分别是直线l1,l2的方向向量,n1,n2分别是平面α,β的法向量.
线线平行 l1∥l2 _________ ____________________
线面平行 l1∥α ______________ ________________
面面平行 α∥β ______________ ________________
线线垂直 l1⊥l2 _____________ ________________
线面垂直 l1⊥α ______________ ________________
面面垂直 α⊥β ______________ _____________
1.点到直线的距离(勾股定理)-平行线间的距离
2.点P到平面α的距离-平行线面、平行平面间的距离
距离问题
P
A
Q
D
A
Q
P
法1
法2
等体积法
3.异面直线公垂线的长
(点到平面的距离)
先求直线AC,BD的公垂线的方向向量
再在直线上各找一点,如
则
A
D
C
B
N
M
Q
夹角问题
线线角θ:
线面角θ:
面面角θ:
二面角θ:
空间向量与立体几何
几类特殊的空间向量
名称 定义及表示
零向量 规定长度为0的向量叫_______,记为0
单位向量 ______的向量叫单位向量
相反向量 与向量a长度_____而方向_____的向量,称为a的相反向量,记为-a
相等向量 方向_____且模_____的向量称为相等向量,_____且_____的有向线段表示同一向量或相等向量
零向量
模为1
相等
相反
相同
相等
同向
等长
平面向量/
加法
减法
数乘
运算
运
算
律
减法:三角形法则
加法:三角形法则或平行四边形法则
空间向量
数乘:ka,k为正数,负数,零
加法交换律
加法结合律
数乘分配律
空间向量的线性运算
由于任意两个空间向量都可以通过平移转化为同一平面内的向量,任意两个空间向量的运算就可以转化为平面向量的运算.
证明?
推广
①首尾相接的若干向量之和,
②首尾相接的若干向量若构成一个封闭图形, 则它们的和为:
等于由起始向量的起点指向末尾向量的终点的向量;
零向量
(1)实数与向量的积
与平面向量一样,实数λ与空间向量a的乘积λa仍然是一个向量,称为向量的数乘运算,记作λa,其长度和方向规定如下:
①|λa|=____.
②当λ>0时,λa与向量a方向相同;当λ<0时,λa与向量a方向 ;当λ=0时,λa=0.
(2)空间向量数乘运算满足以下运算律
①λ(μa)=______; ②λ(a+b)=________;
③(λ1+λ2)a=_________(拓展).
相反
|λ||a|
(λμ)a
λa+λb
λ1a+λ2a
空间向量的数乘运算
两个向量数量积的性质 ①若a,b是非零向量,则a⊥b _______
②若a与b同向,则a·b=______;若反向,则a·b=________.
特别地,a·a=____或|a|=
③若θ为a,b的夹角,则cos θ=_______
④|a·b|≤|a|·|b|
空间向量的数量积的性质
a·b=0
|a|·|b|
-|a|·|b|
|a|2
A
B
(1)
(2)
(3)
图1.1-11
空间向量的共线(平行)的 充要条件
零向量与任意向量共线
(1)共线向量:如果表示空间向量的有向线段所在直线互相平行或重合,则这些向量叫做共线向量(或平行向量),记作
(2)共线向量定理:
(类比平面向量共线充要条件)
共面向量定理:
空间向量的共面充要条件
设u1,u2分别是直线l1,l2的方向向量,n1,n2分别是平面α,β的法向量.
线线平行 l1∥l2 _________ ____________________
线面平行 l1∥α ______________ ________________
面面平行 α∥β ______________ ________________
线线垂直 l1⊥l2 _____________ ________________
线面垂直 l1⊥α ______________ ________________
面面垂直 α⊥β ______________ _____________
1.点到直线的距离(勾股定理)-平行线间的距离
2.点P到平面α的距离-平行线面、平行平面间的距离
距离问题
P
A
Q
D
A
Q
P
法1
法2
等体积法
3.异面直线公垂线的长
(点到平面的距离)
先求直线AC,BD的公垂线的方向向量
再在直线上各找一点,如
则
A
D
C
B
N
M
Q
夹角问题
线线角θ:
线面角θ:
面面角θ:
二面角θ:
