普陀区2013-2014学年度第二学期初中七年级数学期末质量调研试卷(含答案)
文档属性
| 名称 | 普陀区2013-2014学年度第二学期初中七年级数学期末质量调研试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 131.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-06-26 21:13:59 | ||
图片预览



文档简介
普陀区2013学年度第二学期初中七年级数学期末质量调研
题 号 一 二 三 四 五 总 分
得 分
考生注意:1.本试卷含五个大题,共26题;
2.除第一、二大题外,其余各题如无特别说明,都必须写出解题的主要步骤.
一.填空(本大题共有14题,每题2分,满分28分)
1.6的平方根是 .
2.求值: .
3.如果,则x= .
4.比较大小:-5 (填“>”、“=”或“<”).
5.用幂的形式表示:= .
6.今年“五一”小长假从4月30日至5月 ( http: / / www.21cnjy.com )3日共计4天,铁路上海站迎来客流出行高峰,四天共计发送旅客逾1300000人次,1300000用科学记数法表示为 (保留3个有效数字).
7.如图,已知点B、C、E在一直线上,且∠1=∠B,那么 ∥ .
(第7题图) (第9题图) (第10题图)
8.一个三角形的三个内角的度数比是2∶3∶4,这个三角形是 三角形(按角分类).
9.如图,直线a∥b,把三角板的直角顶点放在直线b上,如果∠2=35°,那么
∠1= °.
10.如图,已知∠ACB=∠F,BE=CF,添加一个合适的条件,如 ,就可说明△ABC≌△DEF.
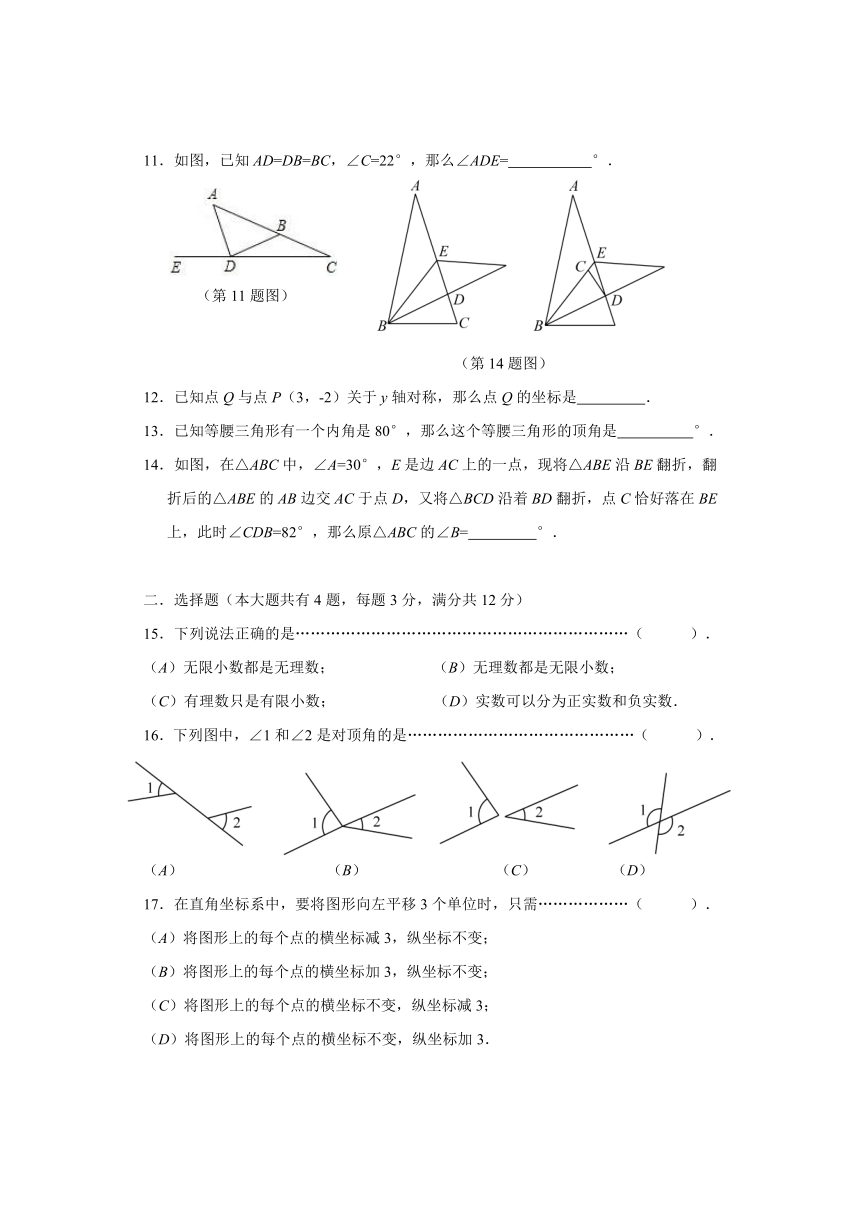
11.如图,已知AD=DB=BC,∠C=22°,那么∠ADE= °.
(第11题图)
(第14题图)
12.已知点Q与点P(3,-2)关于y轴对称,那么点Q的坐标是 .
13.已知等腰三角形有一个内角是80°,那么这个等腰三角形的顶角是 °.
14.如图,在△ABC中,∠A=30°,E ( http: / / www.21cnjy.com )是边AC上的一点,现将△ABE沿BE翻折,翻折后的△ABE的AB边交AC于点D,又将△BCD沿着BD翻折,点C恰好落在BE上,此时∠CDB=82°,那么原△ABC的∠B= °.
二.选择题(本大题共有4题,每题3分,满分共12分)
15.下列说法正确的是…………………………………………………………( ).
(A)无限小数都是无理数; (B)无理数都是无限小数;
(C)有理数只是有限小数; (D)实数可以分为正实数和负实数.
16.下列图中,∠1和∠2是对顶角的是………………………………………( ).
(A) (B) (C) (D)
17.在直角坐标系中,要将图形向左平移3个单位时,只需………………( ).
(A)将图形上的每个点的横坐标减3,纵坐标不变;
(B)将图形上的每个点的横坐标加3,纵坐标不变;
(C)将图形上的每个点的横坐标不变,纵坐标减3;
(D)将图形上的每个点的横坐标不变,纵坐标加3.
18.有四根细木棒,长度分别为3cm,5c ( http: / / www.21cnjy.com )m,7cm,9cm,现任取其中的三根木棒,组成一个三角形,问:有几种可能?…………………………………………( ).
(A)1种; (B)2种; (C)3种; (D)4种.
三、(本大题共有3题,每小题各6分,满分18分)
19.计算:.
20.计算:.
21.画图:已知线段a、b.
(1)画△ABC,使AB=a,BC=b,∠B=45°;
(2)画出(1)中△ABC的角平分线AD;
(3)过点D作DE⊥AB,垂足为点E,如果点D到直线AB的垂线段的长度为1.7,那么点D到直线AC的距离为 .
四、(本大题共有5题,第22、23题各6分,第24题 8分,第25题10分,满分30分)
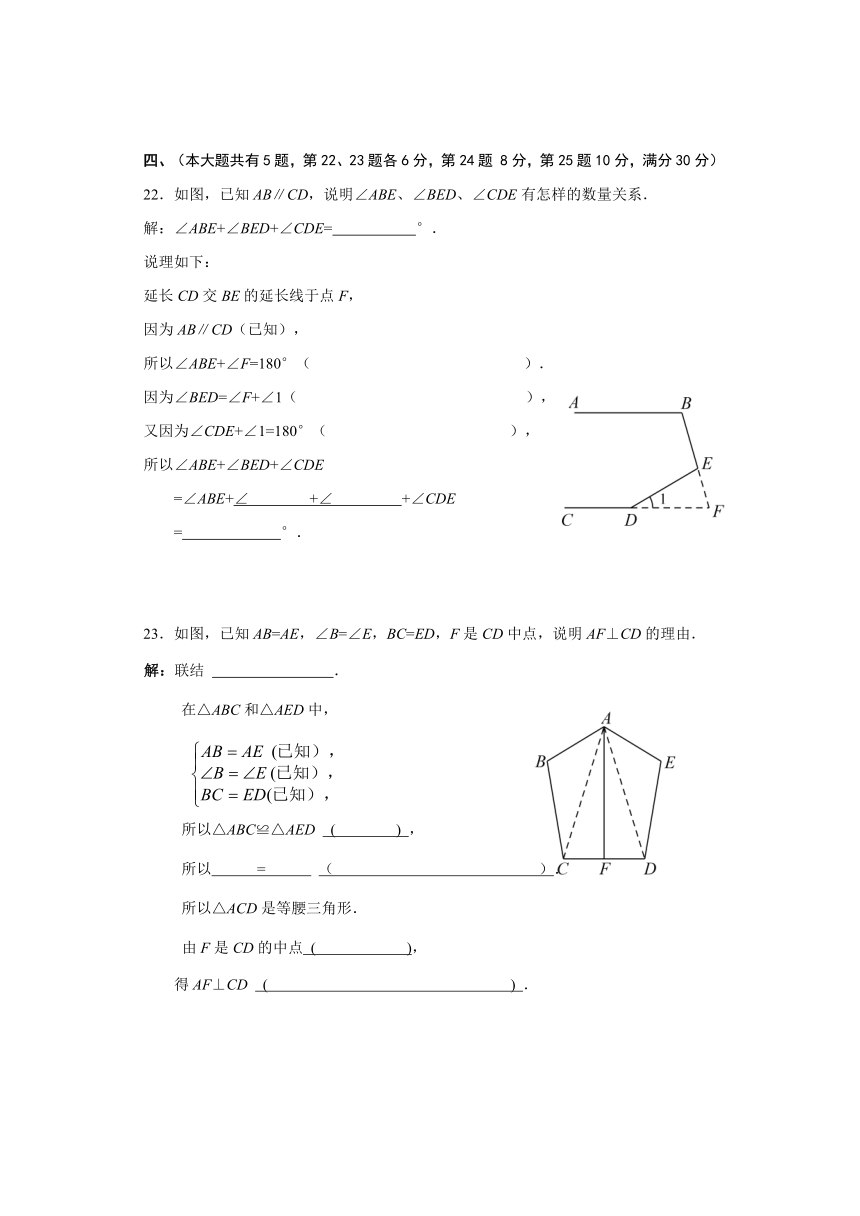
22.如图,已知AB∥CD,说明∠ABE、∠BED、∠CDE有怎样的数量关系.
解:∠ABE+∠BED+∠CDE= °.
说理如下:
延长CD交BE的延长线于点F,
因为AB∥CD(已知),
所以∠ABE+∠F=180°( ).
因为∠BED=∠F+∠1( ),
又因为∠CDE+∠1=180°( ),
所以∠ABE+∠BED+∠CDE
=∠ABE+∠ +∠ +∠CDE
= °.
23.如图,已知AB=AE,∠B=∠E,BC=ED,F是CD中点,说明AF⊥CD的理由.
解:联结 .
在△ABC和△AED中,
HYPERLINK "http://www.21cnjy.com"
所以△ABC≌△AED ( ) ,
所以 = ( ).
所以△ACD是等腰三角形.
由F是CD的中点 ( ),
得AF⊥CD ( ) .
24.如图,在△ABC中, ( http: / / www.21cnjy.com )已知AD平分∠BAC,E是边AB上的一点,AE=AC,F是边AC上的一点,联结DE、CE、FE,当EC平分∠DEF时,猜测EF、BC的位置关系,并说明理由.
解:、的位置关系是 .
说理如下:
因为是的角平分线(已知)
所以.
在△和△中,
HYPERLINK "http://www.21cnjy.com"
所以△≌△().
得 (全等三角形的对应边相等).
(完成以下说理过程)
25.如图,等边△ABC,点P在△ABC内,点Q在△ABC外,分别联结AP、BP、AQ、CQ,∠ABP=∠ACQ,BP=CQ.
(1)说明△ABP≌△ACQ;
(2)联结PQ,说明△APQ是等边三角形;
(3)联结PC,设△CPQ是以∠PQC为顶角的等腰三角形,且∠BPC=100°,求∠APB的度数.
26.如图,在平面直角坐标系中,点A的坐标为(-2,0),点B的坐标为(0,n),以点B为直角顶点,点C在第二象限内,作等腰直角△ABC.
(1)求点C的坐标(用字母n表示)(提示:过点C作y轴的垂线)
(2)如果△ABC的面积为5.5,求n的值;
(3)在(2)的条件下,坐标平面内是否 ( http: / / www.21cnjy.com )存在一点M,使以点M、A、B为顶点组成的三角形与△ABC全等?如果存在画出符合要求的图形,并直接写出点M的坐标.
(第26题图) (第26题备用图)
普陀区2013学年度第二学期初中七年级数学期末质量调研
参考答案与评分意见2014.6
一、填空题(本大题共有14题,每题2分,满分28分)
1.; 2.; 3.; 4.<; 5.; 6.;
7. DC// AB; 8.锐角; 9.55° 10.∠A=∠D或∠DEF=∠B或;
11.66°; 12.; 13.80°或20°; 14.78°.
二、单项选择题(本大题共有4题,每题3分,满分共12分)
15.B; 16.D ; 17.A; 18.C.
三、(本大题共有3题,每小题各6分,满分18分)
19.解:原式=………………………………………(3分)
=…………………………………………………………(2分)
=.……………………………………………………………(1分)
20.解: 原式= ………………………………………………(2分)
= ………………………………………………… (2分)
= …………………………………………………………(1分)
=9. ……………………………………………………………(1分)
21.(1)画图正确2分………………………………………………………………(2分)
结论1分……………………………………………………………………(1分)
(2)画图正确……………………………………………………………………(1分)
(3)点D到直线AC的距离为1.7. …………………………………………(2分)
四、(本大题共有5题,第22、23题各6分,第24题 8分,第25题10分,满分30分)
22.解: 360°, ……………………………………………………………………(1分)
两直线平行,同旁内角互补.……………………………………………(1分)
三角形的一个外角等于与它不相邻的两个内角的和,…………………(1分)
邻补角的意义或平角意义, ……………………………………………(1分)
∠F+∠1 , …………………………………………………………………(1分)
360°.………………………………………………………………………(1分)
23.解:联结 AC、AD . …………………………………………………………(1分)
在△ABC和△AED中,
HYPERLINK "http://www.21cnjy.com"
所以△ABC≌△AED ( S.A S. ) ,……………………………………………(1分)
所以 AC = AD (全等三角形的对应边相等).…………………(1分+1分)
所以△ACD是等腰三角形 .
又因为F是CD的中点 ( 已知 ),…………………………………………(1分)
所以AF⊥CD ( 等腰三角形的三线合一 ) .………………………………(1分)
24.解:、的位置关系是 EF∥BC .……………………………(1分)
理由如下:
因为是的角平分线(已知)
所以.
在△和△中,
HYPERLINK "http://www.21cnjy.com" …………………………………………………(1分+1分)
所以△≌△().
得 DE =DC (全等三角形的对应边相等).……………………………(1分)
所以.……………………………………………………………………(1分)
因为平分(已知),
所以.……………………………………………………………………(1分)
得.………………………………………………………………………(1分)
所以EF∥BC(内错角相等,两直线平行).………………………………(1分)
( http: / / www.21cnjy.com )
25.解:(1)因为△ABC是等边三角形(已知),
所以AB=AC,∠BAC=60°(等边三角形的性质).……………… (2分)
在△和△中,
HYPERLINK "http://www.21cnjy.com"
所以△≌△(S.A.S).……………………(1分)
(2)因为△≌△,
所以,∠1=∠2(全等三角形的对应边、对应角相等).……(1分)
因为∠1+∠3=60°,
所以∠2+∠3=60°.…………………………………………………………(1分)
即.
所以△是等边三角形(有一个角是60°的等腰三角形是等边三角形).( 1分)
(3)因为△≌△,
所以(全等三角形的对应角相等).(1分)
设,
那么.
因为△是等边三角形,
所以.
得.
因为,
所以(等边对等角).……………………………………… (1分)
因为(三角形的内角和等于180o),
所以.
因为,
又因为,
所以.……………………………………… (1分)
解得.………………………………………………………………(1分)
所以为.
26.解:
(1)过点作轴的垂线CH,垂足为H,
得.
因为△是等腰直角三角形,
所以,.…(1分)
又因为,
所以.
在△和△中,
HYPERLINK "http://www.21cnjy.com"
所以△≌△().……………………………………………(1分)
所以, .
点的坐标是.……………(1分+1分)(横坐标、纵坐标各1分)
(2),………………………………(1分)
(负值已舍)………………………………………………(1分)
(3)(每个点及其坐标2分,其中点的位置1分,坐标1分)
a
b
C
B
A
C
B
A
题 号 一 二 三 四 五 总 分
得 分
考生注意:1.本试卷含五个大题,共26题;
2.除第一、二大题外,其余各题如无特别说明,都必须写出解题的主要步骤.
一.填空(本大题共有14题,每题2分,满分28分)
1.6的平方根是 .
2.求值: .
3.如果,则x= .
4.比较大小:-5 (填“>”、“=”或“<”).
5.用幂的形式表示:= .
6.今年“五一”小长假从4月30日至5月 ( http: / / www.21cnjy.com )3日共计4天,铁路上海站迎来客流出行高峰,四天共计发送旅客逾1300000人次,1300000用科学记数法表示为 (保留3个有效数字).
7.如图,已知点B、C、E在一直线上,且∠1=∠B,那么 ∥ .
(第7题图) (第9题图) (第10题图)
8.一个三角形的三个内角的度数比是2∶3∶4,这个三角形是 三角形(按角分类).
9.如图,直线a∥b,把三角板的直角顶点放在直线b上,如果∠2=35°,那么
∠1= °.
10.如图,已知∠ACB=∠F,BE=CF,添加一个合适的条件,如 ,就可说明△ABC≌△DEF.
11.如图,已知AD=DB=BC,∠C=22°,那么∠ADE= °.
(第11题图)
(第14题图)
12.已知点Q与点P(3,-2)关于y轴对称,那么点Q的坐标是 .
13.已知等腰三角形有一个内角是80°,那么这个等腰三角形的顶角是 °.
14.如图,在△ABC中,∠A=30°,E ( http: / / www.21cnjy.com )是边AC上的一点,现将△ABE沿BE翻折,翻折后的△ABE的AB边交AC于点D,又将△BCD沿着BD翻折,点C恰好落在BE上,此时∠CDB=82°,那么原△ABC的∠B= °.
二.选择题(本大题共有4题,每题3分,满分共12分)
15.下列说法正确的是…………………………………………………………( ).
(A)无限小数都是无理数; (B)无理数都是无限小数;
(C)有理数只是有限小数; (D)实数可以分为正实数和负实数.
16.下列图中,∠1和∠2是对顶角的是………………………………………( ).
(A) (B) (C) (D)
17.在直角坐标系中,要将图形向左平移3个单位时,只需………………( ).
(A)将图形上的每个点的横坐标减3,纵坐标不变;
(B)将图形上的每个点的横坐标加3,纵坐标不变;
(C)将图形上的每个点的横坐标不变,纵坐标减3;
(D)将图形上的每个点的横坐标不变,纵坐标加3.
18.有四根细木棒,长度分别为3cm,5c ( http: / / www.21cnjy.com )m,7cm,9cm,现任取其中的三根木棒,组成一个三角形,问:有几种可能?…………………………………………( ).
(A)1种; (B)2种; (C)3种; (D)4种.
三、(本大题共有3题,每小题各6分,满分18分)
19.计算:.
20.计算:.
21.画图:已知线段a、b.
(1)画△ABC,使AB=a,BC=b,∠B=45°;
(2)画出(1)中△ABC的角平分线AD;
(3)过点D作DE⊥AB,垂足为点E,如果点D到直线AB的垂线段的长度为1.7,那么点D到直线AC的距离为 .
四、(本大题共有5题,第22、23题各6分,第24题 8分,第25题10分,满分30分)
22.如图,已知AB∥CD,说明∠ABE、∠BED、∠CDE有怎样的数量关系.
解:∠ABE+∠BED+∠CDE= °.
说理如下:
延长CD交BE的延长线于点F,
因为AB∥CD(已知),
所以∠ABE+∠F=180°( ).
因为∠BED=∠F+∠1( ),
又因为∠CDE+∠1=180°( ),
所以∠ABE+∠BED+∠CDE
=∠ABE+∠ +∠ +∠CDE
= °.
23.如图,已知AB=AE,∠B=∠E,BC=ED,F是CD中点,说明AF⊥CD的理由.
解:联结 .
在△ABC和△AED中,
HYPERLINK "http://www.21cnjy.com"
所以△ABC≌△AED ( ) ,
所以 = ( ).
所以△ACD是等腰三角形.
由F是CD的中点 ( ),
得AF⊥CD ( ) .
24.如图,在△ABC中, ( http: / / www.21cnjy.com )已知AD平分∠BAC,E是边AB上的一点,AE=AC,F是边AC上的一点,联结DE、CE、FE,当EC平分∠DEF时,猜测EF、BC的位置关系,并说明理由.
解:、的位置关系是 .
说理如下:
因为是的角平分线(已知)
所以.
在△和△中,
HYPERLINK "http://www.21cnjy.com"
所以△≌△().
得 (全等三角形的对应边相等).
(完成以下说理过程)
25.如图,等边△ABC,点P在△ABC内,点Q在△ABC外,分别联结AP、BP、AQ、CQ,∠ABP=∠ACQ,BP=CQ.
(1)说明△ABP≌△ACQ;
(2)联结PQ,说明△APQ是等边三角形;
(3)联结PC,设△CPQ是以∠PQC为顶角的等腰三角形,且∠BPC=100°,求∠APB的度数.
26.如图,在平面直角坐标系中,点A的坐标为(-2,0),点B的坐标为(0,n),以点B为直角顶点,点C在第二象限内,作等腰直角△ABC.
(1)求点C的坐标(用字母n表示)(提示:过点C作y轴的垂线)
(2)如果△ABC的面积为5.5,求n的值;
(3)在(2)的条件下,坐标平面内是否 ( http: / / www.21cnjy.com )存在一点M,使以点M、A、B为顶点组成的三角形与△ABC全等?如果存在画出符合要求的图形,并直接写出点M的坐标.
(第26题图) (第26题备用图)
普陀区2013学年度第二学期初中七年级数学期末质量调研
参考答案与评分意见2014.6
一、填空题(本大题共有14题,每题2分,满分28分)
1.; 2.; 3.; 4.<; 5.; 6.;
7. DC// AB; 8.锐角; 9.55° 10.∠A=∠D或∠DEF=∠B或;
11.66°; 12.; 13.80°或20°; 14.78°.
二、单项选择题(本大题共有4题,每题3分,满分共12分)
15.B; 16.D ; 17.A; 18.C.
三、(本大题共有3题,每小题各6分,满分18分)
19.解:原式=………………………………………(3分)
=…………………………………………………………(2分)
=.……………………………………………………………(1分)
20.解: 原式= ………………………………………………(2分)
= ………………………………………………… (2分)
= …………………………………………………………(1分)
=9. ……………………………………………………………(1分)
21.(1)画图正确2分………………………………………………………………(2分)
结论1分……………………………………………………………………(1分)
(2)画图正确……………………………………………………………………(1分)
(3)点D到直线AC的距离为1.7. …………………………………………(2分)
四、(本大题共有5题,第22、23题各6分,第24题 8分,第25题10分,满分30分)
22.解: 360°, ……………………………………………………………………(1分)
两直线平行,同旁内角互补.……………………………………………(1分)
三角形的一个外角等于与它不相邻的两个内角的和,…………………(1分)
邻补角的意义或平角意义, ……………………………………………(1分)
∠F+∠1 , …………………………………………………………………(1分)
360°.………………………………………………………………………(1分)
23.解:联结 AC、AD . …………………………………………………………(1分)
在△ABC和△AED中,
HYPERLINK "http://www.21cnjy.com"
所以△ABC≌△AED ( S.A S. ) ,……………………………………………(1分)
所以 AC = AD (全等三角形的对应边相等).…………………(1分+1分)
所以△ACD是等腰三角形 .
又因为F是CD的中点 ( 已知 ),…………………………………………(1分)
所以AF⊥CD ( 等腰三角形的三线合一 ) .………………………………(1分)
24.解:、的位置关系是 EF∥BC .……………………………(1分)
理由如下:
因为是的角平分线(已知)
所以.
在△和△中,
HYPERLINK "http://www.21cnjy.com" …………………………………………………(1分+1分)
所以△≌△().
得 DE =DC (全等三角形的对应边相等).……………………………(1分)
所以.……………………………………………………………………(1分)
因为平分(已知),
所以.……………………………………………………………………(1分)
得.………………………………………………………………………(1分)
所以EF∥BC(内错角相等,两直线平行).………………………………(1分)
( http: / / www.21cnjy.com )
25.解:(1)因为△ABC是等边三角形(已知),
所以AB=AC,∠BAC=60°(等边三角形的性质).……………… (2分)
在△和△中,
HYPERLINK "http://www.21cnjy.com"
所以△≌△(S.A.S).……………………(1分)
(2)因为△≌△,
所以,∠1=∠2(全等三角形的对应边、对应角相等).……(1分)
因为∠1+∠3=60°,
所以∠2+∠3=60°.…………………………………………………………(1分)
即.
所以△是等边三角形(有一个角是60°的等腰三角形是等边三角形).( 1分)
(3)因为△≌△,
所以(全等三角形的对应角相等).(1分)
设,
那么.
因为△是等边三角形,
所以.
得.
因为,
所以(等边对等角).……………………………………… (1分)
因为(三角形的内角和等于180o),
所以.
因为,
又因为,
所以.……………………………………… (1分)
解得.………………………………………………………………(1分)
所以为.
26.解:
(1)过点作轴的垂线CH,垂足为H,
得.
因为△是等腰直角三角形,
所以,.…(1分)
又因为,
所以.
在△和△中,
HYPERLINK "http://www.21cnjy.com"
所以△≌△().……………………………………………(1分)
所以, .
点的坐标是.……………(1分+1分)(横坐标、纵坐标各1分)
(2),………………………………(1分)
(负值已舍)………………………………………………(1分)
(3)(每个点及其坐标2分,其中点的位置1分,坐标1分)
a
b
C
B
A
C
B
A
同课章节目录
