相似图形的特征[下学期]

课件24张PPT。第五章 相似形相似形线段的比小 结全等形指能够完全重合的两个图形，即它们的形状和大小完全相同。回忆——形状相同,大小不 一定相等的图形叫做相似形。 问题:
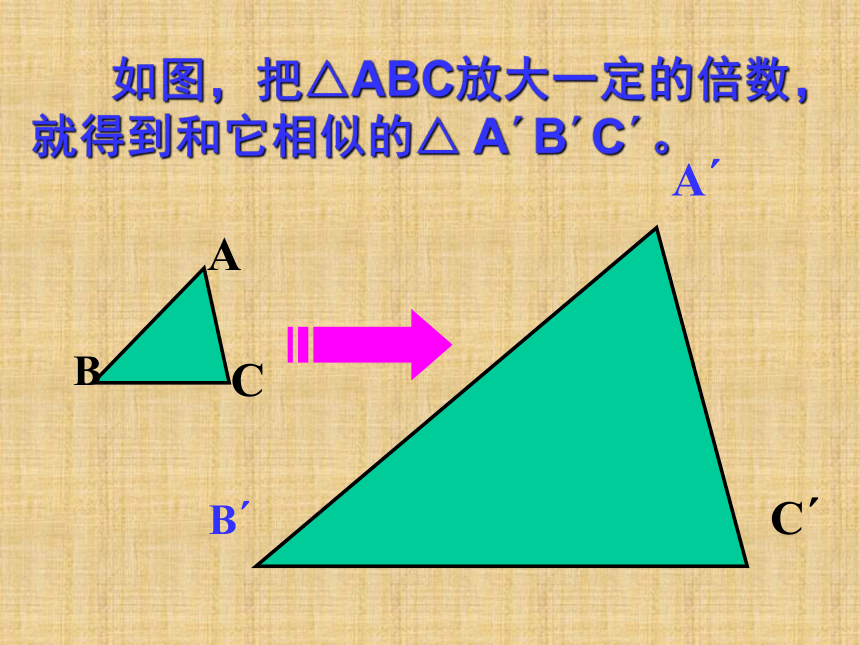
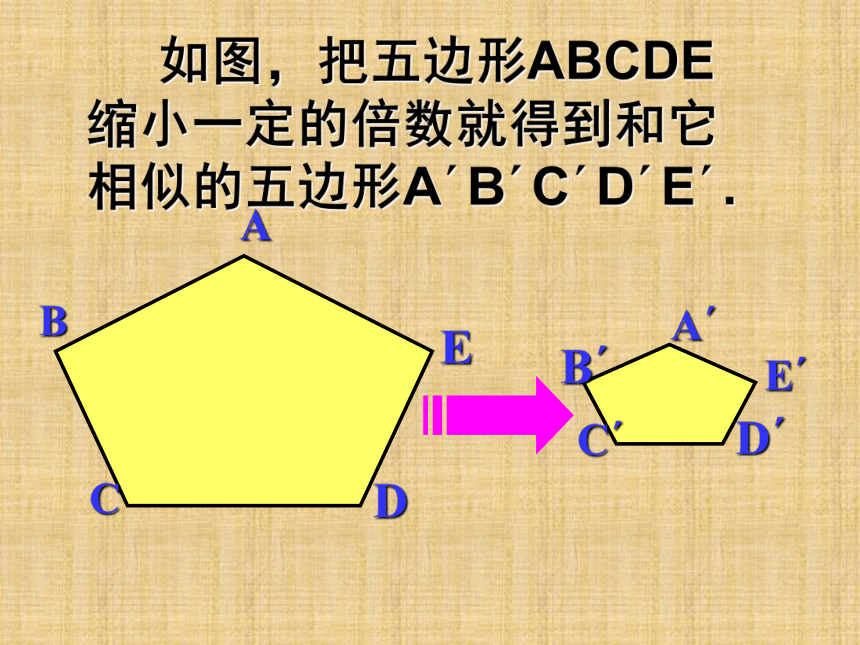
在现实生活中, 同学们还见过哪些形状相同但大小不一定相等的图形？ 如图，把△ABC放大一定的倍数， 就得到和它相似的△ A′B′C′。如图，把五边形ABCDE 缩小一定的倍数就得到和它 相似的五边形A′B′C′D′E′.两个相似图形之间 有何特征？所以研究相似图形,先要学习线段的比和比例线段的有关知识。答：两个相似多边形的对应边成比例,对应角相等.线段的比: 若选用同一长度单位量得两线段a,b 的长度分别是m,n.则两线段之比a:b=m:n或
线段 a叫做比例的前项,线段 b叫做比例的后项.（l）两条线段的比就是它们
的长度的比。 a:b=k或a=kb
说明a是b的k倍.
（2）由于线段的长度都是正数,所以线段的比K是正数。注意 （3）求两条线段的比时,要选用同一长度单位，如果给定的两条线段的长度单位不同，要先化成同一长度单位，再求它们的比。注意（4）在两条线段的比 a:b 中 ，若改变 a, b的先后顺序,(除了a=b 之外), 则 a:b 与b:a互为倒数。解： 解：解：例1:一张桌子的长a=1.25 m , 宽b=0.75m,则长与宽之比为多少? 一张桌子的长a=1.25 m , 宽b=0.75m, 则长与宽之比为多少?解： 例1:一张桌子的长a=1.25 m , 宽b=0.75m,则长与宽之比为多少? 一张桌子的长a=1.25 m , 宽b=0.75m, 则长与宽之比为多少? 上面分别采用m,cm,mm三种不同的长度单位，求得的比值相等，所以说，两条线段的比与所采用的长度单位无关，但求比时两条线段的长度单位必须一致。 例2.A,B两地的实际距离 AB=250m,画在图上的距离A′B′=5cm，求图上的距离与实际距离的比。 比例尺——
图上长度与实际长度的比。解答:取米作为共同的长度单位，
那么AB=250m A′B′=0.05m
答：图上距离与实际距离的比是
1 : 5000。∴练 习 一：教材:P69 例题3已知：在Rt△ABC中，∠C=90°，∠A=30°，斜边AB=2，求 解答：∵在Rt△ABC中,∠C=90,∠A=30°
根据勾股定理：∴ 练习2： 延长线段AB到C，使BC=AB，求：
①AC:AB；②AB:BC；③BC:ACABC解：AC:AB=2:1=2AB:BC=1:1=1BC:AC=1:2 3：已知等边三角形的边长为 a ，求高与边长之比.解答：如图 ∵ AD为等边△ABC的高
在Rt △ABD中AB=a
小结:相似形:形状相同，大小不一定
相等的图形叫做相似形。 比例尺:图上长度与实际长度的比.相似形: 形状相同,大小不一定
相等的图形叫做相似形。 线段的比:若选用同一长度单位量得两线段a,b 的长度分别是m,n.则两线段之比a:b=m:n作 业