相似图形的特征[下学期]
图片预览



文档简介
八年级数学华师大版(下册)§18.2 相似图形的特征 第一课时
一、教学目标
1.通过观察、测量让学生了解线段的比、成比例线段的概念.
2.会求线段的比,会判断已知线段是否成比例.
3.通过对图形的欣赏和分析,通过建筑、艺术上的实例了解黄金分割,培养数学美.
二、教学重难点
教学重点:对线段的比的理解及会判断成比例线段.
教学难点:掌握成比例线段的特点,欣赏生活中的数学美.
三、教学方法
多媒体教学——创设情境,以境激趣
探索教学法——调动学生主动参与探索知识、运用知识过程
四、教学用具
多媒体电教及教学软件
五、教学过程设计
1、创设情境,设疑激趣
(多媒体演示)
自然界中美丽的蝴蝶、一片树叶,生活中的蒙娜丽莎像、五角星图以及古希腊的雅典帕德嫩神庙、埃及的金字塔等都给人以最优美、最令人赏心悦目的视觉,为什么它们能令人有如此的感觉呢?
(欣赏完图片,学生讨论并引入课题)
两个相似的平面图形之间有什么关系呢?为什么有些图形是相似的,而有些
不是呢?相似图形有什么主要特征呢?
(通过多媒体的直观演示,设置问题情境,营造良好的课堂气氛,激发学生的学习兴趣。)
2、探索研究,揭示概念
线段的比和成比例线段
(1)做一做:
下图是某个城市的大小不同的两张地图,当然,它们是相似的图形。设在大地图中有A、B、C三地,在小地图中的相应三地记为A′、B′、C′,试用刻度尺量一量两张地图中AB、BC、与A′B′、B′C′的图上距离.
思考与讨论
① AB=__________cm,BC=____________cm;
A′B′=__________cm,B′C′=_____________cm
②分别计算等于多少?
(小地图是由大地图缩小得来的,我们能感到线段A′B′、B′C′与AB、BC的长度相比都“同样程度”地缩小了.)
③显然两张地图中AB和A′B′、BC和B′C′的长度都是不相等的,那么它们之间有什么关系呢?
(通过学生的交流,培养他们的合作精神和欣赏他人的意识.)
显然,我们能发现:
结论
线段的比:如果选用同一个长度单位度量两条线段AB、CD的长度,它们的长度比就是这两条线段的比.
成比例线段:对于四条线段a、b、c、d,如果其中两条线段的长度的比与另两条线段的长度的比相等,即(或a:b=c:d),那么,这四条线段叫做成比例线段,简称比例线段.
(2)议一议:
①请量一量AC= cm , A′C′= cm ,再计算你又发现什么?
②AB、BC、AC和A′B′、B′C′、A′C′中,哪四条线段分别成比例?请分别写它们的比例式.
③如果在这两张地图中,你猜猜会出现什么情况
④如果在测量时,AB的长度单位采用厘米而A′B′的长度单位采用分米,那么它们的比有没有变化
⑤两条线段长度的比与所采用的长度单位有没有关系
(3)说一说:请举出生活中利用线段比的事例.如:按比例绘制地图等.
(通过相关练习,巩固概念.)
知识的迁移
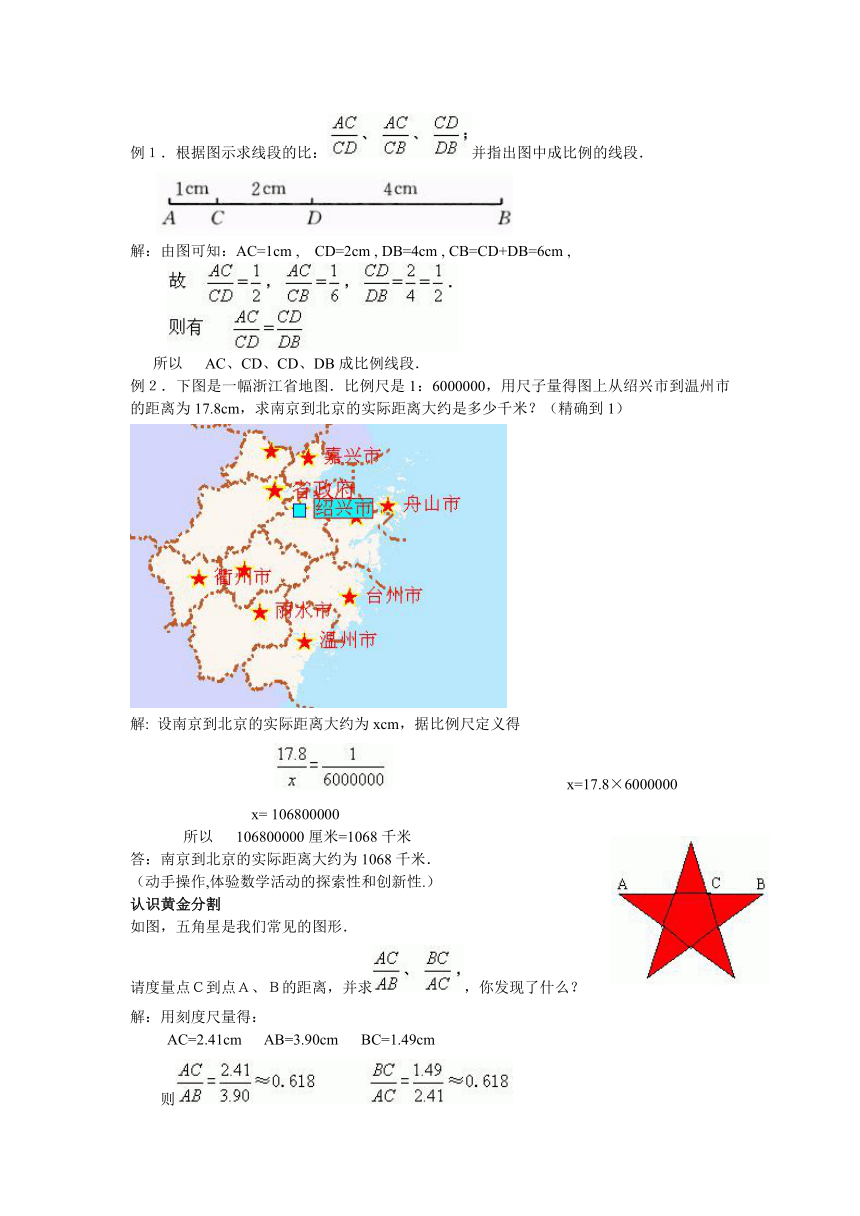
例1.根据图示求线段的比:并指出图中成比例的线段.
解:由图可知:AC=1cm , CD=2cm , DB=4cm , CB=CD+DB=6cm ,
所以 AC、CD、CD、DB成比例线段.
例2.下图是一幅浙江省地图.比例尺是1:6000000,用尺子量得图上从绍兴市到温州市的距离为17.8cm,求南京到北京的实际距离大约是多少千米?(精确到1)
解: 设南京到北京的实际距离大约为xcm,据比例尺定义得
x=17.8×6000000
x= 106800000
所以 106800000厘米=1068千米
答:南京到北京的实际距离大约为1068千米.
(动手操作,体验数学活动的探索性和创新性.)
认识黄金分割
如图,五角星是我们常见的图形.
请度量点C到点A、B的距离,并求,你发现了什么?
解:用刻度尺量得:
AC=2.41cm AB=3.90cm BC=1.49cm
则
故即线段AB、AC、AC、BC成比例线段.
如图,点C把线段AB分成两条线段AC和BC,如果,那么称线段AB被点C黄金分割,点C叫做线段AB的黄金分割点.
自古希腊以来,人们认为黄金分割点是分割线段时最优美的、最令人赏心悦目的点,黄金分割也就被视为最美丽的几何学比率.而古希腊的雅典帕德嫩神庙、埃及的金字塔、生活中的蒙娜丽莎像、五角星图以及自然界美丽的蝴蝶、一片树叶等物体中都充满了黄金分割,故给人以优美、赏心悦目的感觉.
(通过知识的直接运用及训练巩固,使知识融会贯通。)
3、反馈练习,思维拓展
(1)基础练习:
①如图,☆与 △ 的个数比为 .
②一条线段的长度是另一条线段长度的3倍,则这两条线段的比是
.
③等腰三角形两腰的比是 ,直角三角形斜边上的中线与斜边的比是 .
④如果线段a、b、c、d成比例,且b=3cm,c=2cm,d=6cm则线段a= .
⑤A、B两地的实际距离为250m,画在图上的距离A′B′为5 cm,则图上距离与实际距离的比是 .
(2)提高练习:
在比例尺为1:8000的某学校地图上,矩形运动场的图上尺寸是1cm2cm,矩形运动场的实际尺寸是多少
(3)思维拓展:
画家一般是这样画一幅壁画的:开始先画一个小的画,然后把一个正方形的网格放在上面,再把要画壁画的地方分成一个大的网格,最后一个方格一个方格地把原图画到对应的大的网格的对应位置上.请你根据这个过程,放大左边的图案.
(通过知识的综合应用,拓宽学生的视野,提高他们灵活运用知识的能力,培养学生的发散思维。)
4、回顾反思,整体评价
今天我们认识了线段的比,如何求线段的比?成比例线段有什么特征?
(让学生总结,通过问题的回答,引导学生自主总结,把分散的知识系统化、结构化,形成知识网络,完善学生的认知结构,加深对所学知识的理解.)
5、课外作业与拓展
① P70 1、2、3、4.
② 思考:如何利用影长测量学校旗杆的高度?(提示:相同时刻物高与影长成比例)
③ 课外拓展:《课时导航》华师大版八年级(下)P33-P34
第二课时
一、教学目标
1.经历自主探索相似图形的特征的过程,理解相似多边形对应角相等、对应边成比例以及面积比的关系.
2.通过实践,掌握利用相似图形的特征计算边的长度或角的度数.
3.培养学生“观察-猜想-验证-实践”的研究问题的思维方式.
二、教学重难点
教学重点:探索并掌握相似图形的特征.
教学难点:探索与研究问题的思维方式.
三、教学方法
多媒体教学——创设情境,以境激趣
探索教学法——调动学生主动参与探索知识、运用知识过程
四、教学用具
多媒体电教及教学软件
五、教学过程设计
1、创设情境,设疑激趣
(多媒体演示)
当你走进学校,仰头望着操场旗杆上高高飘扬的五星红旗时,你也许很想知道,操场上的旗杆到底有多高呢?
通常一种简便的方法是:如下图所示,站在操场上,请你的同学量出你在太阳下的影子长度OC、旗杆的影子长度OA,再量出你的身高CD,根据三角形OCD与三角形OAB相似,就可以计算出旗杆的高度AB了.
如果测得OC= 0.8米,OA=5米,CD=1.6米,如何求AB的高呢
下面我们一起来研究、解决这个问题.
(通过多媒体的直观演示,设置问题情境,营造良好的课堂气氛,激发学生的学习兴趣。)
2、探索研究,揭示特征
相似图形的特征
(1)提出猜想:
上节课我们研究了P67两张相似地图中的对应线段AB与A′B′、BC与B′C′、AC与A′C′的比相等,即
请你由此猜想两张相似地图中的对应线段有什么关系?
――显然,两张相似地图中的对应线段都是成比例的.
这个结论对一般的相似多边形是否成立呢?我们不妨通过下面测量与计算来说明.
(2)进行验证:
仔细观察下面两幅图形,量一量、算一算它们的对应边之间是否有以上的关系?对应角之间又有什么关系呢?
通过测量与计算,我们可得:
图(一)中:
且 ∠A=∠A′ ∠B=∠B′∠C=∠C′∠D=∠D′
图(二)中:
且 ∠A=∠A′ ∠B=∠B′∠C=∠C′∠D=∠D′∠E=∠E′
即:相似四边形、相似五边形的对应边各成比例,对应角各相等.
思考与讨论
①由此可知两个相似多边形的特征是什么?
(对应边成比例,对应角相等.)
②由相似多边形的特征可否得到识别两个多边形是否相似的方法?举例说明.
(如果两个多边形的对应边成比例且对应角相等,那么这两个多边形相似.)
实践运用
议一议 观察下面两组图形,各组图形是否相似?为什么?与同伴交流.
(通过学生的交流,培养他们的合作精神和欣赏他人的意识.)
思考: 如果两个多边形不相似,那么它们的对应角有可能都相等吗 对应边有可能都成比例吗
做一做 一块长3m、宽1.5m的矩形黑板如图所示,镶在其外围的木质边框宽7.5m.边框的内外边缘所成的矩形相似吗 为什么
(动手操作,体验数学活动的探索性和创新性.)
算一算: (1)测量旗杆的问题:如图,三角形OCD与三角形OAB相似,由相似多边形的特征可得:
即: AB=10(米)
答:旗杆的高度AB为10米.
(2)P69例1.在下图所示的相似四边形中求未知边x、y的长度和角度a的大小.
分析:由相似多边形的特征可得:,则可分别求出x、y.再由相似多边形的对应角相等及四边形的内角和为360 ,即可求出角度的大小.
(让学生板书,并参阅P69)
解:(略)(通过知识的直接运用及训练巩固,使知识融会贯通。)
3、知识迁移,拓展思维
基础练习:P70 3、4、5.
思维拓展:
(1)讨论:①两个三角形一定是相似形吗?两个等腰三角形呢?两个等边三角形呢?
②所有的矩形都相似吗?所有的正方形呢?
(2)思考:工人师傅按照比例尺为1:2的图纸制作三角形零件.如图所示,该零件的横截面为△ABC,画在图纸上是△DEF,CH、FG分别是它们的高。
①找出图中的相似三角形,并简述理由.
②CH与FG的比是多少?
③你发现了什么?与同伴交流。
(通过知识的综合应用,拓宽学生的视野,提高他们灵活运用知识的能力,培养学生的发散思维。)
4、回顾反思,整体评价
今天我们掌握了相似多边形的特征,如何利用这个特征求线段的长度?又如何判别两个多边形相似呢?(让学生总结,通过问题的回答,引导学生自主总结,把分散的知识系统化、结构化,形成知识网络,完善学生的认知结构,加深对所学知识的理解.)
5、课外实践,布置作业
① P70 习题18.2 5、6
②思考:如图,BC与EF在一条直线上,AC∥DF.将图(2)的三角形截去一块,使它变为与图(1)相似的图形.如何截法?与同伴交流.
一、教学目标
1.通过观察、测量让学生了解线段的比、成比例线段的概念.
2.会求线段的比,会判断已知线段是否成比例.
3.通过对图形的欣赏和分析,通过建筑、艺术上的实例了解黄金分割,培养数学美.
二、教学重难点
教学重点:对线段的比的理解及会判断成比例线段.
教学难点:掌握成比例线段的特点,欣赏生活中的数学美.
三、教学方法
多媒体教学——创设情境,以境激趣
探索教学法——调动学生主动参与探索知识、运用知识过程
四、教学用具
多媒体电教及教学软件
五、教学过程设计
1、创设情境,设疑激趣
(多媒体演示)
自然界中美丽的蝴蝶、一片树叶,生活中的蒙娜丽莎像、五角星图以及古希腊的雅典帕德嫩神庙、埃及的金字塔等都给人以最优美、最令人赏心悦目的视觉,为什么它们能令人有如此的感觉呢?
(欣赏完图片,学生讨论并引入课题)
两个相似的平面图形之间有什么关系呢?为什么有些图形是相似的,而有些
不是呢?相似图形有什么主要特征呢?
(通过多媒体的直观演示,设置问题情境,营造良好的课堂气氛,激发学生的学习兴趣。)
2、探索研究,揭示概念
线段的比和成比例线段
(1)做一做:
下图是某个城市的大小不同的两张地图,当然,它们是相似的图形。设在大地图中有A、B、C三地,在小地图中的相应三地记为A′、B′、C′,试用刻度尺量一量两张地图中AB、BC、与A′B′、B′C′的图上距离.
思考与讨论
① AB=__________cm,BC=____________cm;
A′B′=__________cm,B′C′=_____________cm
②分别计算等于多少?
(小地图是由大地图缩小得来的,我们能感到线段A′B′、B′C′与AB、BC的长度相比都“同样程度”地缩小了.)
③显然两张地图中AB和A′B′、BC和B′C′的长度都是不相等的,那么它们之间有什么关系呢?
(通过学生的交流,培养他们的合作精神和欣赏他人的意识.)
显然,我们能发现:
结论
线段的比:如果选用同一个长度单位度量两条线段AB、CD的长度,它们的长度比就是这两条线段的比.
成比例线段:对于四条线段a、b、c、d,如果其中两条线段的长度的比与另两条线段的长度的比相等,即(或a:b=c:d),那么,这四条线段叫做成比例线段,简称比例线段.
(2)议一议:
①请量一量AC= cm , A′C′= cm ,再计算你又发现什么?
②AB、BC、AC和A′B′、B′C′、A′C′中,哪四条线段分别成比例?请分别写它们的比例式.
③如果在这两张地图中,你猜猜会出现什么情况
④如果在测量时,AB的长度单位采用厘米而A′B′的长度单位采用分米,那么它们的比有没有变化
⑤两条线段长度的比与所采用的长度单位有没有关系
(3)说一说:请举出生活中利用线段比的事例.如:按比例绘制地图等.
(通过相关练习,巩固概念.)
知识的迁移
例1.根据图示求线段的比:并指出图中成比例的线段.
解:由图可知:AC=1cm , CD=2cm , DB=4cm , CB=CD+DB=6cm ,
所以 AC、CD、CD、DB成比例线段.
例2.下图是一幅浙江省地图.比例尺是1:6000000,用尺子量得图上从绍兴市到温州市的距离为17.8cm,求南京到北京的实际距离大约是多少千米?(精确到1)
解: 设南京到北京的实际距离大约为xcm,据比例尺定义得
x=17.8×6000000
x= 106800000
所以 106800000厘米=1068千米
答:南京到北京的实际距离大约为1068千米.
(动手操作,体验数学活动的探索性和创新性.)
认识黄金分割
如图,五角星是我们常见的图形.
请度量点C到点A、B的距离,并求,你发现了什么?
解:用刻度尺量得:
AC=2.41cm AB=3.90cm BC=1.49cm
则
故即线段AB、AC、AC、BC成比例线段.
如图,点C把线段AB分成两条线段AC和BC,如果,那么称线段AB被点C黄金分割,点C叫做线段AB的黄金分割点.
自古希腊以来,人们认为黄金分割点是分割线段时最优美的、最令人赏心悦目的点,黄金分割也就被视为最美丽的几何学比率.而古希腊的雅典帕德嫩神庙、埃及的金字塔、生活中的蒙娜丽莎像、五角星图以及自然界美丽的蝴蝶、一片树叶等物体中都充满了黄金分割,故给人以优美、赏心悦目的感觉.
(通过知识的直接运用及训练巩固,使知识融会贯通。)
3、反馈练习,思维拓展
(1)基础练习:
①如图,☆与 △ 的个数比为 .
②一条线段的长度是另一条线段长度的3倍,则这两条线段的比是
.
③等腰三角形两腰的比是 ,直角三角形斜边上的中线与斜边的比是 .
④如果线段a、b、c、d成比例,且b=3cm,c=2cm,d=6cm则线段a= .
⑤A、B两地的实际距离为250m,画在图上的距离A′B′为5 cm,则图上距离与实际距离的比是 .
(2)提高练习:
在比例尺为1:8000的某学校地图上,矩形运动场的图上尺寸是1cm2cm,矩形运动场的实际尺寸是多少
(3)思维拓展:
画家一般是这样画一幅壁画的:开始先画一个小的画,然后把一个正方形的网格放在上面,再把要画壁画的地方分成一个大的网格,最后一个方格一个方格地把原图画到对应的大的网格的对应位置上.请你根据这个过程,放大左边的图案.
(通过知识的综合应用,拓宽学生的视野,提高他们灵活运用知识的能力,培养学生的发散思维。)
4、回顾反思,整体评价
今天我们认识了线段的比,如何求线段的比?成比例线段有什么特征?
(让学生总结,通过问题的回答,引导学生自主总结,把分散的知识系统化、结构化,形成知识网络,完善学生的认知结构,加深对所学知识的理解.)
5、课外作业与拓展
① P70 1、2、3、4.
② 思考:如何利用影长测量学校旗杆的高度?(提示:相同时刻物高与影长成比例)
③ 课外拓展:《课时导航》华师大版八年级(下)P33-P34
第二课时
一、教学目标
1.经历自主探索相似图形的特征的过程,理解相似多边形对应角相等、对应边成比例以及面积比的关系.
2.通过实践,掌握利用相似图形的特征计算边的长度或角的度数.
3.培养学生“观察-猜想-验证-实践”的研究问题的思维方式.
二、教学重难点
教学重点:探索并掌握相似图形的特征.
教学难点:探索与研究问题的思维方式.
三、教学方法
多媒体教学——创设情境,以境激趣
探索教学法——调动学生主动参与探索知识、运用知识过程
四、教学用具
多媒体电教及教学软件
五、教学过程设计
1、创设情境,设疑激趣
(多媒体演示)
当你走进学校,仰头望着操场旗杆上高高飘扬的五星红旗时,你也许很想知道,操场上的旗杆到底有多高呢?
通常一种简便的方法是:如下图所示,站在操场上,请你的同学量出你在太阳下的影子长度OC、旗杆的影子长度OA,再量出你的身高CD,根据三角形OCD与三角形OAB相似,就可以计算出旗杆的高度AB了.
如果测得OC= 0.8米,OA=5米,CD=1.6米,如何求AB的高呢
下面我们一起来研究、解决这个问题.
(通过多媒体的直观演示,设置问题情境,营造良好的课堂气氛,激发学生的学习兴趣。)
2、探索研究,揭示特征
相似图形的特征
(1)提出猜想:
上节课我们研究了P67两张相似地图中的对应线段AB与A′B′、BC与B′C′、AC与A′C′的比相等,即
请你由此猜想两张相似地图中的对应线段有什么关系?
――显然,两张相似地图中的对应线段都是成比例的.
这个结论对一般的相似多边形是否成立呢?我们不妨通过下面测量与计算来说明.
(2)进行验证:
仔细观察下面两幅图形,量一量、算一算它们的对应边之间是否有以上的关系?对应角之间又有什么关系呢?
通过测量与计算,我们可得:
图(一)中:
且 ∠A=∠A′ ∠B=∠B′∠C=∠C′∠D=∠D′
图(二)中:
且 ∠A=∠A′ ∠B=∠B′∠C=∠C′∠D=∠D′∠E=∠E′
即:相似四边形、相似五边形的对应边各成比例,对应角各相等.
思考与讨论
①由此可知两个相似多边形的特征是什么?
(对应边成比例,对应角相等.)
②由相似多边形的特征可否得到识别两个多边形是否相似的方法?举例说明.
(如果两个多边形的对应边成比例且对应角相等,那么这两个多边形相似.)
实践运用
议一议 观察下面两组图形,各组图形是否相似?为什么?与同伴交流.
(通过学生的交流,培养他们的合作精神和欣赏他人的意识.)
思考: 如果两个多边形不相似,那么它们的对应角有可能都相等吗 对应边有可能都成比例吗
做一做 一块长3m、宽1.5m的矩形黑板如图所示,镶在其外围的木质边框宽7.5m.边框的内外边缘所成的矩形相似吗 为什么
(动手操作,体验数学活动的探索性和创新性.)
算一算: (1)测量旗杆的问题:如图,三角形OCD与三角形OAB相似,由相似多边形的特征可得:
即: AB=10(米)
答:旗杆的高度AB为10米.
(2)P69例1.在下图所示的相似四边形中求未知边x、y的长度和角度a的大小.
分析:由相似多边形的特征可得:,则可分别求出x、y.再由相似多边形的对应角相等及四边形的内角和为360 ,即可求出角度的大小.
(让学生板书,并参阅P69)
解:(略)(通过知识的直接运用及训练巩固,使知识融会贯通。)
3、知识迁移,拓展思维
基础练习:P70 3、4、5.
思维拓展:
(1)讨论:①两个三角形一定是相似形吗?两个等腰三角形呢?两个等边三角形呢?
②所有的矩形都相似吗?所有的正方形呢?
(2)思考:工人师傅按照比例尺为1:2的图纸制作三角形零件.如图所示,该零件的横截面为△ABC,画在图纸上是△DEF,CH、FG分别是它们的高。
①找出图中的相似三角形,并简述理由.
②CH与FG的比是多少?
③你发现了什么?与同伴交流。
(通过知识的综合应用,拓宽学生的视野,提高他们灵活运用知识的能力,培养学生的发散思维。)
4、回顾反思,整体评价
今天我们掌握了相似多边形的特征,如何利用这个特征求线段的长度?又如何判别两个多边形相似呢?(让学生总结,通过问题的回答,引导学生自主总结,把分散的知识系统化、结构化,形成知识网络,完善学生的认知结构,加深对所学知识的理解.)
5、课外实践,布置作业
① P70 习题18.2 5、6
②思考:如图,BC与EF在一条直线上,AC∥DF.将图(2)的三角形截去一块,使它变为与图(1)相似的图形.如何截法?与同伴交流.
