相似三角形的识别1[下学期]
图片预览



文档简介
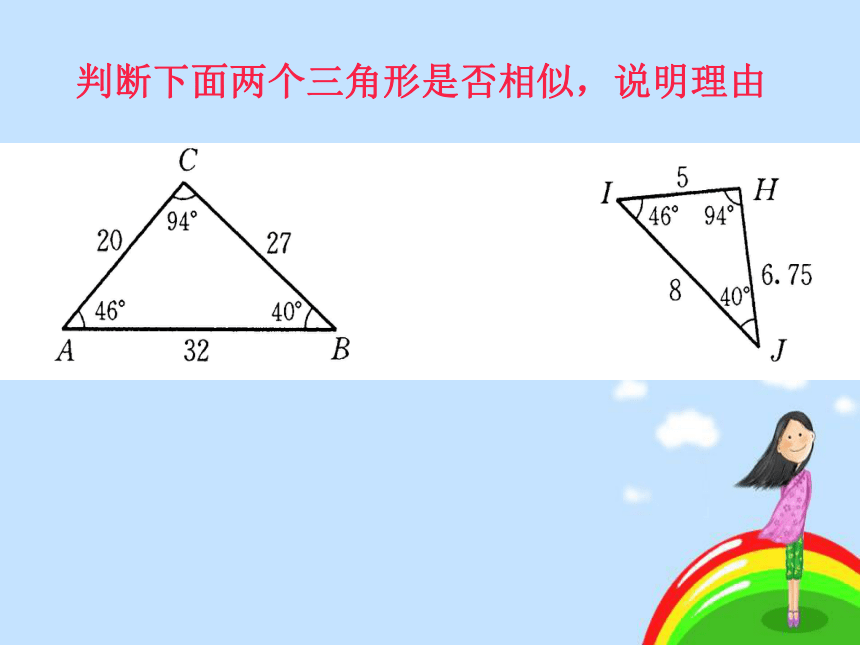
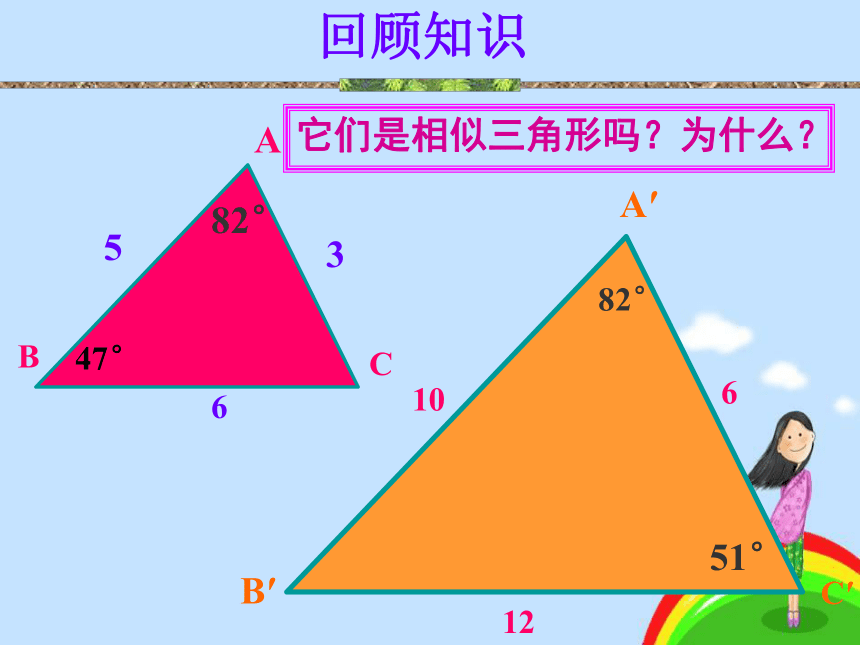
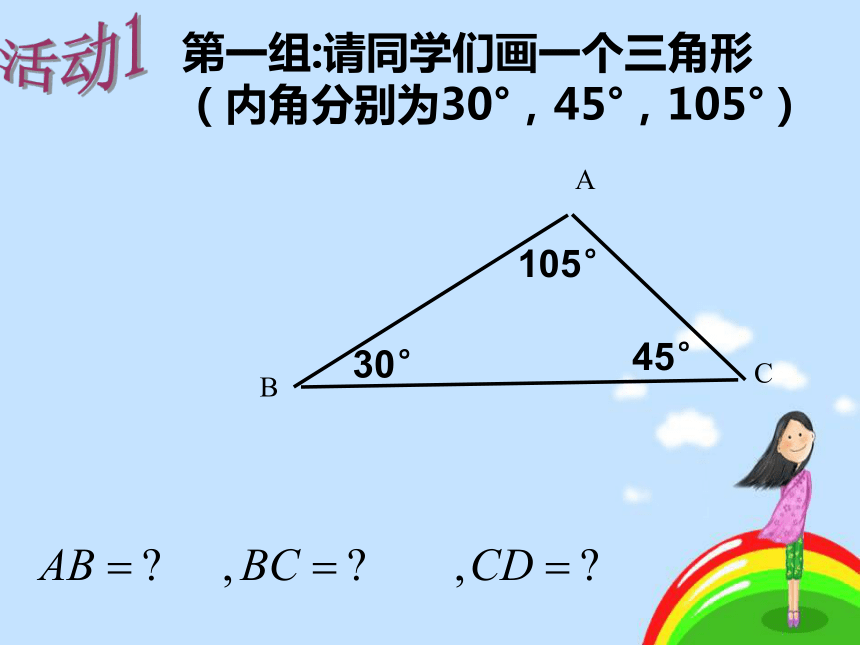
课件28张PPT。§ 18.3 相似三角形的识别(一)∠A=∠A1 、∠ B=∠B1 、∠ C=∠C1△ABC∽△A1B1C1边对应成比例,角对应相等的两个三角形相似。判断下面两个三角形是否相似,说明理由 我们现在识别两个三角形是否相似,必须要知道它们的对应角是否相等,对应边是否成比例.那么是否存在识别两个三角形相似的简便方法呢?第一组:请同学们画一个三角形
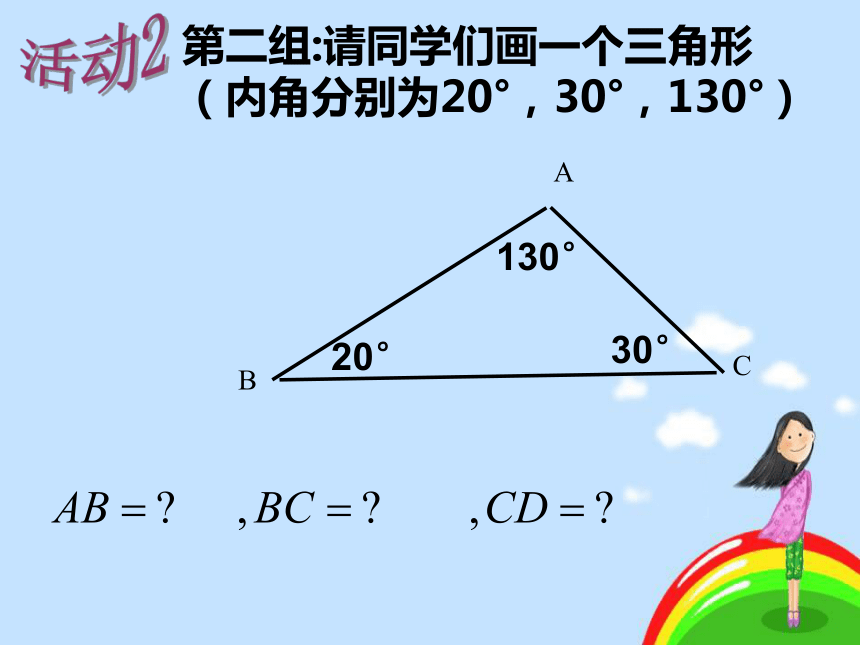
(内角分别为30°,45°,105°)活动1第二组:请同学们画一个三角形
(内角分别为20°,30°,130°)活动2第三组:请同学们画一个三角形
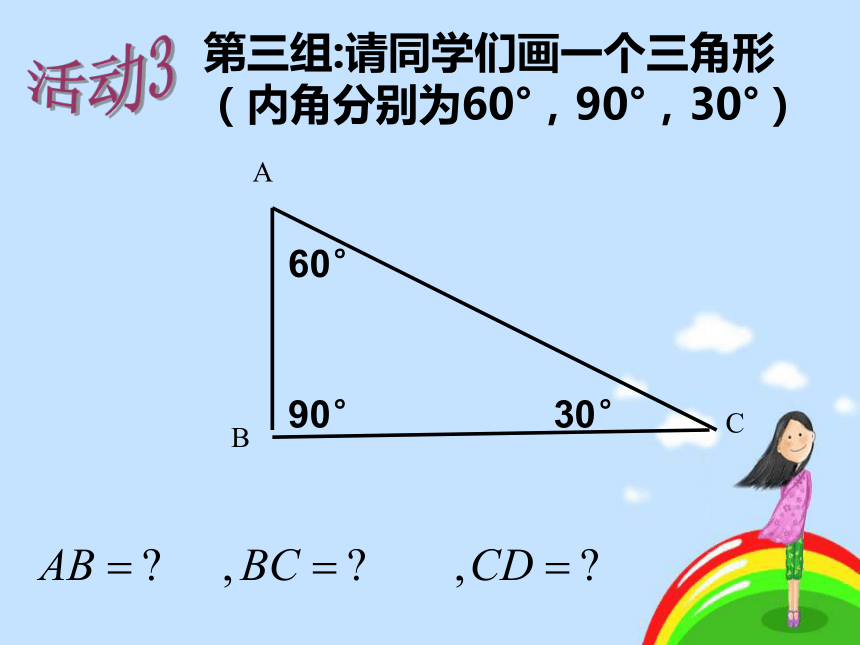
(内角分别为60°,90°,30°)活动3第四组:请同学们画一个三角形
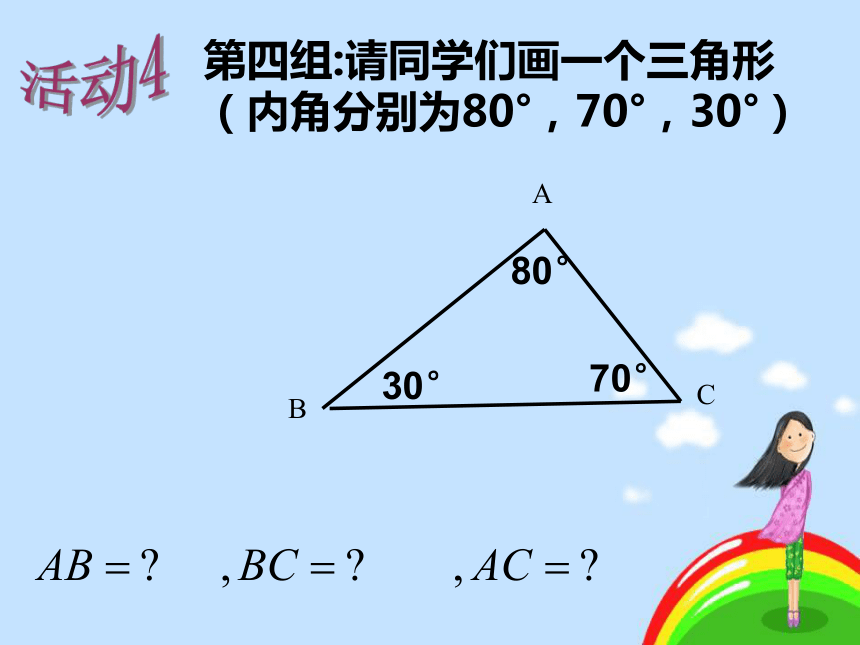
(内角分别为80°,70°,30°)活动4CC'∵ ∠A=∠A', ∠B=∠B'∴ ΔABC ∽ ΔA'B'C'用数学符号表示:相似三角形的识别(1)(1)ΔABC和ΔDEF中,
∠A=400,∠B=800,
∠E=800, ∠F=400。
ΔABC与ΔFED 。 练习1相似(填: “相似”或“不相似”, 并说明理由)。 (2)ΔABC和ΔDEF中,
∠A=400,∠B=800,
∠E=800, ∠F=600。
ΔABC与ΔDEF 。 相似如图18.3.4所示,在两个直角三角形△ABC和△A′B′C′中,
∠B=∠B′=90°,∠A=∠A′,
判断这两个三角形是否相似. 解:∵ ∠B=∠B′=90°(已知),
∠A=∠A′(已知),
∴ △ABC∽△A′B′C′(如果一个三角形的两角分别与另一个三角形
的两角对应相等,那么这两个三角形相似.) 根据给出的条件,按相应顺序写出 相似三角形并说明理由(要求步步有依据)△ ∽ △ . (1)∠1=∠2 (2)∠1=∠2△ ∽ △ . ABC ADEACB ADE△ ∽ △ . (3)∠1=∠B (4)∠1=∠2
∠E=∠C△ ∽ △ . ABC ADEABC ACDAEDCB(6) DE∥BC
△ ∽ △_____ △ ∽ △_____ (5)DE∥BC ADE ABCADE ACB相似三角形的基本图形的归纳: 例2 如图,△ABC中,
DE∥BC,EF∥AB,
试说明△ADE∽△EFC. 解:
∵DE∥BC (已知),EF∥AB(已知),
∴ ∠ADE=∠B, ∠B =∠EFC (两直线平行 ,
∠AED=∠C. 同位角相等)
∴ △ADE∽△EFC.
((如果一个三角形的两角分别与另一个三角形的
两角对应相等,那么这两个三角形相似.) ))))) 如图,△ABC中DE∥BC,GF∥AB,DE、GF交于点O,则图中与△ABC相似的三角形共有多少个?请你写出来.解: 与△ABC相似的三角形有3个:
△ADE △GFC △GOE2、图中DG∥EH∥FI∥BC,
找出图中所有的相似三角形 △ ABC∽ △ AFI∽ △ AEH ∽△ ADG3、已知:如图(7),?ABC中,CD是斜边上的高.
试说明:?ABC∽?CBD∽?ACD.
证明:∵∠B=∠B,
∠CDB=∠ACB=90°
∴?ABC∽?CBD
(两角对应相等,两三角形相似)
同理 ?ABC∽?ACD
∴?ABC∽?CBD∽?ACD结论:直角三角形被斜边上的高线分成的两个直角三角形和原三角形相似.如图,△ABC中,点D是AB上一点,且∠1=∠B。 2) 说明 : AC2=AD·AB
1) 说明: ∴△ABC~△ACD解: ∵∠A=∠A,∠B=∠1
∴△ABC~△ACD解: 由1)知: △ABC~△ACD
∴ AB:AC=AC:AD.
则 AC2=AD·AB 3) 若:AD=16, DB=9. 求AC的长.解: 由2知:
AC2=AD·AB=16(16+9)=16×25
所以 AC=20. (1)两个顶角相等的等腰三角形是相似的三角形。 ( )
(2)两个等腰直角三角形是相似三角形。 ( )
(3)底角相等的两个等腰三角形是相似三角形。 ( )
(4)两个等腰三角形只要有一个角对应相等就相似. ( )
(5)两个直角三角形一定是相似三角形。 ( )
(6)有一个角相等的两个直角三角形是相似三角形。 ( )
(7)有一个锐角相等的两个直角三角形是相似三角形。 ( )
(8)所有的正三角形都相似。 ( )
(9)一个钝角三角形和一个锐角三角形有可能相似。 ( )2、判断下列各题的对错,并说明原因;××××1.如图(1),AE与BD相交于点C,要△ABC∽△DEC,需要条件 ;
2.已知,如图(2)要△ABC∽△ACD,
需要条件 ;
3.已知,如图(3)要使△ABE∽△ACD,
需要条件 ;
图1图2图3 试着用课本第157页的格点画两个三角形。
要求: (用铅笔)有2组内角分别对应相等.(如下图)观察 (或测量计算):
这2个三角形的对应边的比值是否相同1243∠1=∠2
∠3=∠4(3)(4)(5)(6)我练,我进步 如图,△ABC中,点D是AB上一点. 解:图中的相似三角形有:
⊿ABC与⊿ACD其理由:∵∠A=∠A,∠B=∠1
∴△ABC~△ACD(1)若∠1=∠B。
写出图中的相似三角形.我练,我进步 (2) 如图,若有∠1= ∠B= ∠2,
写出图中的相似三角形.解:图中的相似三角形有:
⊿ABC∽⊿ACD∽⊿ADE(3) 如图,若有∠C= ∠2,写出图中的相似三角形.解:图中的相似三角形有:⊿ABC∽⊿AED
(内角分别为30°,45°,105°)活动1第二组:请同学们画一个三角形
(内角分别为20°,30°,130°)活动2第三组:请同学们画一个三角形
(内角分别为60°,90°,30°)活动3第四组:请同学们画一个三角形
(内角分别为80°,70°,30°)活动4CC'∵ ∠A=∠A', ∠B=∠B'∴ ΔABC ∽ ΔA'B'C'用数学符号表示:相似三角形的识别(1)(1)ΔABC和ΔDEF中,
∠A=400,∠B=800,
∠E=800, ∠F=400。
ΔABC与ΔFED 。 练习1相似(填: “相似”或“不相似”, 并说明理由)。 (2)ΔABC和ΔDEF中,
∠A=400,∠B=800,
∠E=800, ∠F=600。
ΔABC与ΔDEF 。 相似如图18.3.4所示,在两个直角三角形△ABC和△A′B′C′中,
∠B=∠B′=90°,∠A=∠A′,
判断这两个三角形是否相似. 解:∵ ∠B=∠B′=90°(已知),
∠A=∠A′(已知),
∴ △ABC∽△A′B′C′(如果一个三角形的两角分别与另一个三角形
的两角对应相等,那么这两个三角形相似.) 根据给出的条件,按相应顺序写出 相似三角形并说明理由(要求步步有依据)△ ∽ △ . (1)∠1=∠2 (2)∠1=∠2△ ∽ △ . ABC ADEACB ADE△ ∽ △ . (3)∠1=∠B (4)∠1=∠2
∠E=∠C△ ∽ △ . ABC ADEABC ACDAEDCB(6) DE∥BC
△ ∽ △_____ △ ∽ △_____ (5)DE∥BC ADE ABCADE ACB相似三角形的基本图形的归纳: 例2 如图,△ABC中,
DE∥BC,EF∥AB,
试说明△ADE∽△EFC. 解:
∵DE∥BC (已知),EF∥AB(已知),
∴ ∠ADE=∠B, ∠B =∠EFC (两直线平行 ,
∠AED=∠C. 同位角相等)
∴ △ADE∽△EFC.
((如果一个三角形的两角分别与另一个三角形的
两角对应相等,那么这两个三角形相似.) ))))) 如图,△ABC中DE∥BC,GF∥AB,DE、GF交于点O,则图中与△ABC相似的三角形共有多少个?请你写出来.解: 与△ABC相似的三角形有3个:
△ADE △GFC △GOE2、图中DG∥EH∥FI∥BC,
找出图中所有的相似三角形 △ ABC∽ △ AFI∽ △ AEH ∽△ ADG3、已知:如图(7),?ABC中,CD是斜边上的高.
试说明:?ABC∽?CBD∽?ACD.
证明:∵∠B=∠B,
∠CDB=∠ACB=90°
∴?ABC∽?CBD
(两角对应相等,两三角形相似)
同理 ?ABC∽?ACD
∴?ABC∽?CBD∽?ACD结论:直角三角形被斜边上的高线分成的两个直角三角形和原三角形相似.如图,△ABC中,点D是AB上一点,且∠1=∠B。 2) 说明 : AC2=AD·AB
1) 说明: ∴△ABC~△ACD解: ∵∠A=∠A,∠B=∠1
∴△ABC~△ACD解: 由1)知: △ABC~△ACD
∴ AB:AC=AC:AD.
则 AC2=AD·AB 3) 若:AD=16, DB=9. 求AC的长.解: 由2知:
AC2=AD·AB=16(16+9)=16×25
所以 AC=20. (1)两个顶角相等的等腰三角形是相似的三角形。 ( )
(2)两个等腰直角三角形是相似三角形。 ( )
(3)底角相等的两个等腰三角形是相似三角形。 ( )
(4)两个等腰三角形只要有一个角对应相等就相似. ( )
(5)两个直角三角形一定是相似三角形。 ( )
(6)有一个角相等的两个直角三角形是相似三角形。 ( )
(7)有一个锐角相等的两个直角三角形是相似三角形。 ( )
(8)所有的正三角形都相似。 ( )
(9)一个钝角三角形和一个锐角三角形有可能相似。 ( )2、判断下列各题的对错,并说明原因;××××1.如图(1),AE与BD相交于点C,要△ABC∽△DEC,需要条件 ;
2.已知,如图(2)要△ABC∽△ACD,
需要条件 ;
3.已知,如图(3)要使△ABE∽△ACD,
需要条件 ;
图1图2图3 试着用课本第157页的格点画两个三角形。
要求: (用铅笔)有2组内角分别对应相等.(如下图)观察 (或测量计算):
这2个三角形的对应边的比值是否相同1243∠1=∠2
∠3=∠4(3)(4)(5)(6)我练,我进步 如图,△ABC中,点D是AB上一点. 解:图中的相似三角形有:
⊿ABC与⊿ACD其理由:∵∠A=∠A,∠B=∠1
∴△ABC~△ACD(1)若∠1=∠B。
写出图中的相似三角形.我练,我进步 (2) 如图,若有∠1= ∠B= ∠2,
写出图中的相似三角形.解:图中的相似三角形有:
⊿ABC∽⊿ACD∽⊿ADE(3) 如图,若有∠C= ∠2,写出图中的相似三角形.解:图中的相似三角形有:⊿ABC∽⊿AED
