华东师大版九年级数学上册 第二十三章图形的相似单元测试卷 (含答案)
文档属性
| 名称 | 华东师大版九年级数学上册 第二十三章图形的相似单元测试卷 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1017.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-05 21:20:07 | ||
图片预览



文档简介
图形的相似单元测试卷
姓名____________ 时间:90分钟 满分:120分 总分_________
注意事项:
1. 请在试卷规定时间内作答.
2. 请注意答题规范,书写规范.
3. 请用0.5毫米黑色水笔把答案直接答在试卷上.
一、选择题(每小题3分,共30分)
1. 已知,则下列比例式成立的是 【 】
(A) (B) (C) (D)
2. 如图所示,在△ABC中,,则AC的长为 【 】
(A)6 (B)7 (C)8 (D)9
3. 如图所示,在△ABC中,点D、E分别在边AB、AC上,DE与BC不平行,添加下列条件仍不能判定△ADE∽△ACB的是 【 】
(A) (B)
(C) (D)
4. 如图所示,△ABC的中线BE、CF交于点O,
连结EF,则的值为 【 】
(A) (B) (C) (D)
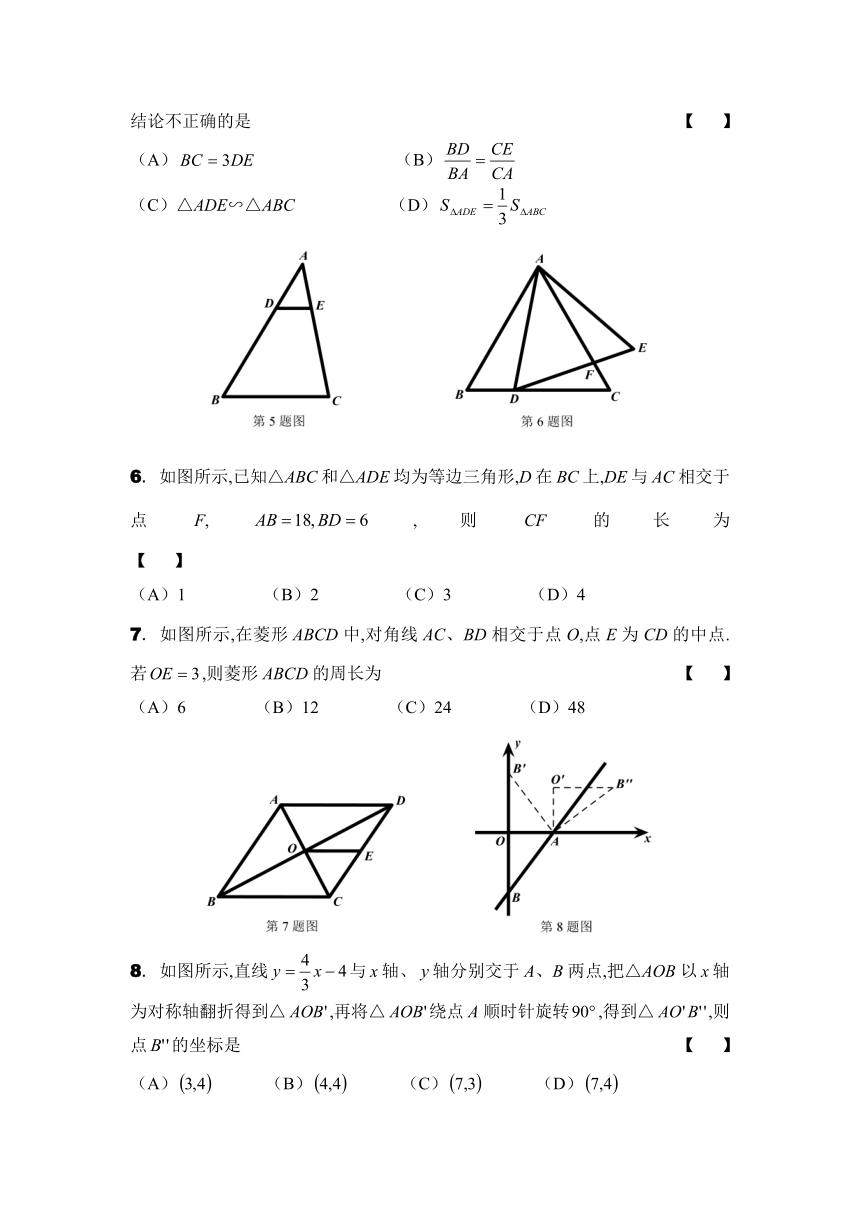
5. 如图所示,在△ABC中,点D在AB上,交AC于E,则下列结论不正确的是 【 】
(A) (B)
(C)△ADE∽△ABC (D)
6. 如图所示,已知△ABC和△ADE均为等边三角形,D在BC上,DE与AC相交于点F,,则CF的长为 【 】
(A)1 (B)2 (C)3 (D)4
7. 如图所示,在菱形ABCD中,对角线AC、BD相交于点O,点E为CD的中点.若,则菱形ABCD的周长为 【 】
(A)6 (B)12 (C)24 (D)48
8. 如图所示,直线与轴、轴分别交于A、B两点,把△AOB以轴为对称轴翻折得到△,再将△绕点A顺时针旋转,得到△,则点的坐标是 【 】
(A) (B) (C) (D)
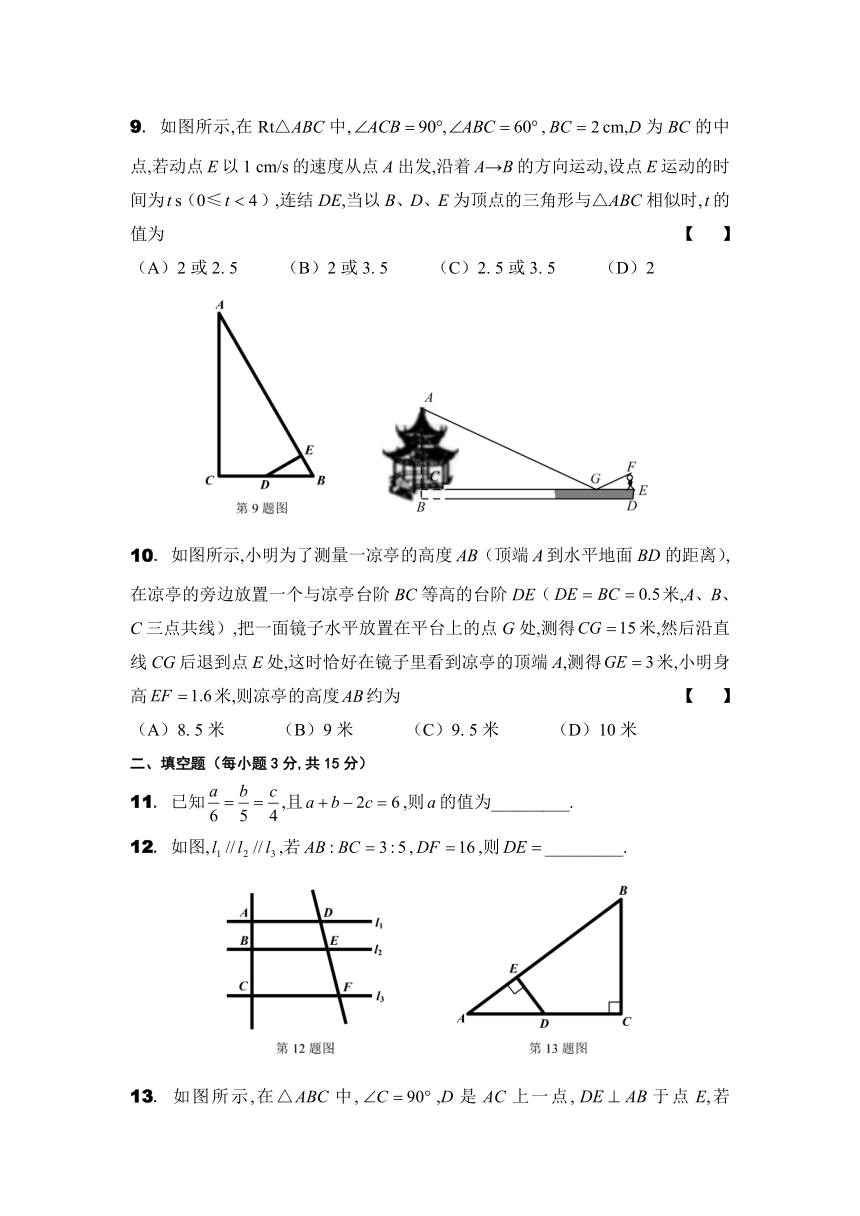
9. 如图所示,在Rt△ABC中,,cm,D为BC的中点,若动点E以1 cm/s的速度从点A出发,沿着A→B的方向运动,设点E运动的时间为s(0≤),连结DE,当以B、D、E为顶点的三角形与△ABC相似时,的值为 【 】
(A)2或2. 5 (B)2或3. 5 (C)2. 5或3. 5 (D)2
10. 如图所示,小明为了测量一凉亭的高度(顶端到水平地面BD的距离),在凉亭的旁边放置一个与凉亭台阶BC等高的台阶DE(米,A、B、C三点共线),把一面镜子水平放置在平台上的点G处,测得米,然后沿直线CG后退到点E处,这时恰好在镜子里看到凉亭的顶端A,测得米,小明身高米,则凉亭的高度AB约为 【 】
(A)8. 5米 (B)9米 (C)9. 5米 (D)10米
二、填空题(每小题3分,共15分)
11. 已知,且,则的值为_________.
12. 如图,,若,,则_________.
13. 如图所示,在△ABC中,,D是AC上一点,于点E,若,,则AD的长为_________.
14. 如图所示,在△ABC中,BE平分,,若,则AC的长为_________.
15. 如图,将矩形纸片ABCD沿EF折叠,使点B与CD的中点重合,若,则△与△的面积之比为_________.
三、解答题(共75分)
16.(9分)已知是△ABC的三边长,且.
(1)求的值;
(2)若△ABC的周长为90,求△ABC各边的长.
17.(9分)如图所示,在△ABC中,.
求证:.
18.(9分)如图所示,在正方形ABCD中,点E、F、G分别在AB、BC、CD上,且。
(1)求证:△BEF∽△CFG;
(2)若,求CG的长.
19.(9分)如图(17)所示,在边长为1个单位长度的小正方形网格中:
(1)画出△ABC向上平移6个单位长度,再向右平移5个单位长度后的△;
(2)以点B为位似中心,将△ABC放大为原来的2倍,得到△,请在网格中画出△;
(3)求△的面积.
20.(9分)如图所示,等边三角形ABC的边长为3,P为BC边上一点,D为AC边上一点,且.
(1)求证: △ABP∽△PCD;
(2)求CD的长.
21.(9分)如图(10)所示,在正方形ABCD中,M为BC上一点,F是AM的中点,,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM∽△EFA;
(2)若,求AE的长.
22.(10分)如图,正方形ABCD的边长为4,点E是BC边的中点,点P在射线AD上,过点P作于点F.
(1)求证:△PFA∽△ABE;
(2)当点P在射线AD上运动时,设,是否存在实数,使以P、F、E为顶点的三角形与△ABE相似 若存在,请求出的值;若不存在,请说明理由.
23.(11分)如图,已知矩形ABCD的边长,点P是AD上一动点(点P异于A、D两点),点Q是BC上任意一点,连结AQ、DQ,过点P作.
(1)填空:△APE∽_________, △DPF∽_________;
(2)设,△APE的面积为,△DPF的面积为,分别求出和关于的函数关系式;
(3)在边AD上是否存在这样的点P,使△PEF的面积为 若存在,求出的值;若不存在,请说明理由.
图形的相似单元测试卷
参考答案和评分标准
一、选择题(每小题3分,共30分)
题号 1 2 3 4 5
答案 B C B D D
题号 6 7 8 9 10
答案 D C C B A
二、填空题(每小题3分,共15分)
11. 12 12. 6 13. 5 14. 6 15. 16 : 9
三、解答题(共75分)
16.(9分)已知是△ABC的三边长,且.
(1)求的值;
(2)若△ABC的周长为90,求△ABC各边的长.
解:(1)设,则:
……………………………………1分
∴;
……………………………………4分
(2)∵
∴
∴
∴
……………………………………6分
∴.
……………………………………9分
17.(9分)如图所示,在△ABC中,.
求证:.
证明:∵
∴△ADG∽△AEC
∴
……………………………………3分
∵
∴△AEG∽△ABC
∴
……………………………………6分
∴
……………………………………7分
∴.
……………………………………9分
18.(9分)如图所示,在正方形ABCD中,点E、F、G分别在AB、BC、CD上,且。
(1)求证:△BEF∽△CFG;
(2)若,求CG的长.
(1)证明:∵四边形ABCD是正方形
∴
∴
∵
∴
∴
∵,
∴△BEF∽△CFG;
……………………………………5分
(2)解:∵
∴
由(1)可知: △BEF∽△CFG
∴,
∴.
……………………………………9分
19.(9分)如图(17)所示,在边长为1个单位长度的小正方形网格中:
(1)画出△ABC向上平移6个单位长度,再向右平移5个单位长度后的△;
(2)以点B为位似中心,将△ABC放大为原来的2倍,得到△,请在网格中画出△;
(3)求△的面积.
解:(1)如图(17)所示;
……………………………………3分
(2)如图(17)所示;
……………………………………6分
(3).
……………………………………9分
20.(9分)如图所示,等边三角形ABC的边长为3,P为BC边上一点,D为AC边上一点,且.
(1)求证: △ABP∽△PCD;
(2)求CD的长.
(1)证明:∵△ABC是等边三角形
∴
∵
∴
∵∵,
∴△ABP∽△PCD;
……………………………………5分
(2)解:∵
∴
……………………………………6分
由(1)可知:△ABP∽△PCD
∴
∴.
……………………………………9分
21.(9分)如图(10)所示,在正方形ABCD中,M为BC上一点,F是AM的中点,,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM∽△EFA;
(2)若,求AE的长.
(1)证明:∵四边形ABCD是正方形,
∴
……………………………………1分
∴
∴
……………………………………2分
∵,
∴△ABM∽△EFA;
……………………………………4分
(2)解:在Rt△ABM中,由勾股定理得:
……………………………………6分
∵F是AM的中点
∴
……………………………………7分
∵△ABM∽△EFA
∴
∴.
……………………………………9分
22.(10分)如图,正方形ABCD的边长为4,点E是BC边的中点,点P在射线AD上,过点P作于点F.
(1)求证:△PFA∽△ABE;
(2)当点P在射线AD上运动时,设,是否存在实数,使以P、F、E为顶点的三角形与△ABE相似 若存在,请求出的值;若不存在,请说明理由.
(1)证明:∵四边形ABCD是正方形
∴
……………………………………1分
∴
∵
∴∴
∵
∴△PFA∽△ABE;
……………………………………4分
(2)解:存在.
……………………………………5分
分为两种情况:
①当△EFP∽△ABE时,如图所示,
∴
∴四边形ABEP是矩形
∴;
……………………………………7分
②当△PFE∽△ABE时,如图所示.
∴
∵
∴
∴
∴
在Rt△ABE中,由勾股定理得:
∵
∴
∵△PFE∽△ABE
∴
∴
∴
……………………………………10分
综上所述,的值为2或5.
23.(11分)如图,已知矩形ABCD的边长,点P是AD上一动点(点P异于A、D两点),点Q是BC上任意一点,连结AQ、DQ,过点P作.
(1)填空:△APE∽_________, △DPF∽_________;
(2)设,△APE的面积为,△DPF的面积为,分别求出和关于的函数关系式;
(3)在边AD上是否存在这样的点P,使△PEF的面积为 若存在,求出的值;若不存在,请说明理由.
解:(1)△ADQ , △DAQ;
……………………………………2分
(2)∵,
∴
∵△APE∽△ADQ
∴
∴
∴………………………5分
∵△DPF∽△DAQ
∴
∴
∴;
……………………………………8分
(3)存在,理由如下:
……………………………………9分
∵
∴
∴四边形PEQF是平行四边形
∴
……………………………………10分
当时,
解之得:
……………………………………11分
∴当时,△PEF的面积为.
姓名____________ 时间:90分钟 满分:120分 总分_________
注意事项:
1. 请在试卷规定时间内作答.
2. 请注意答题规范,书写规范.
3. 请用0.5毫米黑色水笔把答案直接答在试卷上.
一、选择题(每小题3分,共30分)
1. 已知,则下列比例式成立的是 【 】
(A) (B) (C) (D)
2. 如图所示,在△ABC中,,则AC的长为 【 】
(A)6 (B)7 (C)8 (D)9
3. 如图所示,在△ABC中,点D、E分别在边AB、AC上,DE与BC不平行,添加下列条件仍不能判定△ADE∽△ACB的是 【 】
(A) (B)
(C) (D)
4. 如图所示,△ABC的中线BE、CF交于点O,
连结EF,则的值为 【 】
(A) (B) (C) (D)
5. 如图所示,在△ABC中,点D在AB上,交AC于E,则下列结论不正确的是 【 】
(A) (B)
(C)△ADE∽△ABC (D)
6. 如图所示,已知△ABC和△ADE均为等边三角形,D在BC上,DE与AC相交于点F,,则CF的长为 【 】
(A)1 (B)2 (C)3 (D)4
7. 如图所示,在菱形ABCD中,对角线AC、BD相交于点O,点E为CD的中点.若,则菱形ABCD的周长为 【 】
(A)6 (B)12 (C)24 (D)48
8. 如图所示,直线与轴、轴分别交于A、B两点,把△AOB以轴为对称轴翻折得到△,再将△绕点A顺时针旋转,得到△,则点的坐标是 【 】
(A) (B) (C) (D)
9. 如图所示,在Rt△ABC中,,cm,D为BC的中点,若动点E以1 cm/s的速度从点A出发,沿着A→B的方向运动,设点E运动的时间为s(0≤),连结DE,当以B、D、E为顶点的三角形与△ABC相似时,的值为 【 】
(A)2或2. 5 (B)2或3. 5 (C)2. 5或3. 5 (D)2
10. 如图所示,小明为了测量一凉亭的高度(顶端到水平地面BD的距离),在凉亭的旁边放置一个与凉亭台阶BC等高的台阶DE(米,A、B、C三点共线),把一面镜子水平放置在平台上的点G处,测得米,然后沿直线CG后退到点E处,这时恰好在镜子里看到凉亭的顶端A,测得米,小明身高米,则凉亭的高度AB约为 【 】
(A)8. 5米 (B)9米 (C)9. 5米 (D)10米
二、填空题(每小题3分,共15分)
11. 已知,且,则的值为_________.
12. 如图,,若,,则_________.
13. 如图所示,在△ABC中,,D是AC上一点,于点E,若,,则AD的长为_________.
14. 如图所示,在△ABC中,BE平分,,若,则AC的长为_________.
15. 如图,将矩形纸片ABCD沿EF折叠,使点B与CD的中点重合,若,则△与△的面积之比为_________.
三、解答题(共75分)
16.(9分)已知是△ABC的三边长,且.
(1)求的值;
(2)若△ABC的周长为90,求△ABC各边的长.
17.(9分)如图所示,在△ABC中,.
求证:.
18.(9分)如图所示,在正方形ABCD中,点E、F、G分别在AB、BC、CD上,且。
(1)求证:△BEF∽△CFG;
(2)若,求CG的长.
19.(9分)如图(17)所示,在边长为1个单位长度的小正方形网格中:
(1)画出△ABC向上平移6个单位长度,再向右平移5个单位长度后的△;
(2)以点B为位似中心,将△ABC放大为原来的2倍,得到△,请在网格中画出△;
(3)求△的面积.
20.(9分)如图所示,等边三角形ABC的边长为3,P为BC边上一点,D为AC边上一点,且.
(1)求证: △ABP∽△PCD;
(2)求CD的长.
21.(9分)如图(10)所示,在正方形ABCD中,M为BC上一点,F是AM的中点,,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM∽△EFA;
(2)若,求AE的长.
22.(10分)如图,正方形ABCD的边长为4,点E是BC边的中点,点P在射线AD上,过点P作于点F.
(1)求证:△PFA∽△ABE;
(2)当点P在射线AD上运动时,设,是否存在实数,使以P、F、E为顶点的三角形与△ABE相似 若存在,请求出的值;若不存在,请说明理由.
23.(11分)如图,已知矩形ABCD的边长,点P是AD上一动点(点P异于A、D两点),点Q是BC上任意一点,连结AQ、DQ,过点P作.
(1)填空:△APE∽_________, △DPF∽_________;
(2)设,△APE的面积为,△DPF的面积为,分别求出和关于的函数关系式;
(3)在边AD上是否存在这样的点P,使△PEF的面积为 若存在,求出的值;若不存在,请说明理由.
图形的相似单元测试卷
参考答案和评分标准
一、选择题(每小题3分,共30分)
题号 1 2 3 4 5
答案 B C B D D
题号 6 7 8 9 10
答案 D C C B A
二、填空题(每小题3分,共15分)
11. 12 12. 6 13. 5 14. 6 15. 16 : 9
三、解答题(共75分)
16.(9分)已知是△ABC的三边长,且.
(1)求的值;
(2)若△ABC的周长为90,求△ABC各边的长.
解:(1)设,则:
……………………………………1分
∴;
……………………………………4分
(2)∵
∴
∴
∴
……………………………………6分
∴.
……………………………………9分
17.(9分)如图所示,在△ABC中,.
求证:.
证明:∵
∴△ADG∽△AEC
∴
……………………………………3分
∵
∴△AEG∽△ABC
∴
……………………………………6分
∴
……………………………………7分
∴.
……………………………………9分
18.(9分)如图所示,在正方形ABCD中,点E、F、G分别在AB、BC、CD上,且。
(1)求证:△BEF∽△CFG;
(2)若,求CG的长.
(1)证明:∵四边形ABCD是正方形
∴
∴
∵
∴
∴
∵,
∴△BEF∽△CFG;
……………………………………5分
(2)解:∵
∴
由(1)可知: △BEF∽△CFG
∴,
∴.
……………………………………9分
19.(9分)如图(17)所示,在边长为1个单位长度的小正方形网格中:
(1)画出△ABC向上平移6个单位长度,再向右平移5个单位长度后的△;
(2)以点B为位似中心,将△ABC放大为原来的2倍,得到△,请在网格中画出△;
(3)求△的面积.
解:(1)如图(17)所示;
……………………………………3分
(2)如图(17)所示;
……………………………………6分
(3).
……………………………………9分
20.(9分)如图所示,等边三角形ABC的边长为3,P为BC边上一点,D为AC边上一点,且.
(1)求证: △ABP∽△PCD;
(2)求CD的长.
(1)证明:∵△ABC是等边三角形
∴
∵
∴
∵∵,
∴△ABP∽△PCD;
……………………………………5分
(2)解:∵
∴
……………………………………6分
由(1)可知:△ABP∽△PCD
∴
∴.
……………………………………9分
21.(9分)如图(10)所示,在正方形ABCD中,M为BC上一点,F是AM的中点,,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM∽△EFA;
(2)若,求AE的长.
(1)证明:∵四边形ABCD是正方形,
∴
……………………………………1分
∴
∴
……………………………………2分
∵,
∴△ABM∽△EFA;
……………………………………4分
(2)解:在Rt△ABM中,由勾股定理得:
……………………………………6分
∵F是AM的中点
∴
……………………………………7分
∵△ABM∽△EFA
∴
∴.
……………………………………9分
22.(10分)如图,正方形ABCD的边长为4,点E是BC边的中点,点P在射线AD上,过点P作于点F.
(1)求证:△PFA∽△ABE;
(2)当点P在射线AD上运动时,设,是否存在实数,使以P、F、E为顶点的三角形与△ABE相似 若存在,请求出的值;若不存在,请说明理由.
(1)证明:∵四边形ABCD是正方形
∴
……………………………………1分
∴
∵
∴∴
∵
∴△PFA∽△ABE;
……………………………………4分
(2)解:存在.
……………………………………5分
分为两种情况:
①当△EFP∽△ABE时,如图所示,
∴
∴四边形ABEP是矩形
∴;
……………………………………7分
②当△PFE∽△ABE时,如图所示.
∴
∵
∴
∴
∴
在Rt△ABE中,由勾股定理得:
∵
∴
∵△PFE∽△ABE
∴
∴
∴
……………………………………10分
综上所述,的值为2或5.
23.(11分)如图,已知矩形ABCD的边长,点P是AD上一动点(点P异于A、D两点),点Q是BC上任意一点,连结AQ、DQ,过点P作.
(1)填空:△APE∽_________, △DPF∽_________;
(2)设,△APE的面积为,△DPF的面积为,分别求出和关于的函数关系式;
(3)在边AD上是否存在这样的点P,使△PEF的面积为 若存在,求出的值;若不存在,请说明理由.
解:(1)△ADQ , △DAQ;
……………………………………2分
(2)∵,
∴
∵△APE∽△ADQ
∴
∴
∴………………………5分
∵△DPF∽△DAQ
∴
∴
∴;
……………………………………8分
(3)存在,理由如下:
……………………………………9分
∵
∴
∴四边形PEQF是平行四边形
∴
……………………………………10分
当时,
解之得:
……………………………………11分
∴当时,△PEF的面积为.
