八年级下学期18.3.2相似三角形的识别[下学期]
文档属性
| 名称 | 八年级下学期18.3.2相似三角形的识别[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 565.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-22 08:53:00 | ||
图片预览






文档简介
课件22张PPT。1我们现在识别两个三角形是否相似,必须要知道它们的对应角是否相等,对应边是否成比例.那么是否存在识别两个三角形相似的简便方法呢?218.3相似三角形
(二)相似三角形的识别3观察你与你同伴的直角三角尺,同样角度(30°与60°,或45°与45°)的三角尺看起来是相似的.这样从直观来看,一个三角形的三个角分别与另一个三角形的三个角对应相等时,它们就“应该”相似了,确实这样吗?4探 索
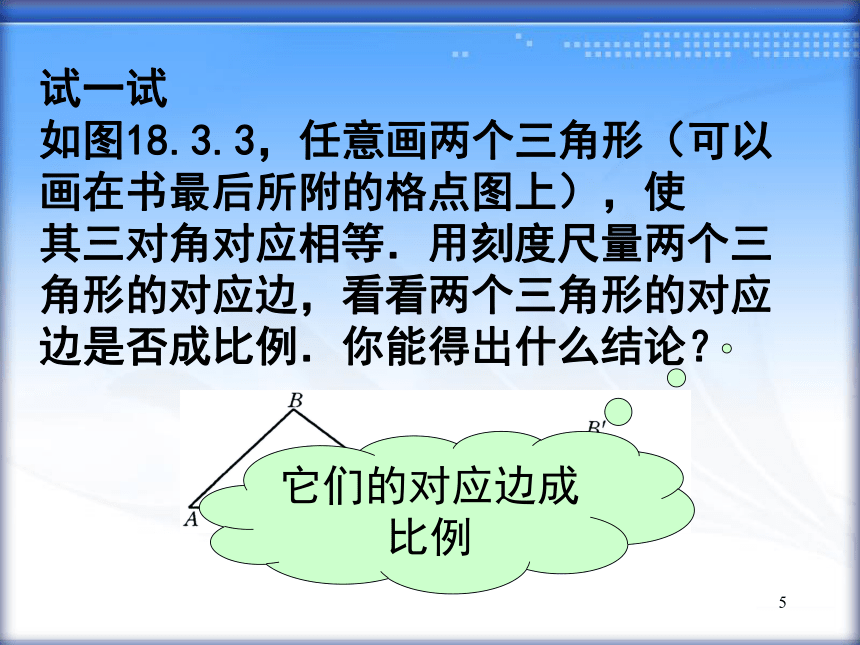
如果一个三角形的三个角分别与另一个三角形的三个角对应相等,那么它们相似吗?5试一试
如图18.3.3,任意画两个三角形(可以画在书最后所附的格点图上),使
其三对角对应相等.用刻度尺量两个三角形的对应边,看看两个三角形的对应边是否成比例.你能得出什么结论?它们的对应边成比例 6即: 如果一个三角形的三个角分别
与另一个三角形的三个角对应相等,那么这两个三角形_______.
一定需三个角吗?根据三角形内角和定理,我们知道如果两个三角形有两对角对应相等,那么第三对角也一定对应相等.
于是,我们可以得到识别两个三角形相似的一个较为简便的方法:
相似7思 考
如果两个三角形仅有一对角是对应相等的,那么它们是否一定相似?
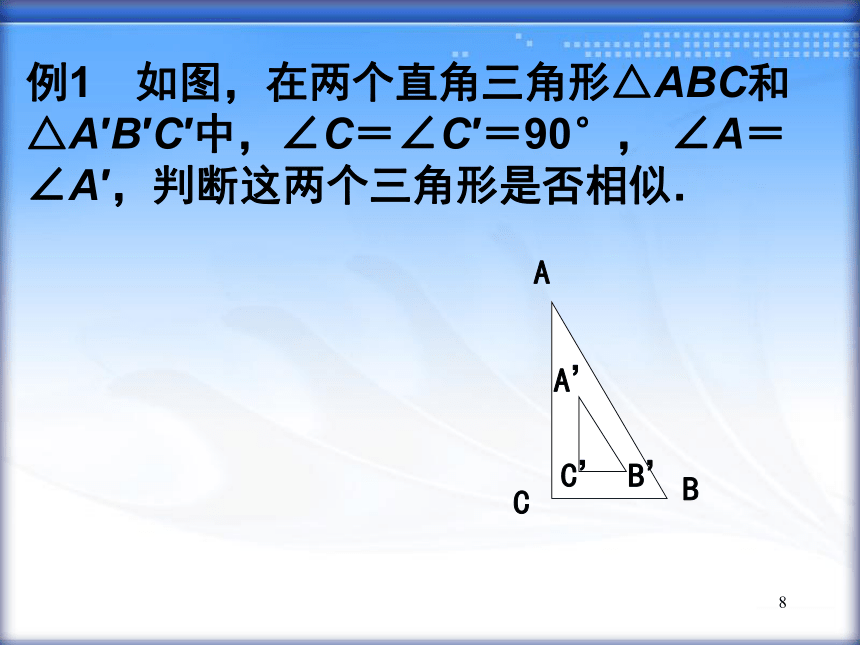
1.如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.相似三角形的识别方法:8例1 如图,在两个直角三角形△ABC和△A′B′C′中,∠C=∠C′=90°, ∠A=∠A′,判断这两个三角形是否相似.
9
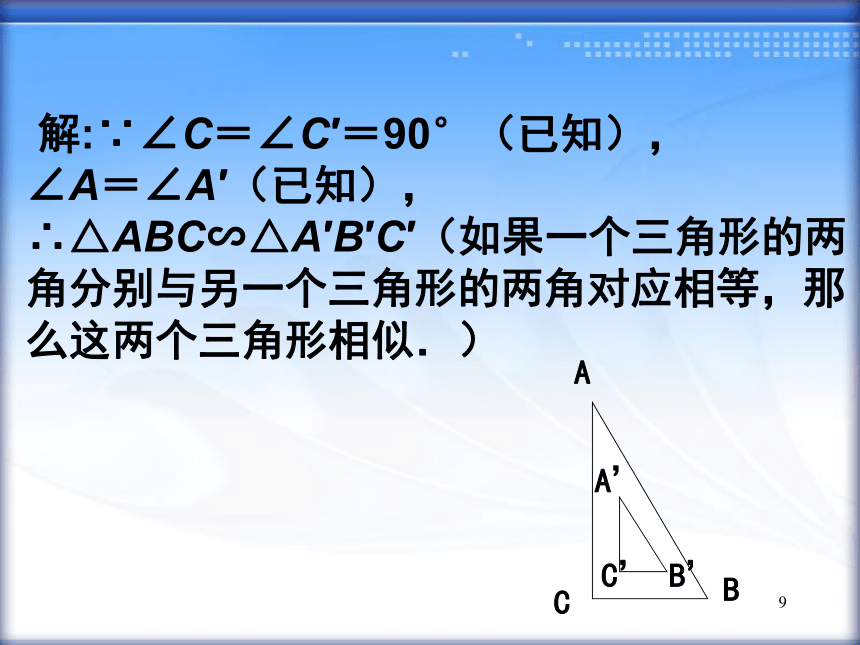
解:∵∠C=∠C′=90°(已知),
∠A=∠A′(已知),
∴△ABC∽△A′B′C′(如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.)
10例2 如图18.3.5,△ABC中,DE∥BC,EF∥AB,试说明△ADE∽△EFC.11解:∵ DE∥BC,EF∥AB(已知),
∴∠ADE=∠B=∠EFC(两直线平行,同位 角相等),
∠AED=∠C.(两直线平行,同位角相等)
∴ △ADE∽△EFC. (如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.)12观察图18.3.6,如果有一点E在边AC上,那么点E应该在什么位置才能使△ADE与△ABC相似呢?图中两个三角形的一组对应边AD与AB的长度的比值为 .将点E由点A开始在AC上移动,可以发现当
AE =___AC时,△ADE与△ABC相似.此时 =
_______.13探 索
如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似吗?14做一做 : 利用刻度尺和量角器画两个三角形,使它们的两条对应边成比例,并且夹角相等.量一量第三条对应边的长,计算它们的比与前两条对应边的比是否相等?另两个角是否对应相等?你能得出什么结论?
15我们可以发现这两个三角形相似.这样我们又有了一种识别两个三角形是否相似的方法: 2.如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似. 16 例3 判断图18.3.7中△AEB和△FEC是否相似?17解 ∵∠AEB=∠FEC(对顶角相等),
= =1.5(已知),
= =1.5(已知),
= ,
∴ △AEB∽△FEC(如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似.) 18例4。下列每个图形中,是否存在相似三角形?若存在,用字母表示出来,并写出对应的比例式。19A4EDCEABBCD2632021课堂小结:相似三角形的识别方法:1。定义:对应角相等,对应边成比例的三角形相似。2。平行于三角形的一边的直线和其它两边(或两边的延长线)相交,所构成的三角形相似.224。如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似. 3。如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.
(二)相似三角形的识别3观察你与你同伴的直角三角尺,同样角度(30°与60°,或45°与45°)的三角尺看起来是相似的.这样从直观来看,一个三角形的三个角分别与另一个三角形的三个角对应相等时,它们就“应该”相似了,确实这样吗?4探 索
如果一个三角形的三个角分别与另一个三角形的三个角对应相等,那么它们相似吗?5试一试
如图18.3.3,任意画两个三角形(可以画在书最后所附的格点图上),使
其三对角对应相等.用刻度尺量两个三角形的对应边,看看两个三角形的对应边是否成比例.你能得出什么结论?它们的对应边成比例 6即: 如果一个三角形的三个角分别
与另一个三角形的三个角对应相等,那么这两个三角形_______.
一定需三个角吗?根据三角形内角和定理,我们知道如果两个三角形有两对角对应相等,那么第三对角也一定对应相等.
于是,我们可以得到识别两个三角形相似的一个较为简便的方法:
相似7思 考
如果两个三角形仅有一对角是对应相等的,那么它们是否一定相似?
1.如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.相似三角形的识别方法:8例1 如图,在两个直角三角形△ABC和△A′B′C′中,∠C=∠C′=90°, ∠A=∠A′,判断这两个三角形是否相似.
9
解:∵∠C=∠C′=90°(已知),
∠A=∠A′(已知),
∴△ABC∽△A′B′C′(如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.)
10例2 如图18.3.5,△ABC中,DE∥BC,EF∥AB,试说明△ADE∽△EFC.11解:∵ DE∥BC,EF∥AB(已知),
∴∠ADE=∠B=∠EFC(两直线平行,同位 角相等),
∠AED=∠C.(两直线平行,同位角相等)
∴ △ADE∽△EFC. (如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.)12观察图18.3.6,如果有一点E在边AC上,那么点E应该在什么位置才能使△ADE与△ABC相似呢?图中两个三角形的一组对应边AD与AB的长度的比值为 .将点E由点A开始在AC上移动,可以发现当
AE =___AC时,△ADE与△ABC相似.此时 =
_______.13探 索
如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似吗?14做一做 : 利用刻度尺和量角器画两个三角形,使它们的两条对应边成比例,并且夹角相等.量一量第三条对应边的长,计算它们的比与前两条对应边的比是否相等?另两个角是否对应相等?你能得出什么结论?
15我们可以发现这两个三角形相似.这样我们又有了一种识别两个三角形是否相似的方法: 2.如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似. 16 例3 判断图18.3.7中△AEB和△FEC是否相似?17解 ∵∠AEB=∠FEC(对顶角相等),
= =1.5(已知),
= =1.5(已知),
= ,
∴ △AEB∽△FEC(如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似.) 18例4。下列每个图形中,是否存在相似三角形?若存在,用字母表示出来,并写出对应的比例式。19A4EDCEABBCD2632021课堂小结:相似三角形的识别方法:1。定义:对应角相等,对应边成比例的三角形相似。2。平行于三角形的一边的直线和其它两边(或两边的延长线)相交,所构成的三角形相似.224。如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似. 3。如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.
