相似三角形的识别(1)[下学期]
图片预览


文档简介
课件18张PPT。§18.3.3相似三角形的识别(1)百官中学初二数学组三个角对应_______,三条边对应——————的两个
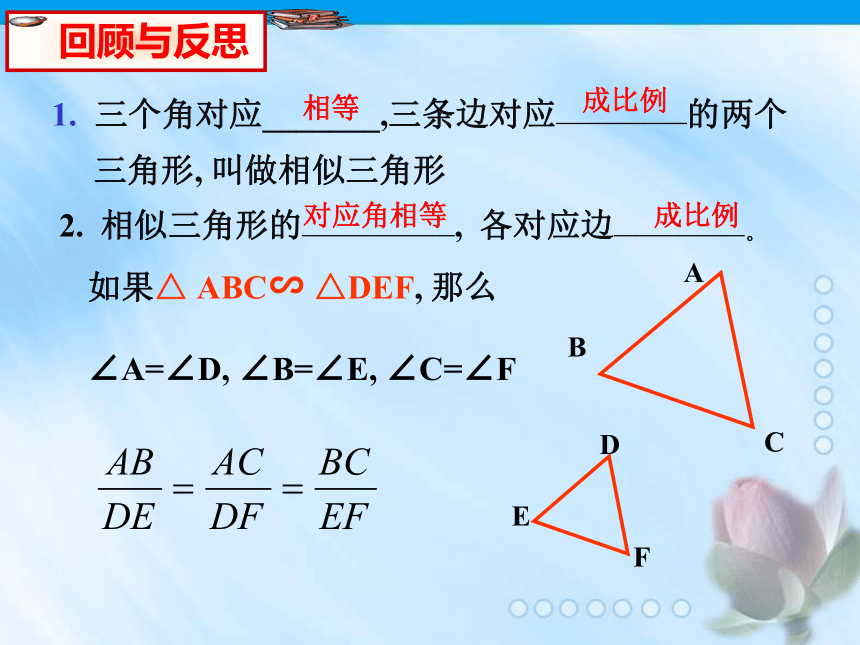
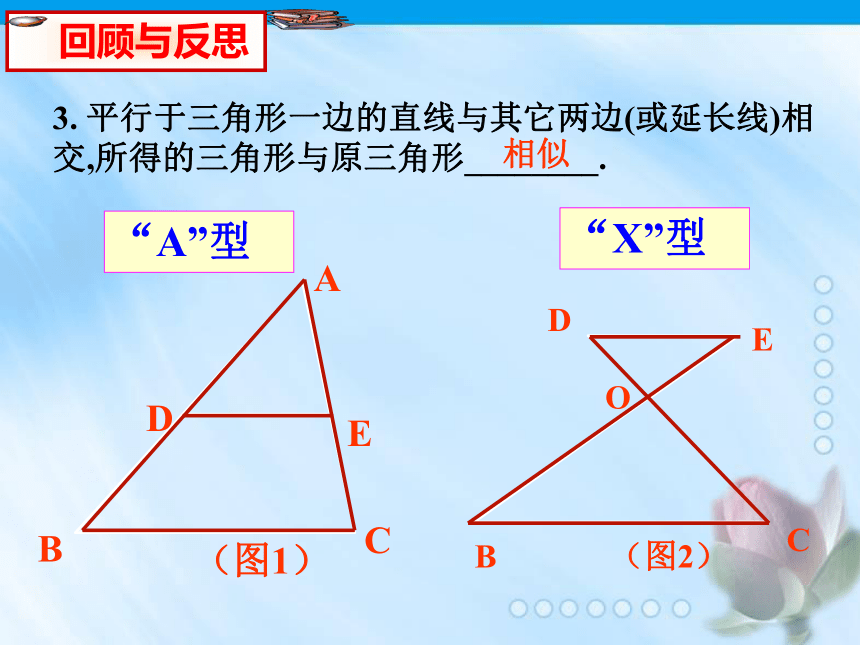
三角形, 叫做相似三角形 相等成比例2. 相似三角形的———————, 各对应边——————。对应角相等成比例如果△ ABC∽ △DEF, 那么∠A=∠D, ∠B=∠E, ∠C=∠F3. 平行于三角形一边的直线与其它两边(或延长线)相交,所得的三角形与原三角形________.相似“A”型 “X”型 我们现在识别两个三角形是否相似,必须要知道它们的对应角是否相等,对应边是否成比例.那么是否存在识别两个三角形相似的简便方法呢? 请观察你与你同伴的直角三角尺,同样角度(30°与60°,或45°与45°)的三角尺看起来是否相似?确实这样吗?识 别 方 法 探 讨:动手画一画两个三对角相等的三角形多媒体演示结论:如果一个三角形的三个角分别与另
一个三角形的三个角对应相等,那么这两
个三角形________.相似根据三角形内角和定理,我们知道如果两个三角形有两对角对应相等,那么第三对角也一定对应相等.
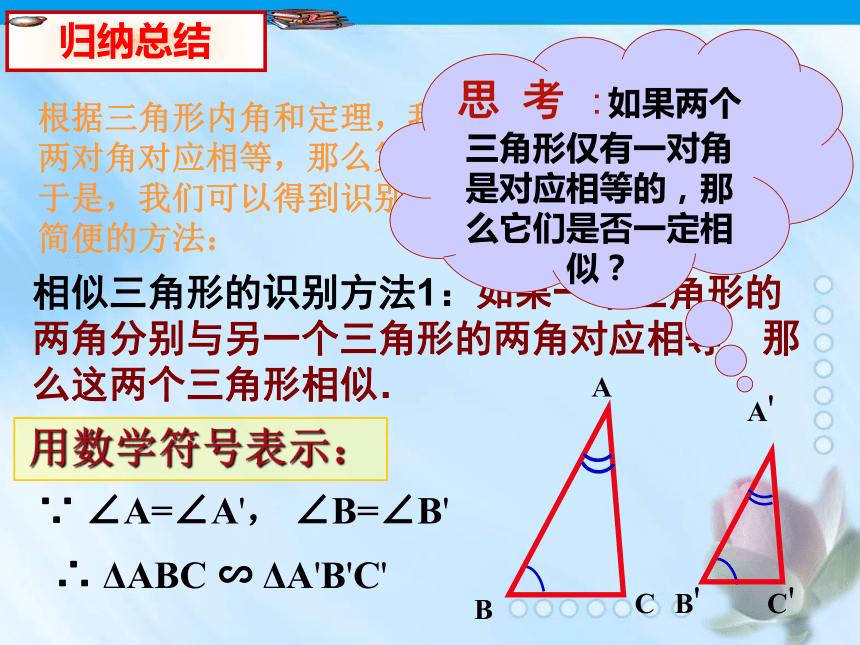
于是,我们可以得到识别两个三角形相似的一个较为简便的方法:相似三角形的识别方法1:如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.用数学符号表示:∵ ∠A=∠A', ∠B=∠B'∴ ΔABC ∽ ΔA'B'C'思 考 :如果两个三角形仅有一对角是对应相等的,那么它们是否一定相似?
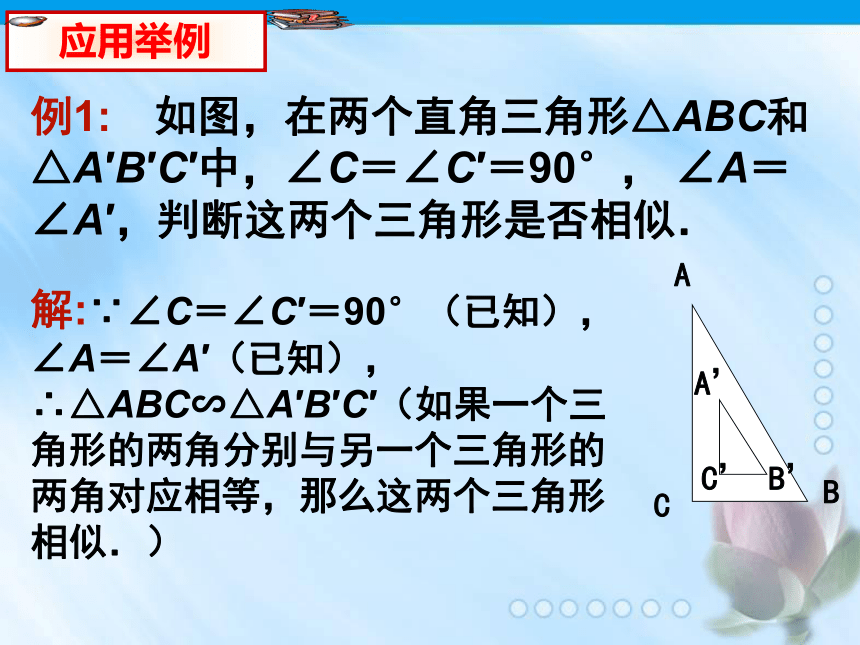
CC'例1: 如图,在两个直角三角形△ABC和△A′B′C′中,∠C=∠C′=90°, ∠A=∠A′,判断这两个三角形是否相似.解:∵∠C=∠C′=90°(已知),
∠A=∠A′(已知),
∴△ABC∽△A′B′C′(如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.) 例2: 如图18.3.5,△ABC中,DE∥BC,EF∥AB,试说明△ADE∽△EFC.解:∵ DE∥BC,EF∥AB(已知),∴∠ADE=∠B=∠EFC(两直线平行,同位角相等), ∠AED=∠C.(两直线平行,同位角相等)∴ △ADE∽△EFC. (如果一个三角形的两个角分别与另一个三角形的两个角对应相等,那么这两个三角形相似.)想一想:如果点D是AB的中点,那么点E是边AC的中点吗?DE和BC又有什么关系?1、根据给出的条件,按相应顺序写出相似三角形,并说明理由(要求步步有依据)(2) DE∥BC
△ ∽ △______ △ ∽ △ __________. (1)DE∥BC ADE ABCADE ACB2、已知直角三角形ABC中,∠ACB=900,CD⊥AB于点D,则:
__________∽__________∽__________.3、如图、在△ABC中,边AB、AC上的高CE、BD相交于点P,请找出图中所有的相似三角形。△ABC△ACD△CBD△ABD与△ACE△BEP与△CDP4、如图,在△ABC中,DG∥EH∥FI∥BC,
(1)请找出图中所有的相似三角形;
(2)如果AD=1,DB=3,那么DG:BC=___________。△ADG∽△AEH∽△AFI∽△ABC1:4已知: Rt△ABC 与 Rt△DFE中,∠B与∠F为直角(如图所示)。问能否分别将这两个三角形各分割成两个三角形,使△ABC所分成的两个三角形与△DEF所分成的两个三角形相似?
请设计出一种分割方案,并加以分析.△ABM∽△FEN△MBC∽△NDF 如图,在△ABC中,∠1=∠2=∠3,试说明△ABC∽△DEF解:∵∠FDE=∠DAC+∠3
∠1=∠3∴∠FDE=∠DAC+∠1=∠BAC∵∠DFE=∠ABF+∠1
∠1=∠2∴∠DFE=∠ABF+∠2=∠ABC∵∠FDE=∠BAC;∠DFE=∠ABC。∴ △ABC∽△DEF( ? )课堂小结 通过本堂课的学习,我们已经学会了相似三角形的几种识别方法?1、平行于三角形一边的直线与其它两边(或延长线)相交,所得的三角形与原三角形相似。2、如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似。再见 试着用课本第157页的格点画两个三角形。
要求: (用铅笔)有2组内角分别对应相等.(如下图)观察 (或测量计算):
这2个三角形的对应边的比值是否相同?1243∠1=∠2
∠3=∠4
三角形, 叫做相似三角形 相等成比例2. 相似三角形的———————, 各对应边——————。对应角相等成比例如果△ ABC∽ △DEF, 那么∠A=∠D, ∠B=∠E, ∠C=∠F3. 平行于三角形一边的直线与其它两边(或延长线)相交,所得的三角形与原三角形________.相似“A”型 “X”型 我们现在识别两个三角形是否相似,必须要知道它们的对应角是否相等,对应边是否成比例.那么是否存在识别两个三角形相似的简便方法呢? 请观察你与你同伴的直角三角尺,同样角度(30°与60°,或45°与45°)的三角尺看起来是否相似?确实这样吗?识 别 方 法 探 讨:动手画一画两个三对角相等的三角形多媒体演示结论:如果一个三角形的三个角分别与另
一个三角形的三个角对应相等,那么这两
个三角形________.相似根据三角形内角和定理,我们知道如果两个三角形有两对角对应相等,那么第三对角也一定对应相等.
于是,我们可以得到识别两个三角形相似的一个较为简便的方法:相似三角形的识别方法1:如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.用数学符号表示:∵ ∠A=∠A', ∠B=∠B'∴ ΔABC ∽ ΔA'B'C'思 考 :如果两个三角形仅有一对角是对应相等的,那么它们是否一定相似?
CC'例1: 如图,在两个直角三角形△ABC和△A′B′C′中,∠C=∠C′=90°, ∠A=∠A′,判断这两个三角形是否相似.解:∵∠C=∠C′=90°(已知),
∠A=∠A′(已知),
∴△ABC∽△A′B′C′(如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.) 例2: 如图18.3.5,△ABC中,DE∥BC,EF∥AB,试说明△ADE∽△EFC.解:∵ DE∥BC,EF∥AB(已知),∴∠ADE=∠B=∠EFC(两直线平行,同位角相等), ∠AED=∠C.(两直线平行,同位角相等)∴ △ADE∽△EFC. (如果一个三角形的两个角分别与另一个三角形的两个角对应相等,那么这两个三角形相似.)想一想:如果点D是AB的中点,那么点E是边AC的中点吗?DE和BC又有什么关系?1、根据给出的条件,按相应顺序写出相似三角形,并说明理由(要求步步有依据)(2) DE∥BC
△ ∽ △______ △ ∽ △ __________. (1)DE∥BC ADE ABCADE ACB2、已知直角三角形ABC中,∠ACB=900,CD⊥AB于点D,则:
__________∽__________∽__________.3、如图、在△ABC中,边AB、AC上的高CE、BD相交于点P,请找出图中所有的相似三角形。△ABC△ACD△CBD△ABD与△ACE△BEP与△CDP4、如图,在△ABC中,DG∥EH∥FI∥BC,
(1)请找出图中所有的相似三角形;
(2)如果AD=1,DB=3,那么DG:BC=___________。△ADG∽△AEH∽△AFI∽△ABC1:4已知: Rt△ABC 与 Rt△DFE中,∠B与∠F为直角(如图所示)。问能否分别将这两个三角形各分割成两个三角形,使△ABC所分成的两个三角形与△DEF所分成的两个三角形相似?
请设计出一种分割方案,并加以分析.△ABM∽△FEN△MBC∽△NDF 如图,在△ABC中,∠1=∠2=∠3,试说明△ABC∽△DEF解:∵∠FDE=∠DAC+∠3
∠1=∠3∴∠FDE=∠DAC+∠1=∠BAC∵∠DFE=∠ABF+∠1
∠1=∠2∴∠DFE=∠ABF+∠2=∠ABC∵∠FDE=∠BAC;∠DFE=∠ABC。∴ △ABC∽△DEF( ? )课堂小结 通过本堂课的学习,我们已经学会了相似三角形的几种识别方法?1、平行于三角形一边的直线与其它两边(或延长线)相交,所得的三角形与原三角形相似。2、如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似。再见 试着用课本第157页的格点画两个三角形。
要求: (用铅笔)有2组内角分别对应相等.(如下图)观察 (或测量计算):
这2个三角形的对应边的比值是否相同?1243∠1=∠2
∠3=∠4
