相似三角形识别的复习[下学期]
图片预览

文档简介
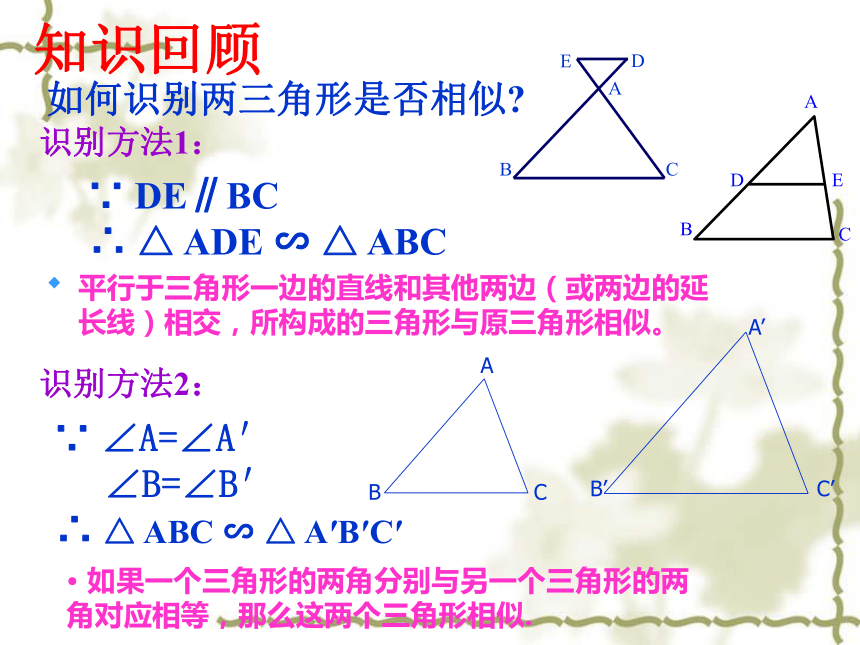
课件11张PPT。相似三角形的复习如何识别两三角形是否相似?知识回顾 ∵ DE∥BC
∴ △ ADE ∽ △ ABC 识别方法1:识别方法2: ∵ ∠A=∠A′
∠B=∠B′
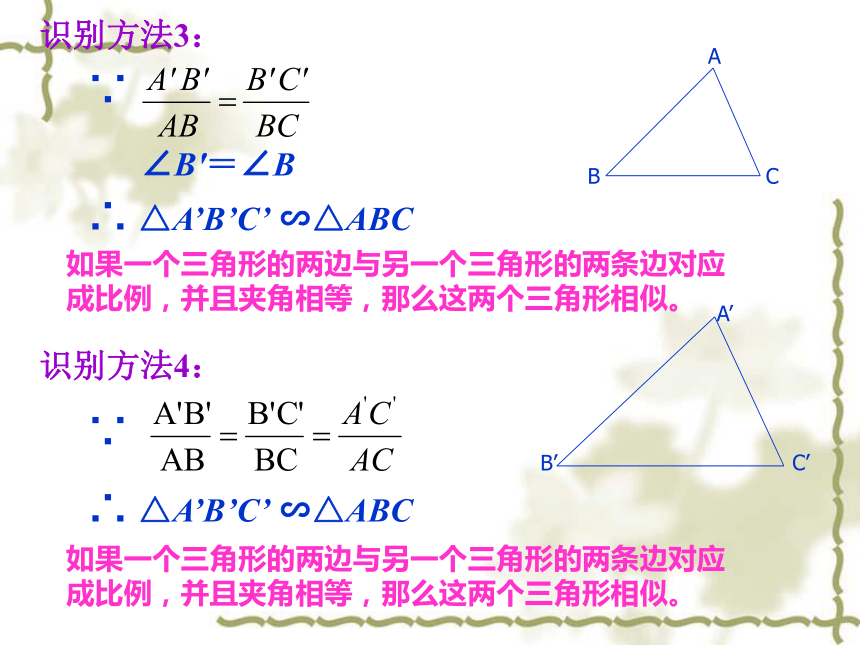
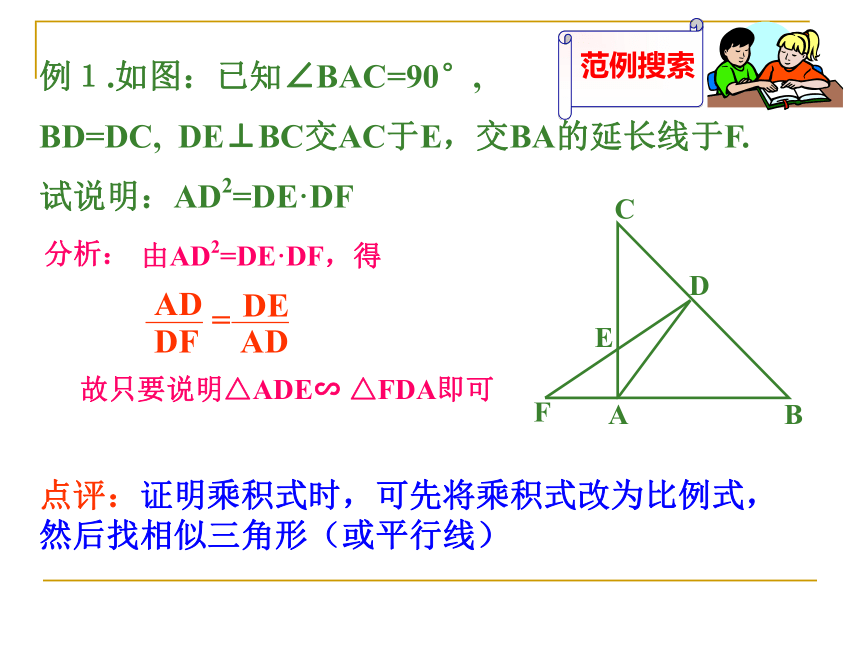
∴ △ ABC ∽ △ A′B′C′平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。 如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.如果一个三角形的两边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似。识别方法3:如果一个三角形的两边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似。识别方法4:例1.如图:已知∠BAC=90°,
BD=DC, DE⊥BC交AC于E,交BA的延长线于F.
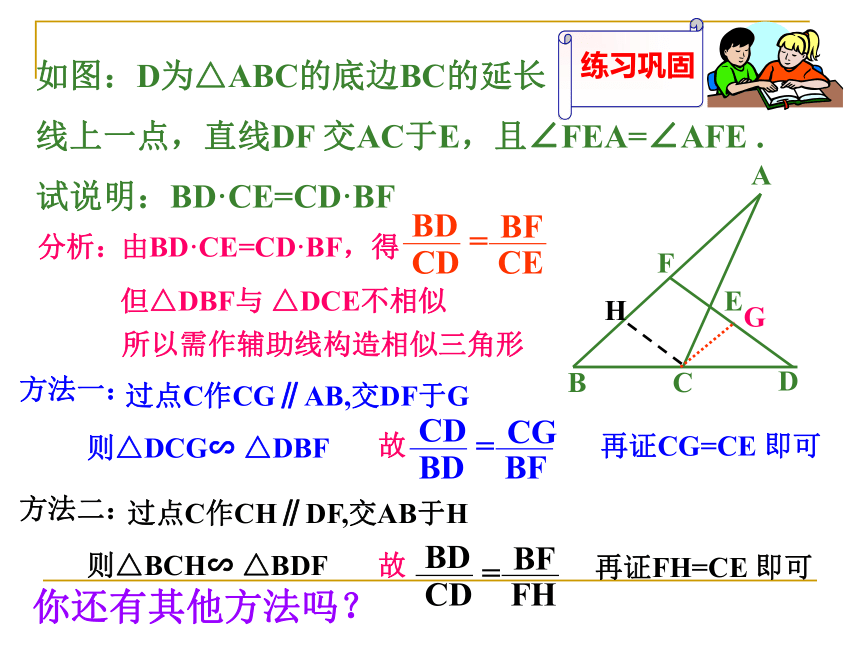
试说明:AD2=DE·DF由AD2=DE·DF,得故只要说明△ADE∽ △FDA即可分析:点评:证明乘积式时,可先将乘积式改为比例式,然后找相似三角形(或平行线)如图:D为△ABC的底边BC的延长
线上一点,直线DF 交AC于E,且∠FEA=∠AFE .
试说明:BD·CE=CD·BF方法一:过点C作CG∥AB,交DF于G 则△BCH∽ △BDF 再证CG=CE 即可故方法二:过点C作CH∥DF,交AB于H 故再证FH=CE 即可则△DCG∽ △DBF 你还有其他方法吗?例2. 如图:在Rt△ABC中,有正方形 DEFG,
且E、F在斜边BC上,D、G分别在AB、AC上.
试说明:EF2=BE·FC解:又∵ ∠B+∠C=90°,∠B+∠BDE=90°点评:证明共线的线段比例式时,将某些线段用其他线段代替,以便构成相似三角形.这是证明比例式和乘积式的常用方法之一.小 结1、判定两个三角形相似的方法(1)
(2)
(3)
(4)
(5)两角对应相等,两三角形相似两边对应成比例且夹角相等,两三角形相似三边对应成比例,两三角形相似直角边和斜边对应成比例,两直角三角形相似2、证比例式(或乘积式)的常用方法证明乘积式时,可先将乘积式改为比例式,然后找相似三角形(或平行线)3、证同一直线上的线段的比例式(或乘积式)的常用技巧证明共线的线段比例式时,将某些线段用其他线段代替,以便构成相似三角形. 这是证明比例式和乘积式的常用方法之一.平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似探究题1.如图在梯形ABCD中,AD∥BC,
∠A=90°,BD⊥ DC,
试问:
⑴请你猜想图中有相似三角形吗?
请写出来,并说明理由。
⑵如果AD= 3,BC= 5,你能求出哪些线段的长?说明:本题是结论探究题。一般是由给定的已知条件探求相应的结论,解题时往往要求充分利用条件进行大胆而合理的猜想,发现规律,得出结论.2.如图已知∠1=∠2,若再增加一个条
件能使结论AB·ED=AD·BC成立,则这
个条件可以是_________________。探究题分析:
①从角的角度思考:∠D=∠B或∠AED=∠C② 从边的角度思考:AD:AB=AE:AC说明:本题是条件探究题。一般是由给定的结论反过来探究命题成立应具备的条件.已知正方形ABCD的边长是1,P是CD边的
中点,点Q在线段BC上,当Q在什么位置时,ΔADP与
以Q,C,P为顶点的三角形相似?尝试挑战②从ΔADP∽ΔPCQ的角度思考;分 析:
①从ΔADP∽ΔQCP的角度思考;再见
∴ △ ADE ∽ △ ABC 识别方法1:识别方法2: ∵ ∠A=∠A′
∠B=∠B′
∴ △ ABC ∽ △ A′B′C′平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。 如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.如果一个三角形的两边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似。识别方法3:如果一个三角形的两边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似。识别方法4:例1.如图:已知∠BAC=90°,
BD=DC, DE⊥BC交AC于E,交BA的延长线于F.
试说明:AD2=DE·DF由AD2=DE·DF,得故只要说明△ADE∽ △FDA即可分析:点评:证明乘积式时,可先将乘积式改为比例式,然后找相似三角形(或平行线)如图:D为△ABC的底边BC的延长
线上一点,直线DF 交AC于E,且∠FEA=∠AFE .
试说明:BD·CE=CD·BF方法一:过点C作CG∥AB,交DF于G 则△BCH∽ △BDF 再证CG=CE 即可故方法二:过点C作CH∥DF,交AB于H 故再证FH=CE 即可则△DCG∽ △DBF 你还有其他方法吗?例2. 如图:在Rt△ABC中,有正方形 DEFG,
且E、F在斜边BC上,D、G分别在AB、AC上.
试说明:EF2=BE·FC解:又∵ ∠B+∠C=90°,∠B+∠BDE=90°点评:证明共线的线段比例式时,将某些线段用其他线段代替,以便构成相似三角形.这是证明比例式和乘积式的常用方法之一.小 结1、判定两个三角形相似的方法(1)
(2)
(3)
(4)
(5)两角对应相等,两三角形相似两边对应成比例且夹角相等,两三角形相似三边对应成比例,两三角形相似直角边和斜边对应成比例,两直角三角形相似2、证比例式(或乘积式)的常用方法证明乘积式时,可先将乘积式改为比例式,然后找相似三角形(或平行线)3、证同一直线上的线段的比例式(或乘积式)的常用技巧证明共线的线段比例式时,将某些线段用其他线段代替,以便构成相似三角形. 这是证明比例式和乘积式的常用方法之一.平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似探究题1.如图在梯形ABCD中,AD∥BC,
∠A=90°,BD⊥ DC,
试问:
⑴请你猜想图中有相似三角形吗?
请写出来,并说明理由。
⑵如果AD= 3,BC= 5,你能求出哪些线段的长?说明:本题是结论探究题。一般是由给定的已知条件探求相应的结论,解题时往往要求充分利用条件进行大胆而合理的猜想,发现规律,得出结论.2.如图已知∠1=∠2,若再增加一个条
件能使结论AB·ED=AD·BC成立,则这
个条件可以是_________________。探究题分析:
①从角的角度思考:∠D=∠B或∠AED=∠C② 从边的角度思考:AD:AB=AE:AC说明:本题是条件探究题。一般是由给定的结论反过来探究命题成立应具备的条件.已知正方形ABCD的边长是1,P是CD边的
中点,点Q在线段BC上,当Q在什么位置时,ΔADP与
以Q,C,P为顶点的三角形相似?尝试挑战②从ΔADP∽ΔPCQ的角度思考;分 析:
①从ΔADP∽ΔQCP的角度思考;再见
