相似三角形的识别3[下学期]
图片预览

文档简介
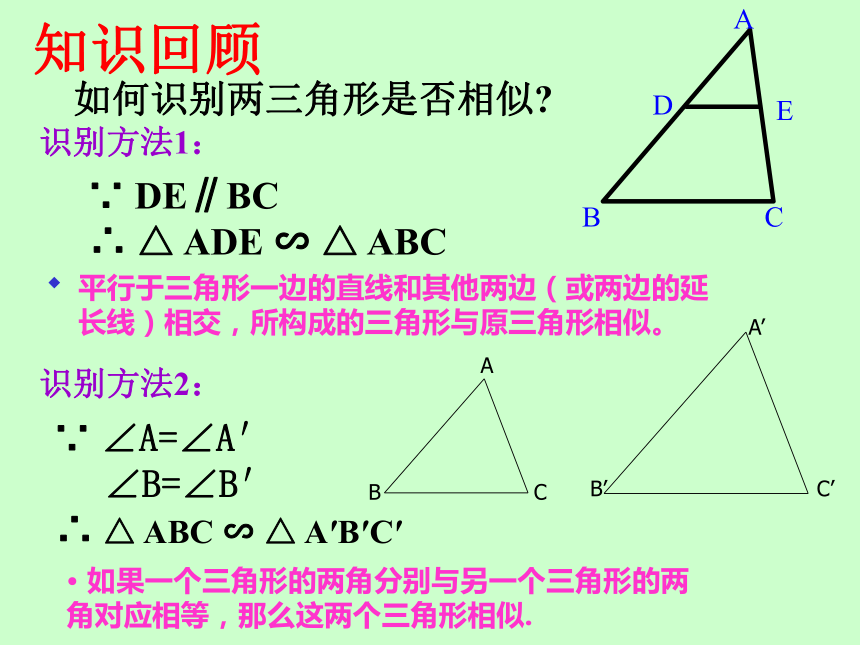
课件19张PPT。相似三角形的识别(3)如何识别两三角形是否相似?知识回顾 ∵ DE∥BC
∴ △ ADE ∽ △ ABC 识别方法1:识别方法2: ∵ ∠A=∠A′
∠B=∠B′
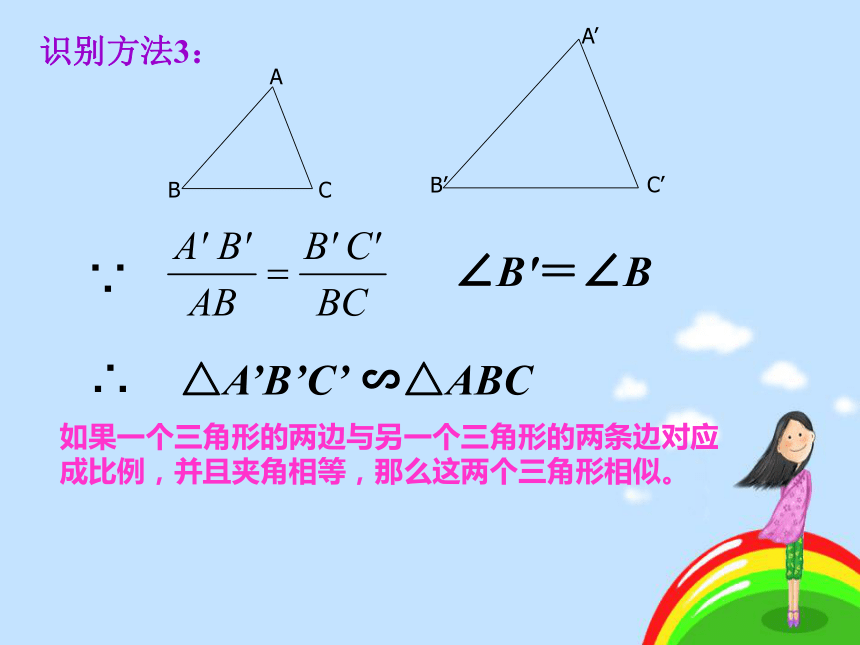
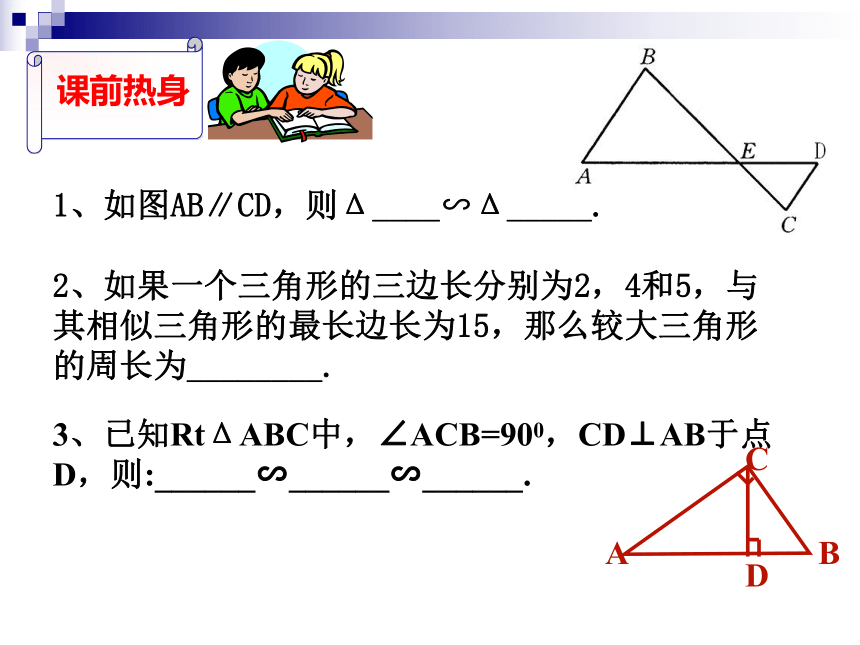
∴ △ ABC ∽ △ A′B′C′平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。 如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.如果一个三角形的两边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似。识别方法3:1、如图AB∥CD,则Δ____∽Δ_____.
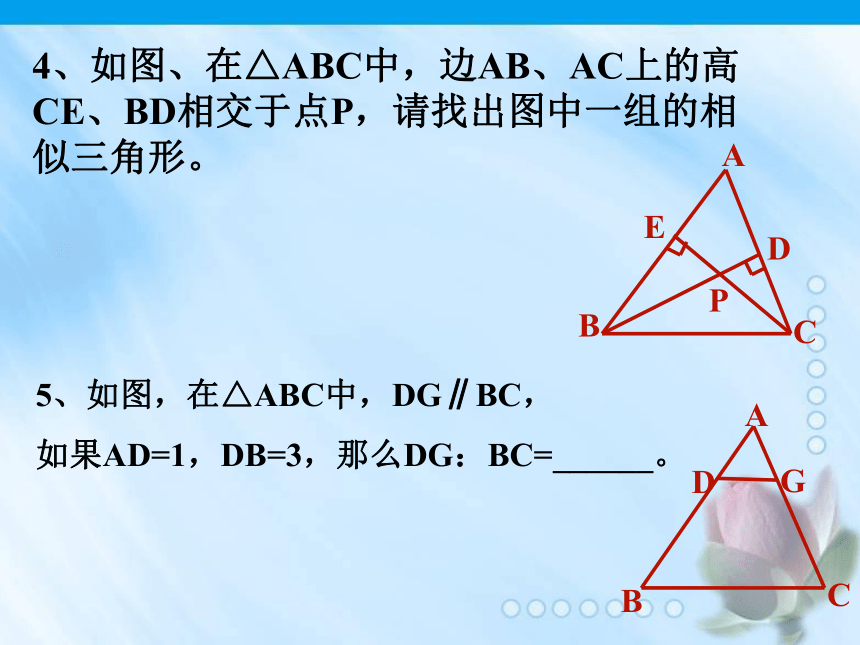
2、如果一个三角形的三边长分别为2,4和5,与其相似三角形的最长边长为15,那么较大三角形的周长为________.3、已知RtΔABC中,∠ACB=900,CD⊥AB于点D,则:______∽______∽______.4、如图、在△ABC中,边AB、AC上的高CE、BD相交于点P,请找出图中一组的相似三角形。5、如图,在△ABC中,DG∥BC,
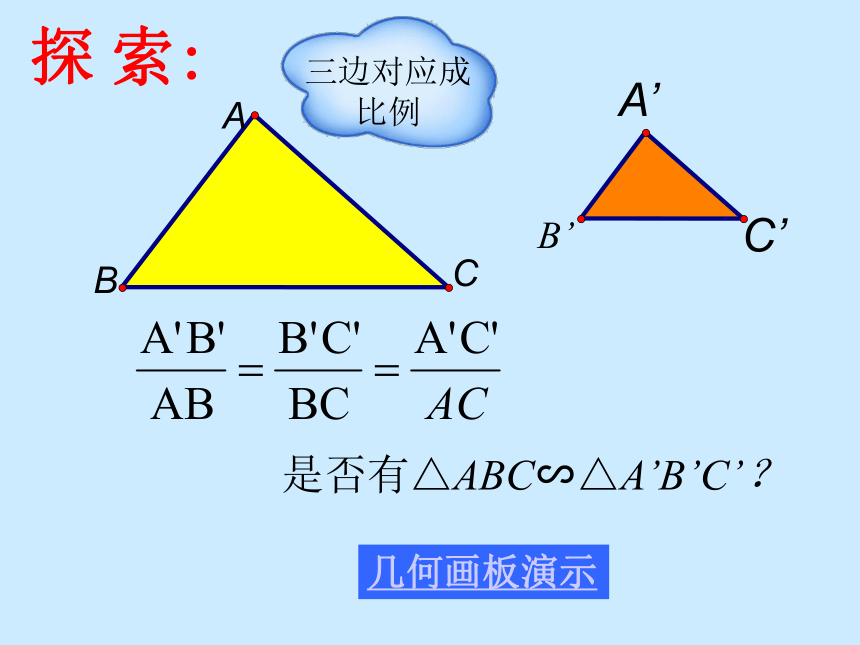
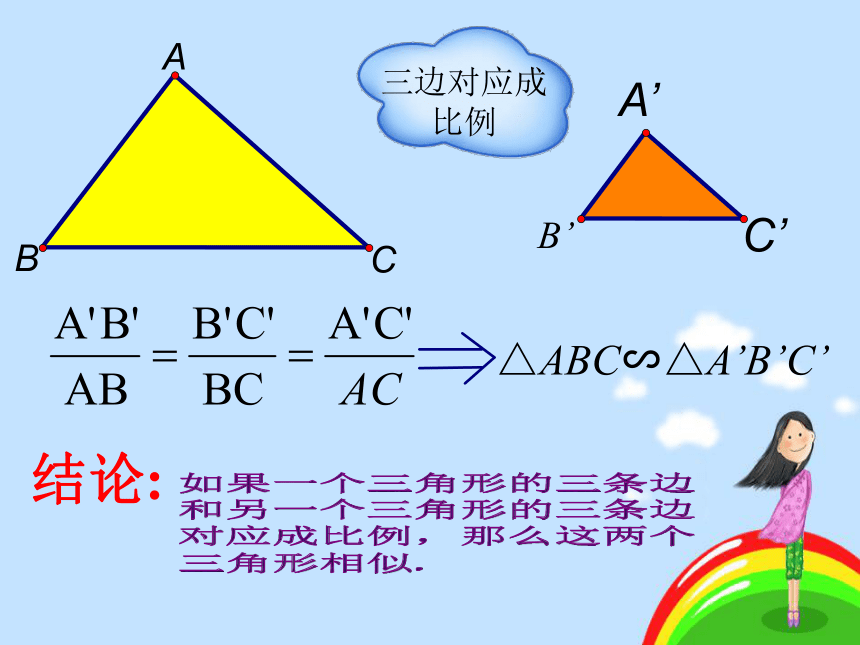
如果AD=1,DB=3,那么DG:BC=______。 是否有△ABC∽△A’B’C’?ABC三边对应成 比例几何画板演示探 索:如果一个三角形的三条边
和另一个三角形的三条边
对应成比例,那么这两个
三角形相似.ABC三边对应成 比例△ABC∽△A’B’C’结论:例1:在△ABC和△A′B′C′中,已知:AB=6 cm, BC=8 cm,AC=10 cm,A′B′=18 cm,B′C′=24 cm,A′C′=30 cm.试判定△ABC与A′B′C′是否相似,并说明理由. 新知运用两个等边三角形一定相似吗?问题:解:∵△ABC与△A’B’C’都是等边三角形 你来做做看吧!看已知条件识别相似选方法找出识别方法中所需的条件方法提炼体验成功试说明∠BAD=∠CAE.∴ΔABC∽ΔADE
∴∠BAC=∠DAE
∴∠BAC━∠DAC=∠DAE━∠DAC
即∠BAD=∠CAE 已知△ABC 中∠C=90°,D、E分别是AB、AC上的点且AD·AB= AE·AC
试说明:ED⊥AB你能再画一个与它们相似的三角形吗?
其相似比又是多少?答案是2:1探索展示自我如图,已知BD、CE为ABC的高,
试说明∠ADE=∠ABC.想一想自己来小结一下吧!小结两个三角形相似的识别方法:(1) 两角对应相等的两个三角形相似.
(2) 三边对应成比例的两个三角形相似.
(3) 两边对应成比例且夹角相等的两个 三角形相似.两边对应成比例且其中一边的对角对应相等的两个三角形是否相似呢?已知:△A’B’C’ ∽△ABC在△ABC中,以B为圆心,连结BD,则BD=BA.BA长为半径画弧,交AC于D,拓展
∴ △ ADE ∽ △ ABC 识别方法1:识别方法2: ∵ ∠A=∠A′
∠B=∠B′
∴ △ ABC ∽ △ A′B′C′平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。 如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.如果一个三角形的两边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似。识别方法3:1、如图AB∥CD,则Δ____∽Δ_____.
2、如果一个三角形的三边长分别为2,4和5,与其相似三角形的最长边长为15,那么较大三角形的周长为________.3、已知RtΔABC中,∠ACB=900,CD⊥AB于点D,则:______∽______∽______.4、如图、在△ABC中,边AB、AC上的高CE、BD相交于点P,请找出图中一组的相似三角形。5、如图,在△ABC中,DG∥BC,
如果AD=1,DB=3,那么DG:BC=______。 是否有△ABC∽△A’B’C’?ABC三边对应成 比例几何画板演示探 索:如果一个三角形的三条边
和另一个三角形的三条边
对应成比例,那么这两个
三角形相似.ABC三边对应成 比例△ABC∽△A’B’C’结论:例1:在△ABC和△A′B′C′中,已知:AB=6 cm, BC=8 cm,AC=10 cm,A′B′=18 cm,B′C′=24 cm,A′C′=30 cm.试判定△ABC与A′B′C′是否相似,并说明理由. 新知运用两个等边三角形一定相似吗?问题:解:∵△ABC与△A’B’C’都是等边三角形 你来做做看吧!看已知条件识别相似选方法找出识别方法中所需的条件方法提炼体验成功试说明∠BAD=∠CAE.∴ΔABC∽ΔADE
∴∠BAC=∠DAE
∴∠BAC━∠DAC=∠DAE━∠DAC
即∠BAD=∠CAE 已知△ABC 中∠C=90°,D、E分别是AB、AC上的点且AD·AB= AE·AC
试说明:ED⊥AB你能再画一个与它们相似的三角形吗?
其相似比又是多少?答案是2:1探索展示自我如图,已知BD、CE为ABC的高,
试说明∠ADE=∠ABC.想一想自己来小结一下吧!小结两个三角形相似的识别方法:(1) 两角对应相等的两个三角形相似.
(2) 三边对应成比例的两个三角形相似.
(3) 两边对应成比例且夹角相等的两个 三角形相似.两边对应成比例且其中一边的对角对应相等的两个三角形是否相似呢?已知:△A’B’C’ ∽△ABC在△ABC中,以B为圆心,连结BD,则BD=BA.BA长为半径画弧,交AC于D,拓展
