相似三角形的识别2[下学期]

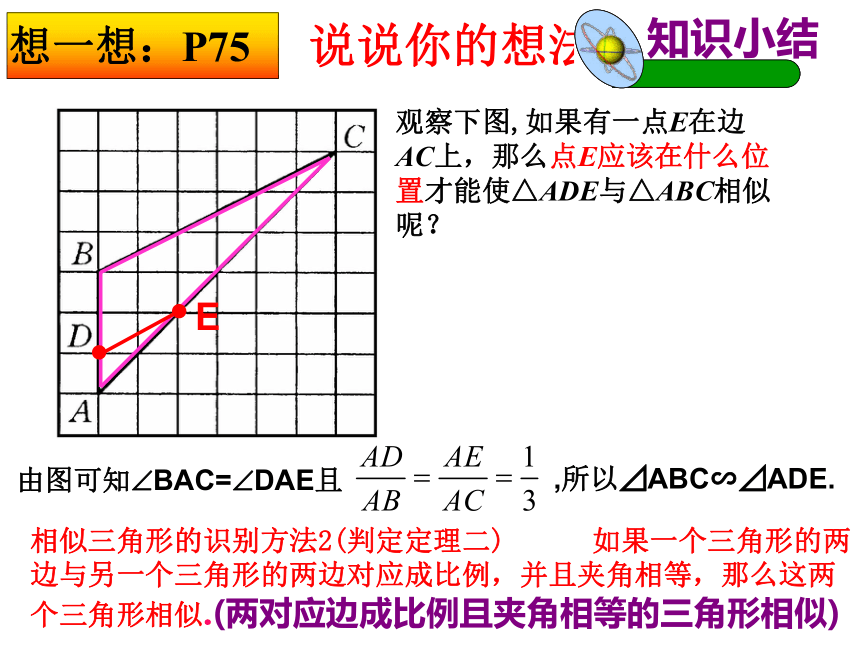
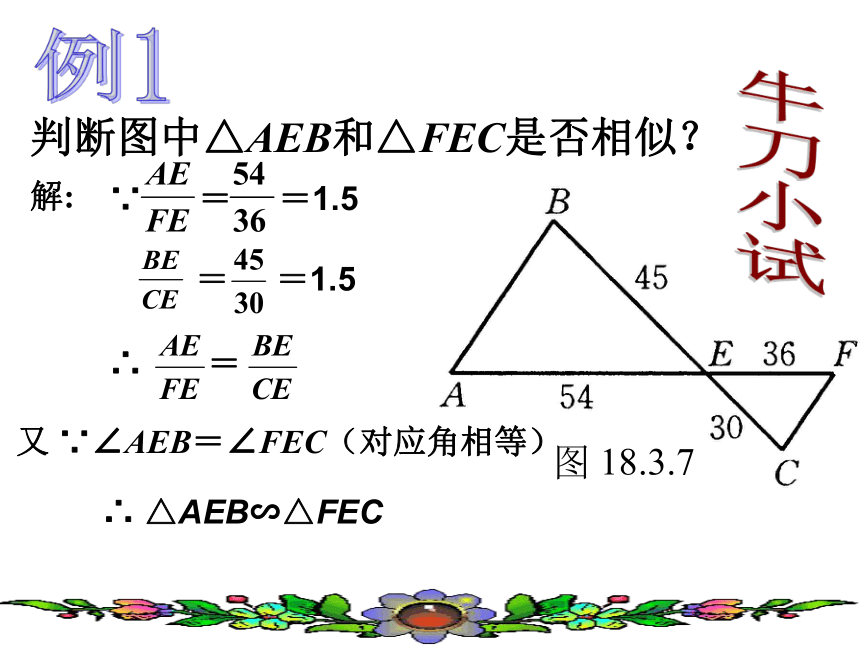
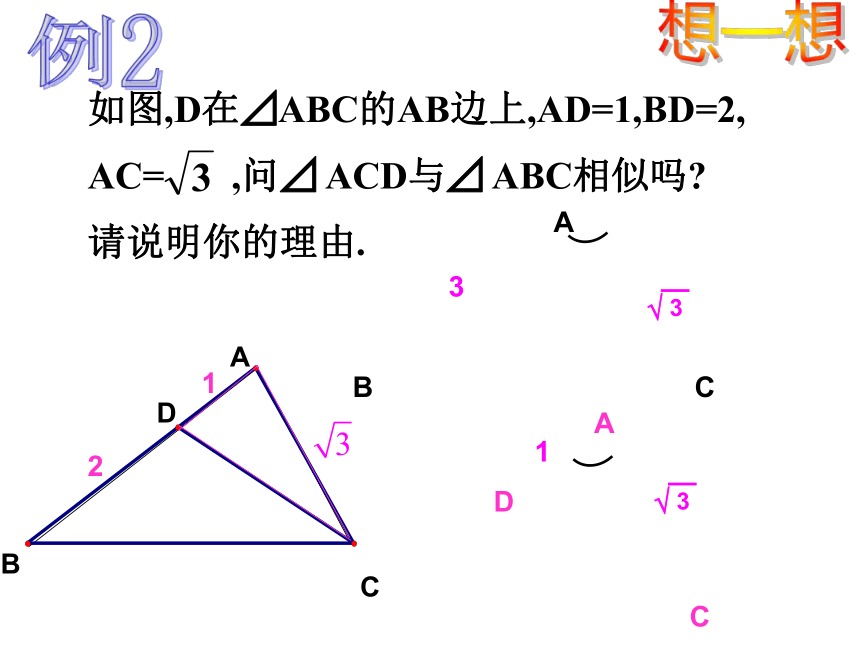
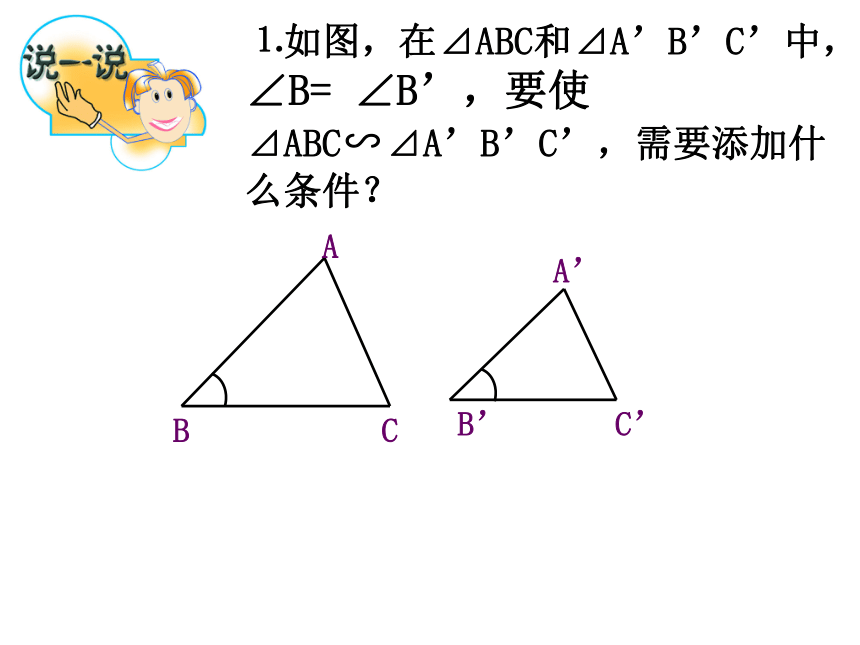
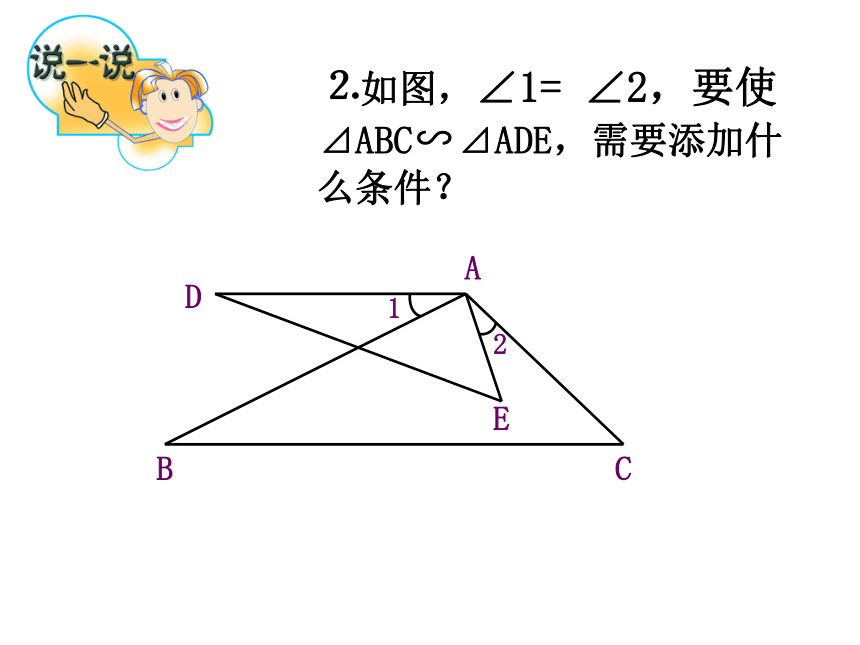
课件13张PPT。相似三角形的识别(2)想一想：P75观察下图,如果有一点E在边AC上，那么点E应该在什么位置才能使△ADE与△ABC相似呢？ E说说你的想法相似三角形的识别方法2(判定定理二) 如果一个三角形的两边与另一个三角形的两边对应成比例，并且夹角相等，那么这两个三角形相似.(两对应边成比例且夹角相等的三角形相似)由图可知?BAC=?DAE且,所以⊿ABC∽⊿ADE.判断图中△AEB和△FEC是否相似？ 解: 牛刀小试例1∴ △AEB∽△FEC 又 ∵∠AEB＝∠FEC（对应角相等） 想一想例2DAC31⒈如图，在⊿ABC和⊿A’B’C’中，∠B= ∠B’，要使⊿ABC∽⊿A’B’C’，需要添加什么条件？⒉如图，∠1= ∠2，要使⊿ABC∽⊿ADE，需要添加什么条件？⒊如图，要使⊿ABC∽⊿ACD，需要添加什么条件？⒋如图，将方格纸分成6个三角形，在②-⑥5个三角形中，与三角形①相似的有哪些？为什么？112⒌如图，在⊿ABC中，AB=4，AC=2.
⑴在AB上取一点D，当AD=_______时， ⊿ACD∽ ⊿ABC？
⑵在AC的延长线上取一点E，当CE=_____ 时， ⊿AEB∽⊿ABC？
⑶此时BE与DC的位置关系怎样？为什么？ABC42E61 如图,某陶瓷厂的质量检查员准备检测花瓶内径,但用直尺无法直接测量。
1、你能想出什么办法可以测量花瓶的内径吗？2、检查员用一个交叉卡钳去量，已知OA：OC
=OB：OD=1:2，且量得CD=12cm，你能说出内径AB的长度是多少？为什么?分析：若△AOB∽△COD，则AB：CD=OA：OC=1:2，从而就可以求出AB=6cm。问题是：能否从已知条件得到△AOB∽△COD?
请同学们思考一下.两边对应成比例且其中一边的对角对应相等的两个三角形是否相似呢？已知：△A’B’C’ ∽△ABC在△ABC中，以B为圆心，连结BD，则BD＝BA.BA长为半径画弧，交AC于D，ADBC这节课我们学了什么？ 识别相似三角形的方法有哪些？1、如果一个三角形的两角分别与另一个三角形的两角对应相等，那么这两个三角形相似。2、如果一个三角形的两条边与另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似． 你已经掌握了哪些识别相似三角形的法？3、判定定理一:如果一个三角形的两角分别与另一个三角形的两角对应相等，那么这两个三角形相似。(两组对应角相等的三角形相似 )4、判定定理二:如果一个三角形的两条边与另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似．(两对应边成比例且夹角相等的三角形相似)1 、相似三角形的定义:对应角相等,对应边
成比例的两个三角形相似.2 、相似三角形的预备定理:平行于三角形一边的直线与其它两边(或其延长线)相交,所得的三角形与原三角形相似.