相似三角形的识别[下学期]
图片预览




文档简介
课件18张PPT。 相似三角形的
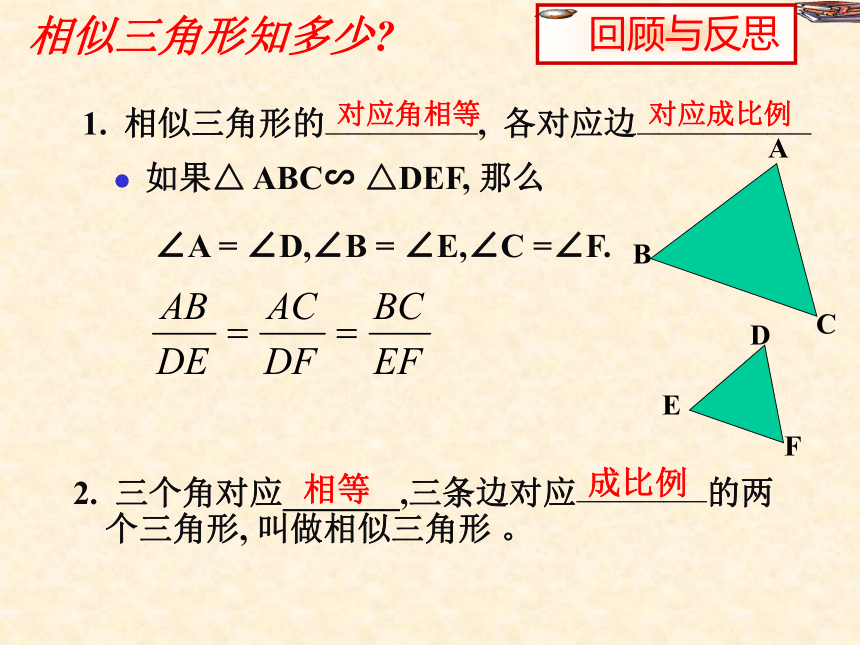
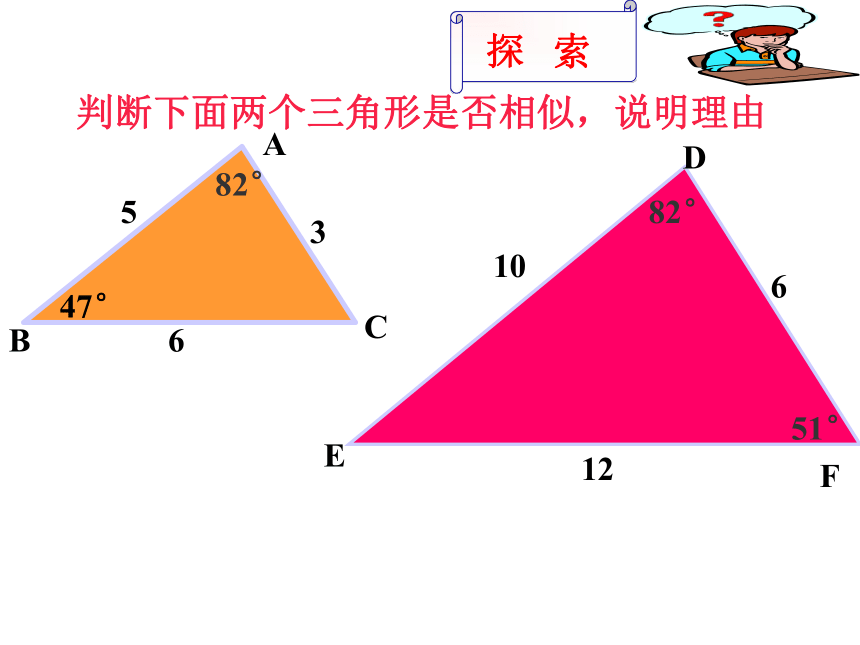
识别(一) 丰惠镇中 葛建萍相似三角形知多少?2. 三个角对应_______,三条边对应——————的两个三角形, 叫做相似三角形 。相等成比例对应角相等对应成比例 如果△ ABC∽ △DEF, 那么1. 相似三角形的———————, 各对应边————————ABCDEF∠A = ∠D,∠B = ∠E,∠C =∠F.判断下面两个三角形是否相似,说明理由 ABCDE F 5361061282°47°82°51°探 索 探 索画△ABC,使得∠A=60°∠B=45°∠C=75°画一画:识别三角形相似的方法之一如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似。(简称为:两角对应相等,两三角形相似)如图,在△ ABC和△ DEF中
如果∠A=∠D, ∠B=∠E.
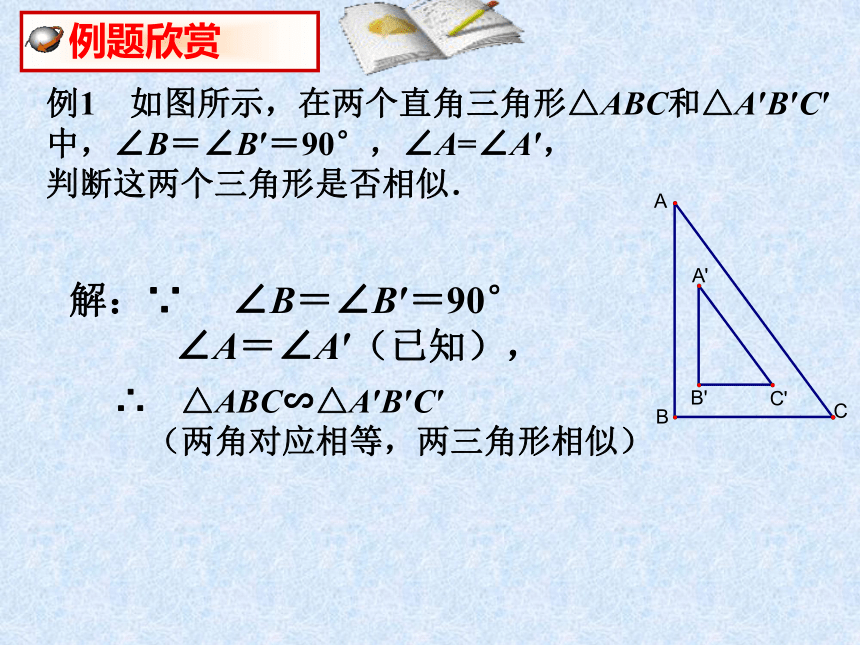
那么△ ABC∽ △DEF讨论:只有一对角对应相等的两个三角形相似吗?例1 如图所示,在两个直角三角形△ABC和△A′B′C′中,∠B=∠B′=90°,∠A=∠A′,
判断这两个三角形是否相似. 解:∵ ∠B=∠B′=90°
∠A=∠A′(已知),
∴ △ABC∽△A′B′C′
(两角对应相等,两三角形相似)(1)DE∥BC△ ∽△ . ADE ACB(2)DE∥BC提升能力的奥秘ADE ABC△ ∽△ . AEDBCABCDE根据给出的条件,按相应顺序写出 相似三角形并说明理由 例2 如图,△ABC中,DE∥BC,解: ∵ DE∥BC,EF∥AB
∴ ∠A=∠FEC ∠AED=∠C
(两直线平行,同位角相等)
F思考(1)如果点D恰好是边AB的中点,则点E是边AC的中点吗?ACDEBEF∥AB, 试说明△ADE∽△EFC.(2) DE和BC又有什么关系呢? ∴ △ADE∽△EFC.
(两角对应相等,两个三角形相似.)(3)∠1=∠B (4)∠B=∠C △ ∽△ . CADB1ADCEBABD ACEABC ACD△ ∽ △ . 提升能力的奥秘(5)∠1=∠2
∠E=∠CB
C
E
D
2△ ∽ △ . ADE ABCA(6)直角△ABC中,∠ACB=900,
CD⊥AB垂足为D 则 ABC ACD CBD△——∽ △——∽ △——提升能力的奥秘 一般的,对顶角、公共角、同角的余角(或补角),平行线所成的同位角、内错角都是相等的,是说明两个三角形相似的重要依据。学习小结判断:
(1)有一个锐角相等的两个直角三角形相似 ( )
(2)有一个角等于1000的两个等腰三角形相似 ( )
(3)有一个角等于600的两个等腰三角形相似 ( )
(4)有一个角等于300的两个等腰三角形相似 ( )
(5)有一个角相等的两个等腰三角形相似 ( )×√√√×我练我进步1、图中DG∥EH∥FI∥BC,
找出图中所有的相似三角形 △ADG∽ △AEH ∽ △AFI ∽ △ABC我练我进步2、△ABE∽△ACD△BOD ∽△COE我练我进步 挑战自我如图,在△ABC中,点D为AC边上一点,
过点D画直线截△ABC,使截得的三角形与
原三角形相似,你能画出这样的直线吗?
能画出几条?ABC·D回味无穷判定三角形相似的常用方法:如图,在△ ABC和△DEF中
如果∠A=∠D, ∠B=∠E,
那么△ ABC∽ △DEF.两角对应相等的两个三角形相似.常见图形:Thank you!
识别(一) 丰惠镇中 葛建萍相似三角形知多少?2. 三个角对应_______,三条边对应——————的两个三角形, 叫做相似三角形 。相等成比例对应角相等对应成比例 如果△ ABC∽ △DEF, 那么1. 相似三角形的———————, 各对应边————————ABCDEF∠A = ∠D,∠B = ∠E,∠C =∠F.判断下面两个三角形是否相似,说明理由 ABCDE F 5361061282°47°82°51°探 索 探 索画△ABC,使得∠A=60°∠B=45°∠C=75°画一画:识别三角形相似的方法之一如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似。(简称为:两角对应相等,两三角形相似)如图,在△ ABC和△ DEF中
如果∠A=∠D, ∠B=∠E.
那么△ ABC∽ △DEF讨论:只有一对角对应相等的两个三角形相似吗?例1 如图所示,在两个直角三角形△ABC和△A′B′C′中,∠B=∠B′=90°,∠A=∠A′,
判断这两个三角形是否相似. 解:∵ ∠B=∠B′=90°
∠A=∠A′(已知),
∴ △ABC∽△A′B′C′
(两角对应相等,两三角形相似)(1)DE∥BC△ ∽△ . ADE ACB(2)DE∥BC提升能力的奥秘ADE ABC△ ∽△ . AEDBCABCDE根据给出的条件,按相应顺序写出 相似三角形并说明理由 例2 如图,△ABC中,DE∥BC,解: ∵ DE∥BC,EF∥AB
∴ ∠A=∠FEC ∠AED=∠C
(两直线平行,同位角相等)
F思考(1)如果点D恰好是边AB的中点,则点E是边AC的中点吗?ACDEBEF∥AB, 试说明△ADE∽△EFC.(2) DE和BC又有什么关系呢? ∴ △ADE∽△EFC.
(两角对应相等,两个三角形相似.)(3)∠1=∠B (4)∠B=∠C △ ∽△ . CADB1ADCEBABD ACEABC ACD△ ∽ △ . 提升能力的奥秘(5)∠1=∠2
∠E=∠CB
C
E
D
2△ ∽ △ . ADE ABCA(6)直角△ABC中,∠ACB=900,
CD⊥AB垂足为D 则 ABC ACD CBD△——∽ △——∽ △——提升能力的奥秘 一般的,对顶角、公共角、同角的余角(或补角),平行线所成的同位角、内错角都是相等的,是说明两个三角形相似的重要依据。学习小结判断:
(1)有一个锐角相等的两个直角三角形相似 ( )
(2)有一个角等于1000的两个等腰三角形相似 ( )
(3)有一个角等于600的两个等腰三角形相似 ( )
(4)有一个角等于300的两个等腰三角形相似 ( )
(5)有一个角相等的两个等腰三角形相似 ( )×√√√×我练我进步1、图中DG∥EH∥FI∥BC,
找出图中所有的相似三角形 △ADG∽ △AEH ∽ △AFI ∽ △ABC我练我进步2、△ABE∽△ACD△BOD ∽△COE我练我进步 挑战自我如图,在△ABC中,点D为AC边上一点,
过点D画直线截△ABC,使截得的三角形与
原三角形相似,你能画出这样的直线吗?
能画出几条?ABC·D回味无穷判定三角形相似的常用方法:如图,在△ ABC和△DEF中
如果∠A=∠D, ∠B=∠E,
那么△ ABC∽ △DEF.两角对应相等的两个三角形相似.常见图形:Thank you!
