相似三角形的识别[下学期]
图片预览
文档简介
相似三角形的识别
一、教学目标:
1. 知识目标:探索并掌握“两角对应相等的两个三角形相似”的识别方法。
2. 能力目标:培养学生动手操作的习惯和观察问题的能力,发展合情推理能力。
教学重点:
探索“两角对应相等的两个三角形相似”,以及这个识别方法的简单应用。
教学难点:
会应用识别的方法,有条理地说理。
二、教学过程:
(1) 新知准备
1. 两个三角形相似,必须符合什么条件?(回忆定义)
2. 课本第72页“做一做”:请同学们通过度量,判断△ABC与△ADE是否相似?
(请一位同学说出是如何判断的,补充完整)
3. 作△ADE关于点A的中心对称图形,得到△AD/E/,△AD/E/与△ABC还相似吗?为什么?(利用旋转的性质和第2问的结果)
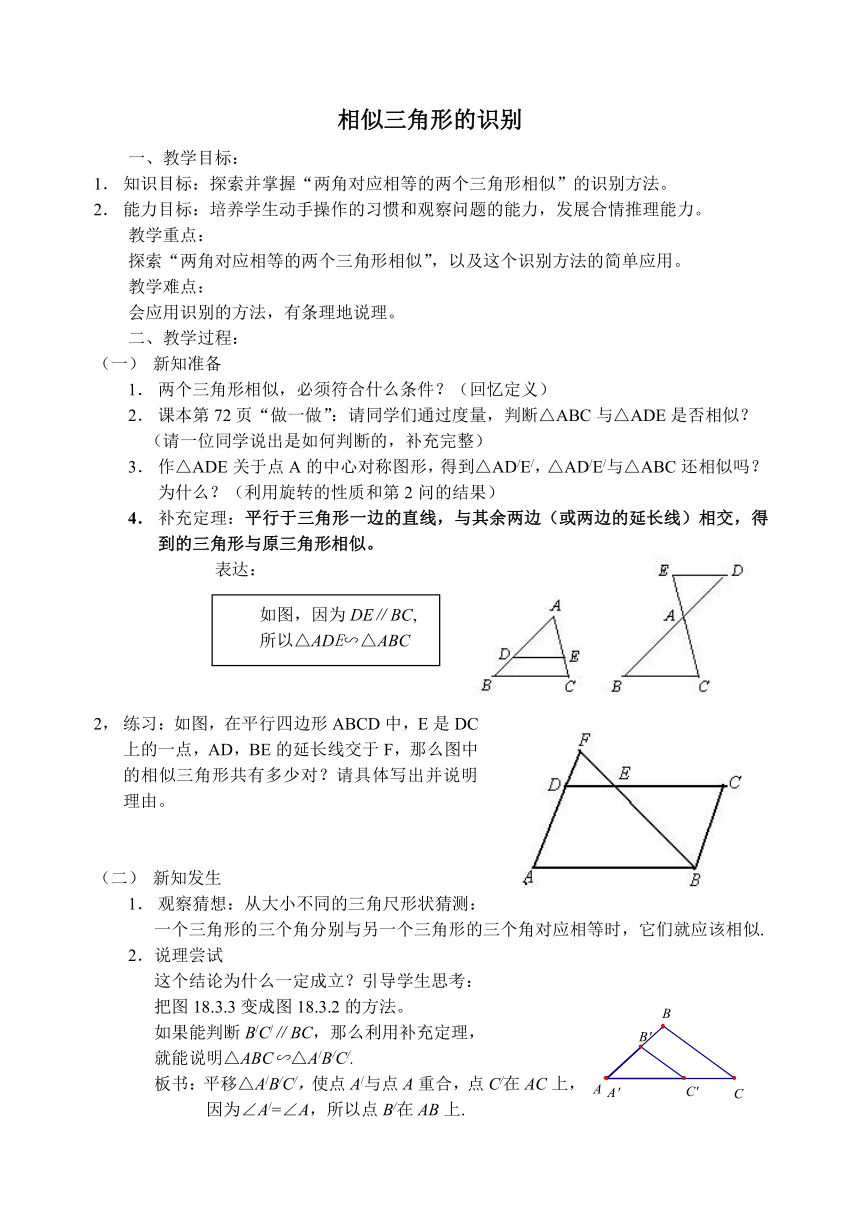
4. 补充定理:平行于三角形一边的直线,与其余两边(或两边的延长线)相交,得到的三角形与原三角形相似。
表达:
2, 练习:如图,在平行四边形ABCD中,E是DC上的一点,AD,BE的延长线交于F,那么图中的相似三角形共有多少对?请具体写出并说明理由。
(2) 新知发生
1. 观察猜想:从大小不同的三角尺形状猜测:
一个三角形的三个角分别与另一个三角形的三个角对应相等时,它们就应该相似.
2.说理尝试
这个结论为什么一定成立?引导学生思考:
把图18.3.3变成图18.3.2的方法。
如果能判断B/C/∥BC,那么利用补充定理,
就能说明△ABC∽△A/B/C/.
板书:平移△A/B/C/,使点A/与点A重合,点C/在AC上,
因为∠A/=∠A,所以点B/在AB上.
又因为∠A/C/ B/=∠C,所以B/C/∥BC,
根据补充定理,△ABC∽△A/B/C/.
3.识别方法的最后概括
三对角对应相等,条件是否太多了?
结论:如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似。
(3) 应用举例:
例1 如图18.3.5,△ABC中,DE∥BC,EF∥AB,
试说明△ADE∽△EFC.
学生口述,老师示范
解 因为DE∥BC,EF∥AB(已知),
所以∠ADE=∠B,∠EFC=∠B,(两直线平行,同位角相等), 所以 ∠ADE=∠EFC(等量代换)
又因为 ∠AED=∠C,(两直线平行,同位角相等)
所以 △ADE∽△EFC. (识别方法1)
练习检验
1. 如图CD是直角三角形ABC斜边上的高,请说明
△ACD∽△CBD.
。.
(4) 课堂练习:
1.如图,B、D、E在同一直线上,且,又,试判断△ABC和△ADE是否相似,并说明理由。
(5) 小结:
识别两个三角形相似的两个方法:
1. 平行线截三角形得到的三角形与原三角形相似,如图。
2. 说明2个三角形相似只要说明它们2 对角对应相等。
要求有规范的书写格式。
如图,因为DE∥BC,
所以△ADE∽△ABC
一、教学目标:
1. 知识目标:探索并掌握“两角对应相等的两个三角形相似”的识别方法。
2. 能力目标:培养学生动手操作的习惯和观察问题的能力,发展合情推理能力。
教学重点:
探索“两角对应相等的两个三角形相似”,以及这个识别方法的简单应用。
教学难点:
会应用识别的方法,有条理地说理。
二、教学过程:
(1) 新知准备
1. 两个三角形相似,必须符合什么条件?(回忆定义)
2. 课本第72页“做一做”:请同学们通过度量,判断△ABC与△ADE是否相似?
(请一位同学说出是如何判断的,补充完整)
3. 作△ADE关于点A的中心对称图形,得到△AD/E/,△AD/E/与△ABC还相似吗?为什么?(利用旋转的性质和第2问的结果)
4. 补充定理:平行于三角形一边的直线,与其余两边(或两边的延长线)相交,得到的三角形与原三角形相似。
表达:
2, 练习:如图,在平行四边形ABCD中,E是DC上的一点,AD,BE的延长线交于F,那么图中的相似三角形共有多少对?请具体写出并说明理由。
(2) 新知发生
1. 观察猜想:从大小不同的三角尺形状猜测:
一个三角形的三个角分别与另一个三角形的三个角对应相等时,它们就应该相似.
2.说理尝试
这个结论为什么一定成立?引导学生思考:
把图18.3.3变成图18.3.2的方法。
如果能判断B/C/∥BC,那么利用补充定理,
就能说明△ABC∽△A/B/C/.
板书:平移△A/B/C/,使点A/与点A重合,点C/在AC上,
因为∠A/=∠A,所以点B/在AB上.
又因为∠A/C/ B/=∠C,所以B/C/∥BC,
根据补充定理,△ABC∽△A/B/C/.
3.识别方法的最后概括
三对角对应相等,条件是否太多了?
结论:如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似。
(3) 应用举例:
例1 如图18.3.5,△ABC中,DE∥BC,EF∥AB,
试说明△ADE∽△EFC.
学生口述,老师示范
解 因为DE∥BC,EF∥AB(已知),
所以∠ADE=∠B,∠EFC=∠B,(两直线平行,同位角相等), 所以 ∠ADE=∠EFC(等量代换)
又因为 ∠AED=∠C,(两直线平行,同位角相等)
所以 △ADE∽△EFC. (识别方法1)
练习检验
1. 如图CD是直角三角形ABC斜边上的高,请说明
△ACD∽△CBD.
。.
(4) 课堂练习:
1.如图,B、D、E在同一直线上,且,又,试判断△ABC和△ADE是否相似,并说明理由。
(5) 小结:
识别两个三角形相似的两个方法:
1. 平行线截三角形得到的三角形与原三角形相似,如图。
2. 说明2个三角形相似只要说明它们2 对角对应相等。
要求有规范的书写格式。
如图,因为DE∥BC,
所以△ADE∽△ABC
