相似三角形的识别(一)[下学期]
图片预览





文档简介
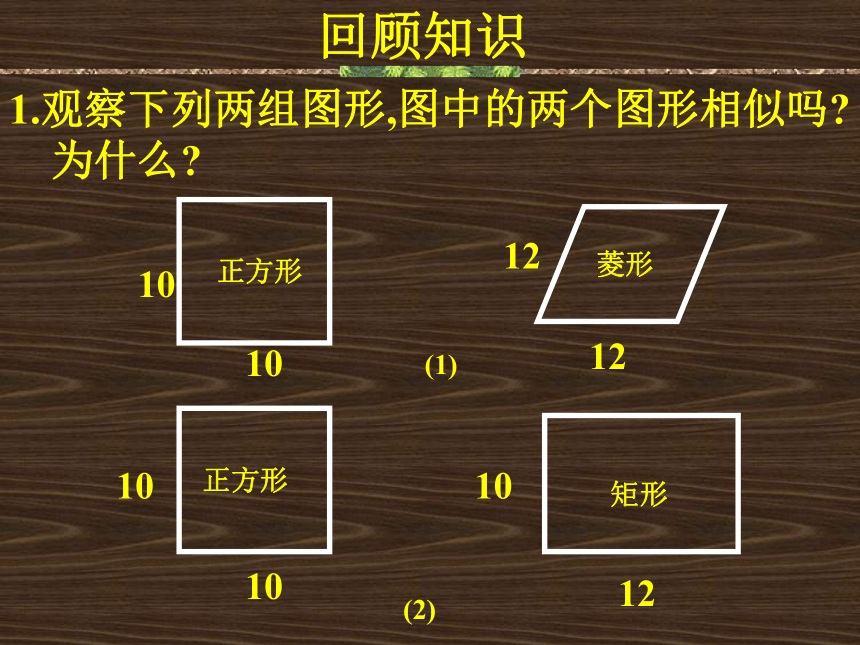
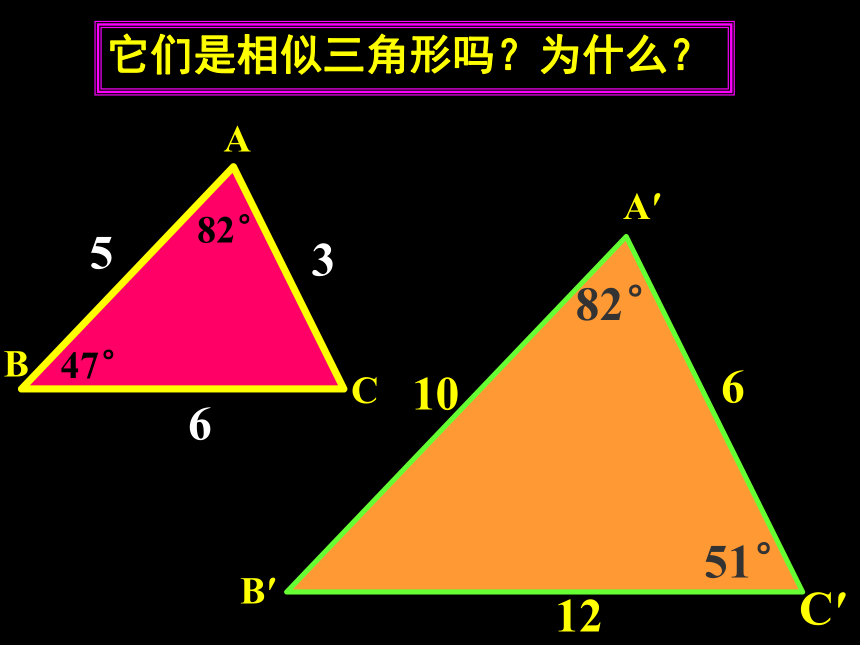
课件19张PPT。相似三角形的识别1.观察下列两组图形,图中的两个图形相似吗?为什么?10101212(1)正方形菱形正方形矩形10101012(2)回顾知识相似多边形的特征:对应边成比例,对应角相等。 三个角对应相等,三条边对应成比例的两个三角形, 做相似三角形相似三角形的特征:2.已知△ABC ∽ △ADE,其中∠ADE= ∠B, ∠DAE = ∠BAC.,找出图中相似三角形的对应边。回顾知识A′B′C′A1061251°82°它们是相似三角形吗?为什么?6这两个三角形的三个内角的大小有什么关系?三个内角对应相等的两个三角形一定相似吗?三个内角对应相等。思考相
似如果一个三角形的三个角分别与另一个三角形的三个角对应相等,那么这两个三角形_______.
根据三角形内角和定理,我们知道如果两个三角形有两对角对应相等,那么第三对角也一定对应相等.
相似思 考
如果两个三角形仅有一对角是对应相等的,那么它们是否一定相似?
如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.相似三角形的识别方法:CC'∵ ∠A=∠A', ∠B=∠B'∴ ΔABC ∽ ΔA'B'C'用数学符号表示:相似三角形的识别在两个直角三角形△ABC和△A′B′C′中, ∠B=∠B′=90°,∠A=∠A′,判断这两个三角形是否相似. 解:∵ ∠B=∠B′=90°∠A=∠A′∴△ABC∽△A′B′C′1、利用前面所学的知识你能判断下面那些是相似三角形吗?①A与B相似②D与E相似40°65°A40°75°B80°CD65°45°70°E45°75°70°1. 根据给出的条件,按相应顺序写出 相似三角形并说明理由(要求步步有依据)(2)DE∥BC
△_____∽ △_____△ ∽ △ . (1)DE∥BC ADE ABCADE ACB例2. 如图18.3.5,△ABC中,
DE∥BC,EF∥AB,
试说明△ADE∽△EFC. 解: ∵ DE∥BC,EF∥AB∴ ∠1=∠B=∠2∠3=∠C. ∴ △ADE∽△EFC. 123 △ABC 中,DE∥BC,GF∥AB,DE、GF交于点O,则图中与△ABC相似的三角形共有多少个?请你写出来.解: 与△ABC相似的三角形有3个:
△ADE △GFC △GOE∴ △ ABC ∽ △ ADE 又∵ ∠B = ∠ADE解:∵ ∠1= ∠2∴ ∠1+ ∠3= ∠2+ ∠3即 ∠BAC= ∠DAE3如图,在Rt△ABC的一边AB上有一点P(点P与点A,B不重合),过点P作直线截得的三角形与△ABC相似,想一想满足条件的直线共有多少条?试画出图形并简要说明理由.相似三角形的识别方法有那些?方法1:通过定义方法2:通过两角对应相等。课 堂 小 结(这可是今天新学的,要牢记噢!)
似如果一个三角形的三个角分别与另一个三角形的三个角对应相等,那么这两个三角形_______.
根据三角形内角和定理,我们知道如果两个三角形有两对角对应相等,那么第三对角也一定对应相等.
相似思 考
如果两个三角形仅有一对角是对应相等的,那么它们是否一定相似?
如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.相似三角形的识别方法:CC'∵ ∠A=∠A', ∠B=∠B'∴ ΔABC ∽ ΔA'B'C'用数学符号表示:相似三角形的识别在两个直角三角形△ABC和△A′B′C′中, ∠B=∠B′=90°,∠A=∠A′,判断这两个三角形是否相似. 解:∵ ∠B=∠B′=90°∠A=∠A′∴△ABC∽△A′B′C′1、利用前面所学的知识你能判断下面那些是相似三角形吗?①A与B相似②D与E相似40°65°A40°75°B80°CD65°45°70°E45°75°70°1. 根据给出的条件,按相应顺序写出 相似三角形并说明理由(要求步步有依据)(2)DE∥BC
△_____∽ △_____△ ∽ △ . (1)DE∥BC ADE ABCADE ACB例2. 如图18.3.5,△ABC中,
DE∥BC,EF∥AB,
试说明△ADE∽△EFC. 解: ∵ DE∥BC,EF∥AB∴ ∠1=∠B=∠2∠3=∠C. ∴ △ADE∽△EFC. 123 △ABC 中,DE∥BC,GF∥AB,DE、GF交于点O,则图中与△ABC相似的三角形共有多少个?请你写出来.解: 与△ABC相似的三角形有3个:
△ADE △GFC △GOE∴ △ ABC ∽ △ ADE 又∵ ∠B = ∠ADE解:∵ ∠1= ∠2∴ ∠1+ ∠3= ∠2+ ∠3即 ∠BAC= ∠DAE3如图,在Rt△ABC的一边AB上有一点P(点P与点A,B不重合),过点P作直线截得的三角形与△ABC相似,想一想满足条件的直线共有多少条?试画出图形并简要说明理由.相似三角形的识别方法有那些?方法1:通过定义方法2:通过两角对应相等。课 堂 小 结(这可是今天新学的,要牢记噢!)
