图形的变换[下学期]
图片预览




文档简介
课件38张PPT。我们的世界"变换"多端,
把握住这种"变换",
也就把握住未来.南京外国语学校 苏竹青mathmath它们是怎么变过来的?mathmath1、图形的变换我们学习了哪几种形式? 平移、旋转、轴对称不变是图形的形状和大小,
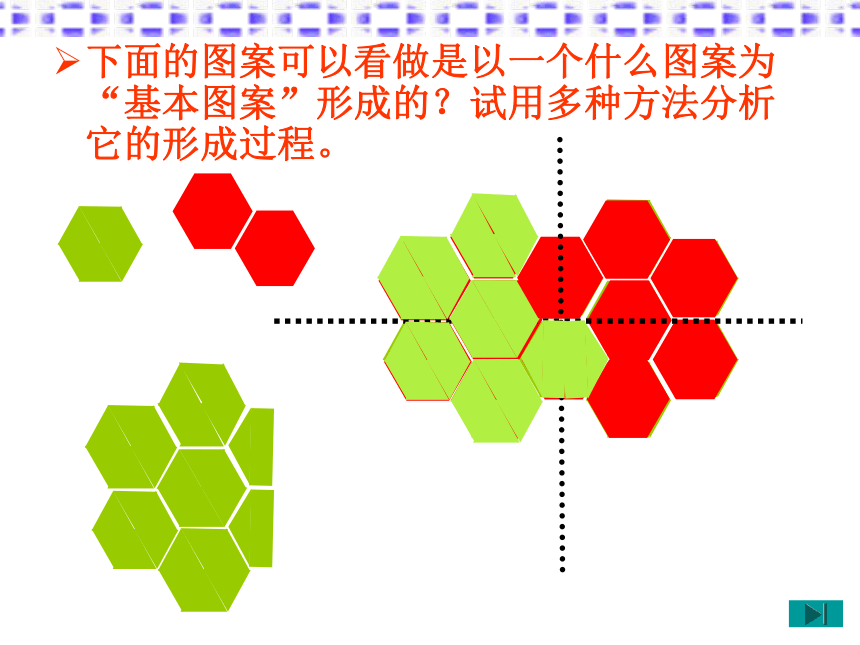
改变的是图形的位置.2、在变换过程中有哪些不变?哪些改变了?下面的图案可以看做是以一个什么图案为“基本图案”形成的?试用多种方法分析它的形成过程。
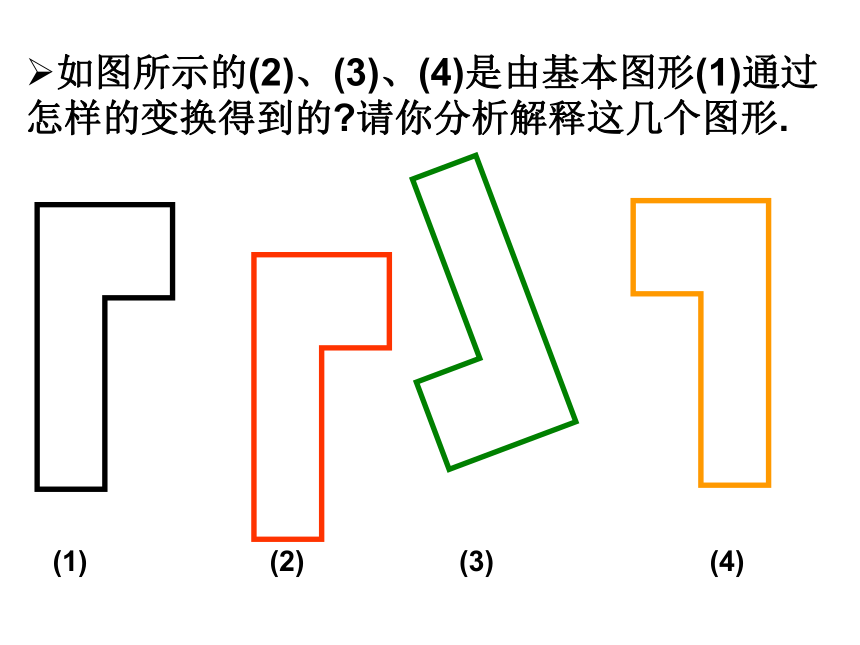
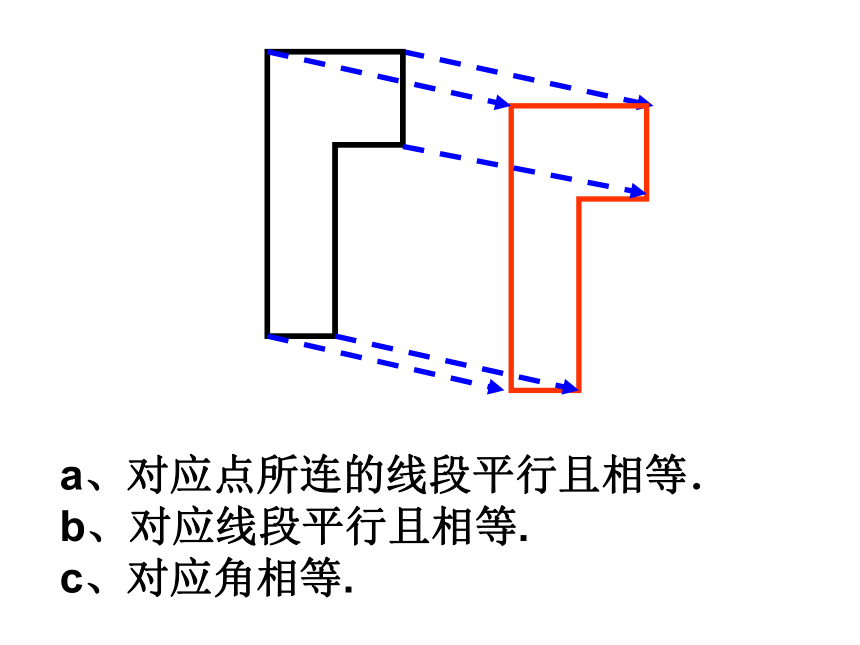
如图所示的(2)、(3)、(4)是由基本图形(1)通过怎样的变换得到的?请你分析解释这几个图形.(1)(2)(3)(4)a、对应点所连的线段平行且相等.
b、对应线段平行且相等.
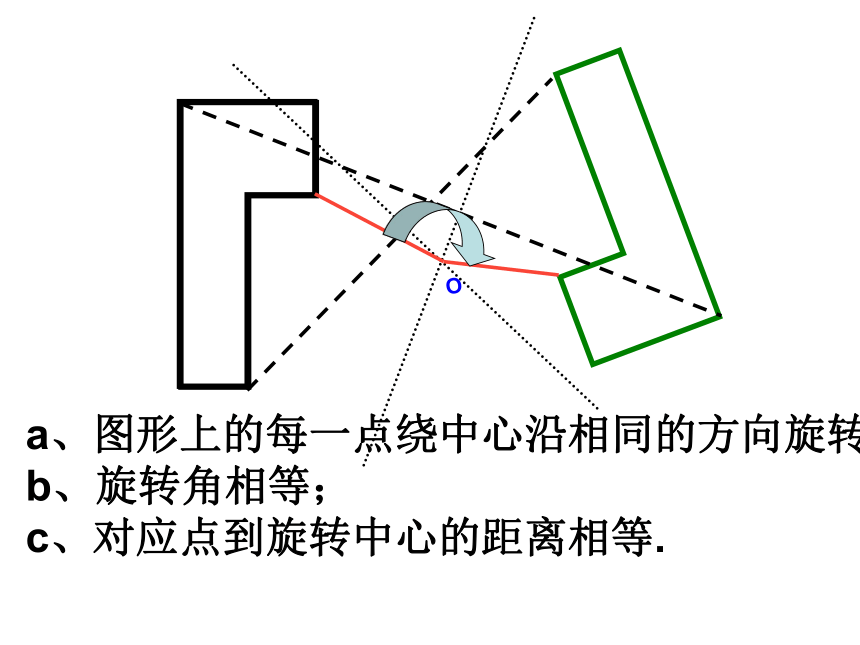
c、对应角相等.Oa、图形上的每一点绕中心沿相同的方向旋转
b、旋转角相等;
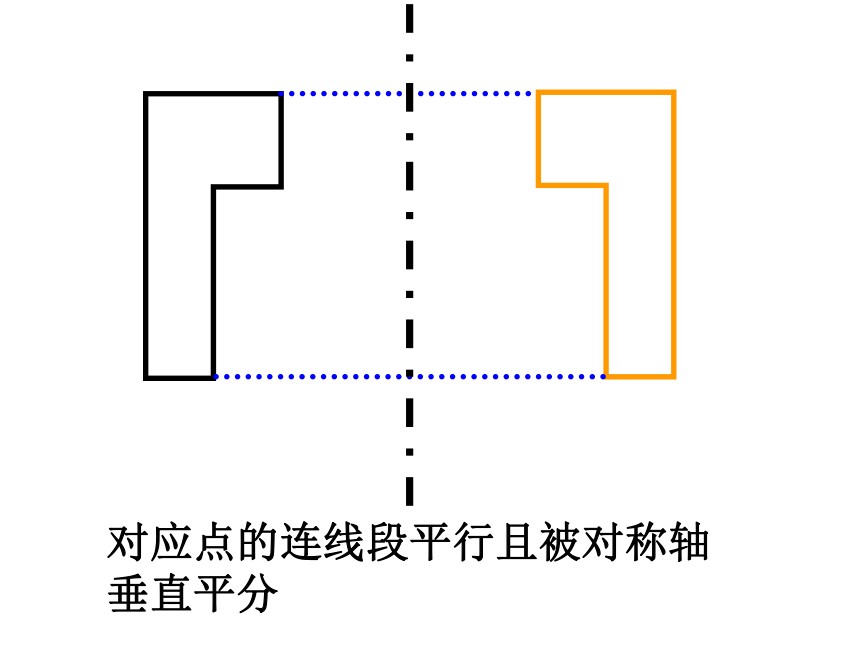
c、对应点到旋转中心的距离相等.对应点的连线段平行且被对称轴垂直平分1、平移变换:我们如何确定它的2、旋转变换:我们如何确定它的3、轴对称变换:我们如何确定它的方向与距离旋转中心与
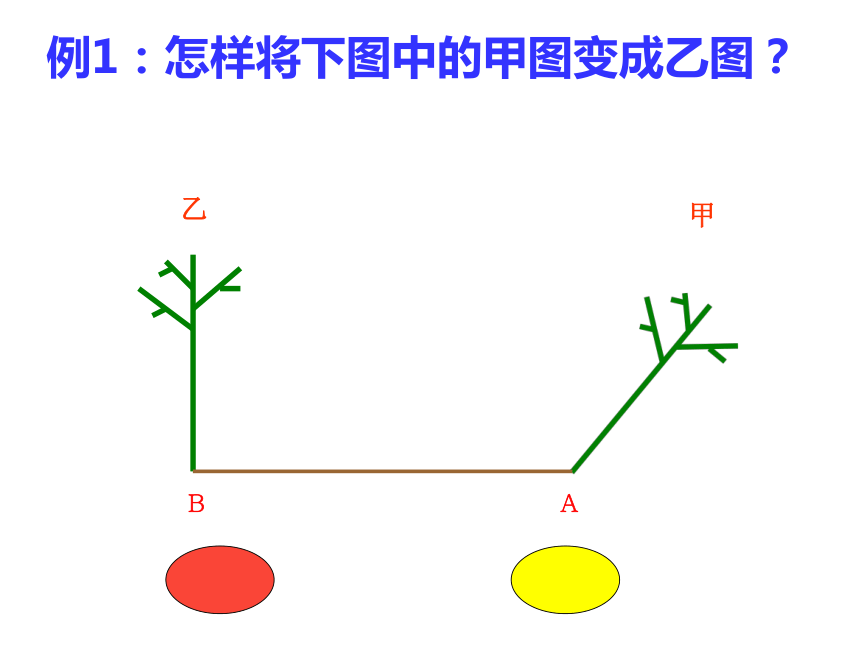
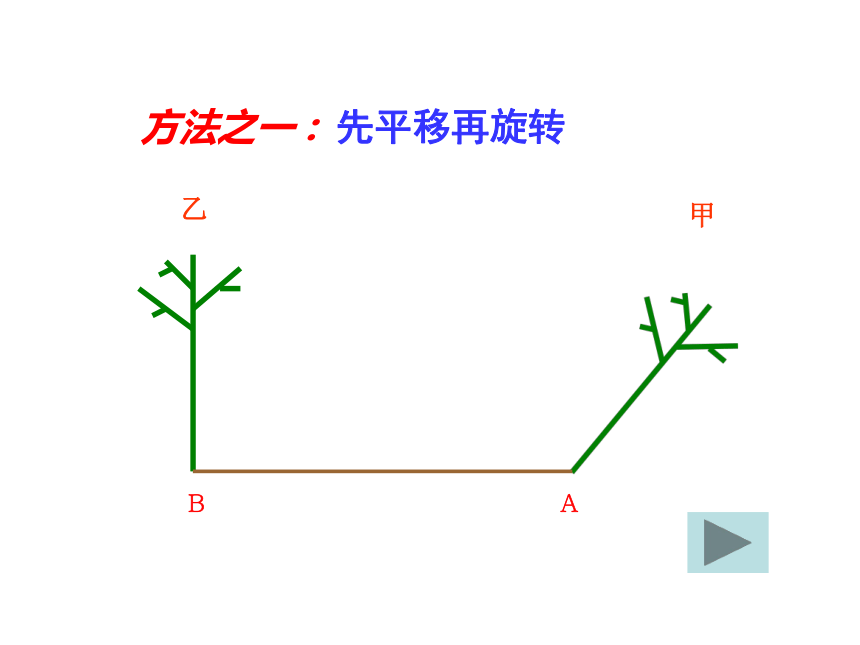
旋转角对称轴对应点的连线段对应点的连线段的垂直平分线的交点,对应点 与旋转中心连线的夹角.对应点连线段的垂直平分线例1:怎样将下图中的甲图变成乙图?方法之一 : 先平移再旋转BA甲乙方法之一: 先旋转再平移.BA甲乙BA甲乙练一练:怎样将下图中的甲图变成乙图?两个大小相等、相同图形的图形的变换方式有哪些?4、复合变换。观察下图它是由八个小“十字”组成,
请你用各种变换分析这个图形方法一 : 由一个 小“十字”连续平移七次.方法二:两个红色的小“十字”绕着图案的中心,逆时针分别旋转90o,180o,270o前后图形组成.OEFGH 2.作这两部分关于GH的轴对称图形.1.两个红色小“十字”作关于EF的轴对称图形.方法三 1.两个红色的小“十字 ”平移形成图形的左侧. 2.左右部分一起绕图形的中心顺时针旋转90o.
方法四方法五1.两个红色的小”十”字绕图形中心逆时针旋转90°.2.作这两部分关于EF的轴对称图形.方法六以四个小“十”字为基本图案,作关于EF的轴对称图形下面的图案是由12个等边三角形所组成,它可以看做是以一个什么图案为“基本图案”,通过一种变换形成的?由两个等边三角形所组成的菱形绕图形的中心旋转五次,旋转角分别为__、__、__、__、__.由四个等边三角形组成的“ ”图形旋转而成下图中有几个三角形是由△ABC怎样平移变换而成的?思考一:如果一个图形与另一个图形大小相等、形状相同,如何判断它们是一种图形变换?还是复合变换?平移变换?各组对应点的连线是否平行且相等?轴对称变换?对应点的连线段是否平行,且被同一条直线垂直平分?旋转变换?对应点的连线段的垂直平分线是否相交于一点?o思考二:两个形状相同、大小相等的两
个图形是否通过两次变换均能重合?思考三:如果我们把 图案换成 原来的几种变换还成立吗?1、综合利用平移、旋转、轴对称探索图形之间的变换关系,分析复合图案的形成过程。2、简单的基本图案经过平移、旋转、轴对称变换或复合变换可以得到美丽的复合图案。3、欣赏图案的同时,体会图案设计者的意图和意境。这节课你有什么收获?谢 谢随堂练习如图,怎样将右边的图形变成左边的图形?随堂练习 下图是由三个正三角形拼成的,它可以看做
由其中一个三角形经过怎样的变化而得到?BCA 方法一:
把△ABC看作基本图
案,以A点为旋转中心,
分别按顺时针、逆时针
方向旋转60o。BCA 方法二 : 把△ABC看作基本图案,分别以AB、AC所在直线为
对称轴作轴对称图形。
把握住这种"变换",
也就把握住未来.南京外国语学校 苏竹青mathmath它们是怎么变过来的?mathmath1、图形的变换我们学习了哪几种形式? 平移、旋转、轴对称不变是图形的形状和大小,
改变的是图形的位置.2、在变换过程中有哪些不变?哪些改变了?下面的图案可以看做是以一个什么图案为“基本图案”形成的?试用多种方法分析它的形成过程。
如图所示的(2)、(3)、(4)是由基本图形(1)通过怎样的变换得到的?请你分析解释这几个图形.(1)(2)(3)(4)a、对应点所连的线段平行且相等.
b、对应线段平行且相等.
c、对应角相等.Oa、图形上的每一点绕中心沿相同的方向旋转
b、旋转角相等;
c、对应点到旋转中心的距离相等.对应点的连线段平行且被对称轴垂直平分1、平移变换:我们如何确定它的2、旋转变换:我们如何确定它的3、轴对称变换:我们如何确定它的方向与距离旋转中心与
旋转角对称轴对应点的连线段对应点的连线段的垂直平分线的交点,对应点 与旋转中心连线的夹角.对应点连线段的垂直平分线例1:怎样将下图中的甲图变成乙图?方法之一 : 先平移再旋转BA甲乙方法之一: 先旋转再平移.BA甲乙BA甲乙练一练:怎样将下图中的甲图变成乙图?两个大小相等、相同图形的图形的变换方式有哪些?4、复合变换。观察下图它是由八个小“十字”组成,
请你用各种变换分析这个图形方法一 : 由一个 小“十字”连续平移七次.方法二:两个红色的小“十字”绕着图案的中心,逆时针分别旋转90o,180o,270o前后图形组成.OEFGH 2.作这两部分关于GH的轴对称图形.1.两个红色小“十字”作关于EF的轴对称图形.方法三 1.两个红色的小“十字 ”平移形成图形的左侧. 2.左右部分一起绕图形的中心顺时针旋转90o.
方法四方法五1.两个红色的小”十”字绕图形中心逆时针旋转90°.2.作这两部分关于EF的轴对称图形.方法六以四个小“十”字为基本图案,作关于EF的轴对称图形下面的图案是由12个等边三角形所组成,它可以看做是以一个什么图案为“基本图案”,通过一种变换形成的?由两个等边三角形所组成的菱形绕图形的中心旋转五次,旋转角分别为__、__、__、__、__.由四个等边三角形组成的“ ”图形旋转而成下图中有几个三角形是由△ABC怎样平移变换而成的?思考一:如果一个图形与另一个图形大小相等、形状相同,如何判断它们是一种图形变换?还是复合变换?平移变换?各组对应点的连线是否平行且相等?轴对称变换?对应点的连线段是否平行,且被同一条直线垂直平分?旋转变换?对应点的连线段的垂直平分线是否相交于一点?o思考二:两个形状相同、大小相等的两
个图形是否通过两次变换均能重合?思考三:如果我们把 图案换成 原来的几种变换还成立吗?1、综合利用平移、旋转、轴对称探索图形之间的变换关系,分析复合图案的形成过程。2、简单的基本图案经过平移、旋转、轴对称变换或复合变换可以得到美丽的复合图案。3、欣赏图案的同时,体会图案设计者的意图和意境。这节课你有什么收获?谢 谢随堂练习如图,怎样将右边的图形变成左边的图形?随堂练习 下图是由三个正三角形拼成的,它可以看做
由其中一个三角形经过怎样的变化而得到?BCA 方法一:
把△ABC看作基本图
案,以A点为旋转中心,
分别按顺时针、逆时针
方向旋转60o。BCA 方法二 : 把△ABC看作基本图案,分别以AB、AC所在直线为
对称轴作轴对称图形。
