锐角三角函数(1)[下学期]
图片预览




文档简介
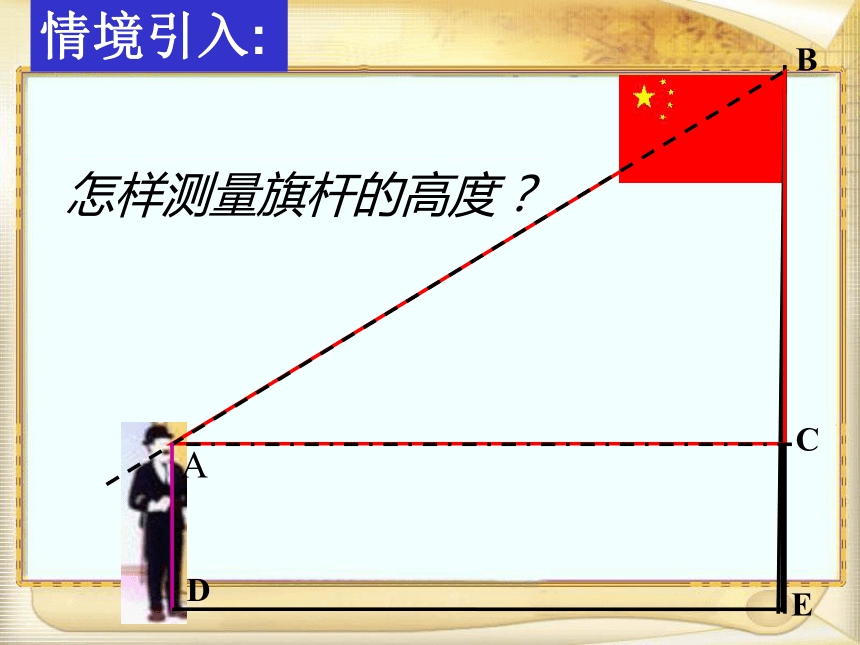
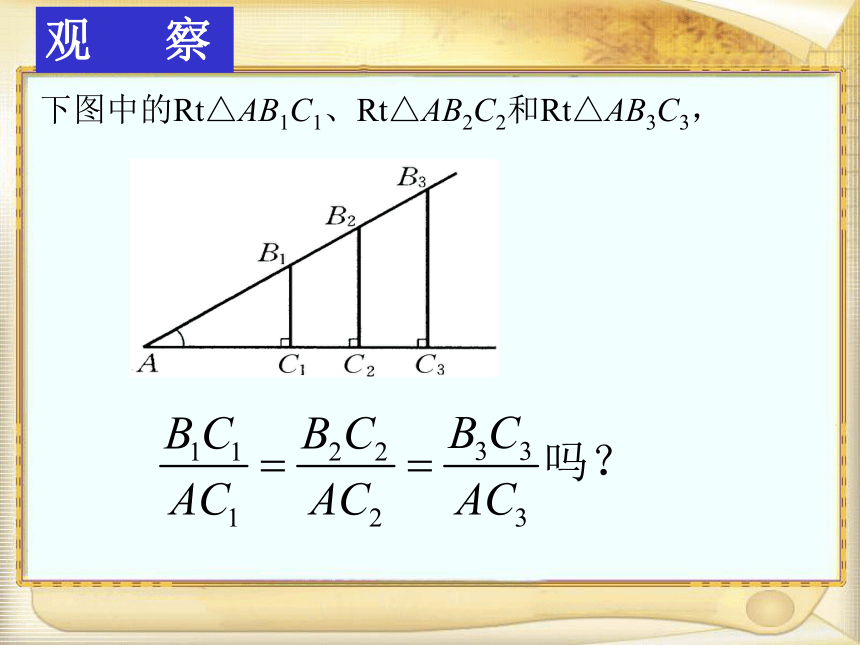
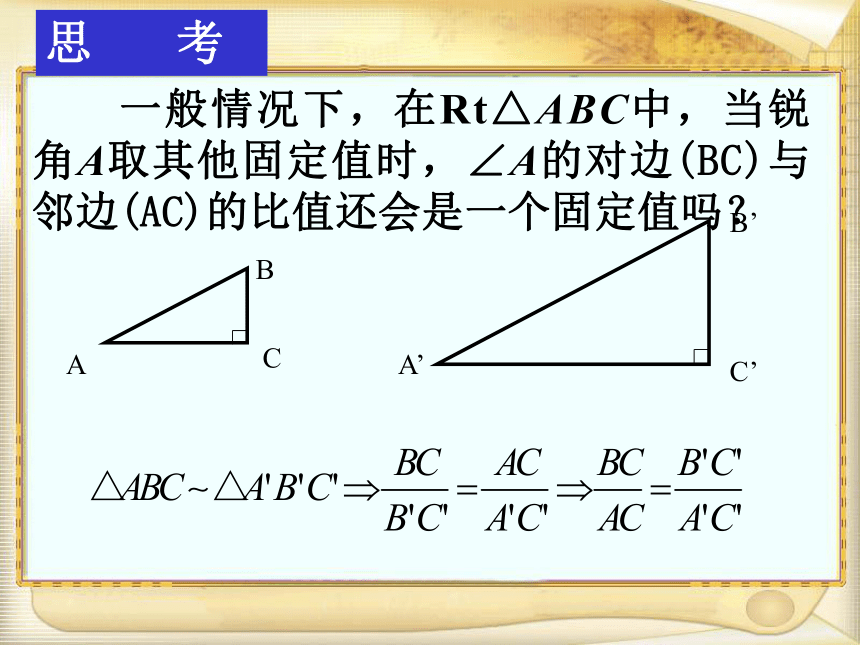
课件27张PPT。锐角三角函数(1)授课:华师附中 聂少林情境引入:怎样测量旗杆的高度?ADBCE下图中的Rt△AB1C1、Rt△AB2C2和Rt△AB3C3,观 察 一般情况下,在Rt△ABC中,当锐角A取其他固定值时,∠A的对边(BC)与邻边(AC)的比值还会是一个固定值吗? 思 考ABCA’B’C’★ 在直角三角形中,只要锐角取一_______ ,该直角三角形任意两边之比便是一个______ 。 定值定值
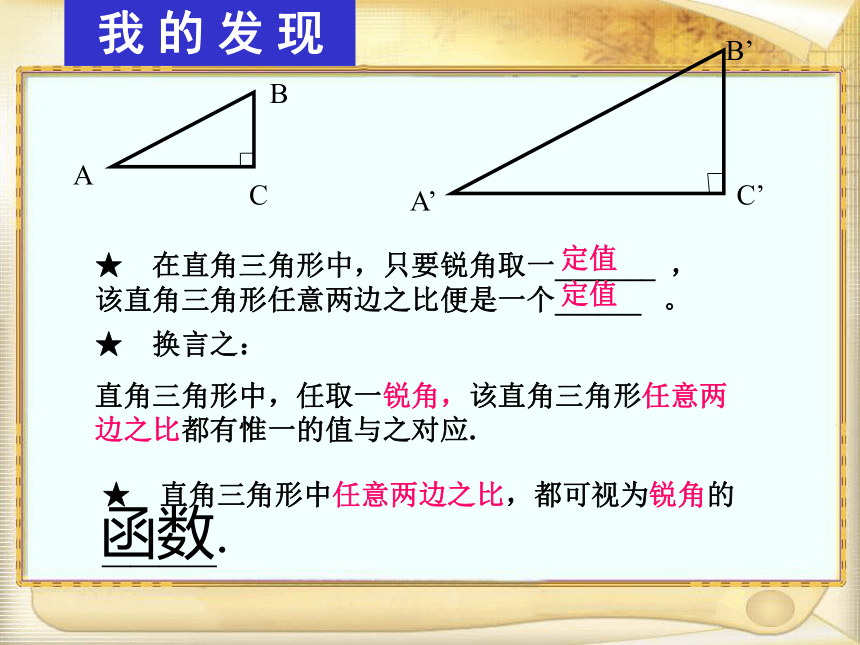
★ 换言之:
直角三角形中,任取一锐角,该直角三角形任意两边之比都有惟一的值与之对应.
★ 直角三角形中任意两边之比,都可视为锐角的
————函数.ABCA’B’C’ 我 的 发 现概 括 在Rt△ABC中,对于A的每一个确定的值,其对边与斜边、邻边与斜边、邻边与对边、对边与邻边等比值唯一确定,这几个比值都是锐角A的三角函数。记作 sin A、cos A、tan A、cot A 如图,在Rt△MNP中,∠N=90゜.
∠P的对边是________,∠P的邻边是______;
∠M的对边是_______,∠M的邻边是______; 你知道吗自学课本P108, 画图说明
什么叫做一个锐角的
正弦
余弦
正切
余切锐角三角函数的定义∠A的正弦,记作:
sin A=
余弦:cos A=
正切:tan A=
余切:cot A=
锐角三角函数的定义
锐角三角函数的定义注意2.sinA,cosA,tanA,cotA都是整体符号,不能看成sin·A, cos · A, tan · A, cot · A1.当角A固定时,它的三角函数值都是固定的,与角A的边长短无关.3.若用三个大写字母表示一个角时,在表示它的三角函数时,角的符号“∠”不能省略.2、tan A?cot A=___.根据函数的比值思考:
1、 sin A,cos A, tanA, cotA的取值范围怎样?发现·交流1. 如图,求出Rt△DEC(∠E=90゜)中∠D的四个三角函数值. 说一说 写一写2、在下列括号内填写适当线段
sinA= =
sinB= =
cos∠ACD= = cos___
cos∠BCD = = cos___ACBCCDABCDBCACDABBCACACCDAB画一画 写一写1.如图,在Rt△ABC中,∠ACB=90°, BC=5,AC=4, (1)求sinA ,sinB的值, (2)过点C作CD⊥AB,求cos∠ACD.规范解题2.在等腰△ABC中,AB=AC=13,BC=10,
求tanB,cotC.求锐角三角函数时,勾股定理的运用是很重要的.规范解题反馈练习1.在△ABC中,∠C=90°,BC=3,tanB=
则AB= 。
2.在△ABC中,∠C=90°,如果tanA= ,那么sinB=( )。
A B C D
3.在△ABC中,已知AC=3,BC=4,AB=5,那么下列结论成立的是( )。
A sinA= B cosA=
C tanA= D cotA=4.如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定5.已知∠A,∠B为锐角
(1)若∠A=∠B,则tanA tanB;
(2)若tanA=tanB,则∠A ∠B.反馈练习 6.sinA=2m-3(A为锐角),则m的取值范围是___.1.在Rt△ABC中,∠C=90°,sinA= , 求∠B的四个三角函数值。解 在Rt△ABC中,由sinA=
可设BC=4k,AB=5k,k≠0则
有AC=
∴sinB= ,cosB=
tanB= ,cotB=实践应用ABC┌ 2.在Rt△ABC中,∠C=900,BC=5,
cosB= 求AC的值.
实践应用课堂探究与提高(一)1、tan A?cot A=___(同角三角函数关系式)在△ABC中,当∠A为锐角时,根据定义分析、计算:在△ABC中,当∠A+∠B=900时,根据定义分析:3.tanA与cotB, cotA与tanB呢?2.cos A与sin B有什么关系?课堂探究与提高(二)1.sin A与cos B有什么关系?(互为余角的三角函数之间的关系)拓展与提高2.已知∠A为锐角,且tanA·tan200=1,则∠A=___.1.已知α为锐角,tanα=3,则cotα-sin2α=___.在Rt△ABC中,∠C=90°,
sinA= ,cosA= ,
tanA= ,cotA= 。 其中0<sin A<1, 0<cos A<1,
tanA>0, cotA>0锐角三角函数的意义小结:同角三角函数关系式互为余角的三角函数之间的关系锐角三角函数描述了直角三角形中边与角的关系,它又是变量之间重要的函数关系,即新奇,又富有魅力,你可要与它建立好感情噢! 结束寄语作业:黄冈点练P89
★ 换言之:
直角三角形中,任取一锐角,该直角三角形任意两边之比都有惟一的值与之对应.
★ 直角三角形中任意两边之比,都可视为锐角的
————函数.ABCA’B’C’ 我 的 发 现概 括 在Rt△ABC中,对于A的每一个确定的值,其对边与斜边、邻边与斜边、邻边与对边、对边与邻边等比值唯一确定,这几个比值都是锐角A的三角函数。记作 sin A、cos A、tan A、cot A 如图,在Rt△MNP中,∠N=90゜.
∠P的对边是________,∠P的邻边是______;
∠M的对边是_______,∠M的邻边是______; 你知道吗自学课本P108, 画图说明
什么叫做一个锐角的
正弦
余弦
正切
余切锐角三角函数的定义∠A的正弦,记作:
sin A=
余弦:cos A=
正切:tan A=
余切:cot A=
锐角三角函数的定义
锐角三角函数的定义注意2.sinA,cosA,tanA,cotA都是整体符号,不能看成sin·A, cos · A, tan · A, cot · A1.当角A固定时,它的三角函数值都是固定的,与角A的边长短无关.3.若用三个大写字母表示一个角时,在表示它的三角函数时,角的符号“∠”不能省略.2、tan A?cot A=___.根据函数的比值思考:
1、 sin A,cos A, tanA, cotA的取值范围怎样?发现·交流1. 如图,求出Rt△DEC(∠E=90゜)中∠D的四个三角函数值. 说一说 写一写2、在下列括号内填写适当线段
sinA= =
sinB= =
cos∠ACD= = cos___
cos∠BCD = = cos___ACBCCDABCDBCACDABBCACACCDAB画一画 写一写1.如图,在Rt△ABC中,∠ACB=90°, BC=5,AC=4, (1)求sinA ,sinB的值, (2)过点C作CD⊥AB,求cos∠ACD.规范解题2.在等腰△ABC中,AB=AC=13,BC=10,
求tanB,cotC.求锐角三角函数时,勾股定理的运用是很重要的.规范解题反馈练习1.在△ABC中,∠C=90°,BC=3,tanB=
则AB= 。
2.在△ABC中,∠C=90°,如果tanA= ,那么sinB=( )。
A B C D
3.在△ABC中,已知AC=3,BC=4,AB=5,那么下列结论成立的是( )。
A sinA= B cosA=
C tanA= D cotA=4.如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定5.已知∠A,∠B为锐角
(1)若∠A=∠B,则tanA tanB;
(2)若tanA=tanB,则∠A ∠B.反馈练习 6.sinA=2m-3(A为锐角),则m的取值范围是___.1.在Rt△ABC中,∠C=90°,sinA= , 求∠B的四个三角函数值。解 在Rt△ABC中,由sinA=
可设BC=4k,AB=5k,k≠0则
有AC=
∴sinB= ,cosB=
tanB= ,cotB=实践应用ABC┌ 2.在Rt△ABC中,∠C=900,BC=5,
cosB= 求AC的值.
实践应用课堂探究与提高(一)1、tan A?cot A=___(同角三角函数关系式)在△ABC中,当∠A为锐角时,根据定义分析、计算:在△ABC中,当∠A+∠B=900时,根据定义分析:3.tanA与cotB, cotA与tanB呢?2.cos A与sin B有什么关系?课堂探究与提高(二)1.sin A与cos B有什么关系?(互为余角的三角函数之间的关系)拓展与提高2.已知∠A为锐角,且tanA·tan200=1,则∠A=___.1.已知α为锐角,tanα=3,则cotα-sin2α=___.在Rt△ABC中,∠C=90°,
sinA= ,cosA= ,
tanA= ,cotA= 。 其中0<sin A<1, 0<cos A<1,
tanA>0, cotA>0锐角三角函数的意义小结:同角三角函数关系式互为余角的三角函数之间的关系锐角三角函数描述了直角三角形中边与角的关系,它又是变量之间重要的函数关系,即新奇,又富有魅力,你可要与它建立好感情噢! 结束寄语作业:黄冈点练P89
