【全国百强校】江西省师大附中高中数学必修1第二章第二节第三课时《映射的概念》教学课件(北师大版,36张PPT)
文档属性
| 名称 | 【全国百强校】江西省师大附中高中数学必修1第二章第二节第三课时《映射的概念》教学课件(北师大版,36张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-06-27 15:45:35 | ||
图片预览










文档简介
课件36张PPT。 映射的概念
江西师大附中一层练习:
1、在初中我们已学过一些对应的例子:(请同学
们思考、讨论)
①看电影时,电影票与座位之间存在着 的 关系.
⑤实数和数轴上的点存在着 的关系②坐标平面内的点和有序实数对(x, y)之间存在着
的关系.
③三角形和它的面积之间存在 的关系.④高一4班的每一个学生与学号之间存
在 的关系.
对应一一对应对应对应一一对应下面我们将学习一种特殊的对应------
?
映 射二层练习:
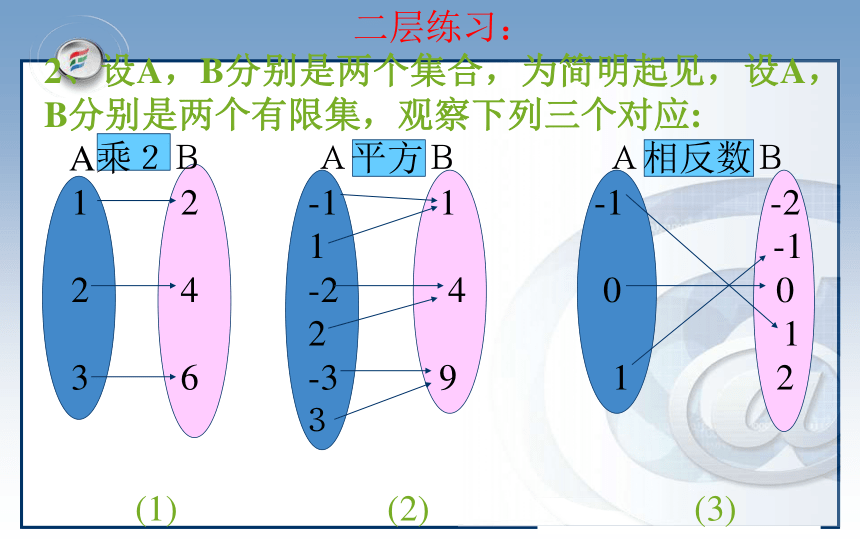
2、设A,B分别是两个集合,为简明起见,设A,B分别是两个有限集,观察下列三个对应:
? A乘2B A平方B A相反数B
1 2 -1 1 -1 -2
1 -1
2 4 -2 4 0 0
2 1
3 6 -3 9 1 2
3
(1) (2) (3)
这些对应的共同特点是什么?
答:对于左边集合A中的任何
一个元素,在右边集合B中都
有唯一的元素和它对应。 返回小 结:映射:设A,B是两个集合,如果按照某种对应法则f,对于集合A中的任何一个元素,在集合B中都有唯一的元素和它对应,这样的对应(包括集合A、B以及A到B的对应法则f)叫做集合A到集合B的映射。 记作:f:A B返回像、原像:给定一个集合A到集合B
的映射,且a属于A,b属于B,如果
元素a和元素b对应,则元素b叫做
元素a的像,元素a叫做元素b的原像.
①“A到B”:映射是有方向的,A到B的映射与B到 A的映射往往不是同一个映射,A到B是求平方,B到A则是开平方,因此映射是有序的;
②“任一”:就是说对集合A中任何一个元素,集合B中都有元素和它对应,这是映射的存在性;
③“唯一”:对于集合A中的任何一个元素,集合B中都是唯一的元素和它对应,这是映射的唯一性;
④“在集合B中”:也就是说A中元素的象必在集合B中,这是映射的封闭性。
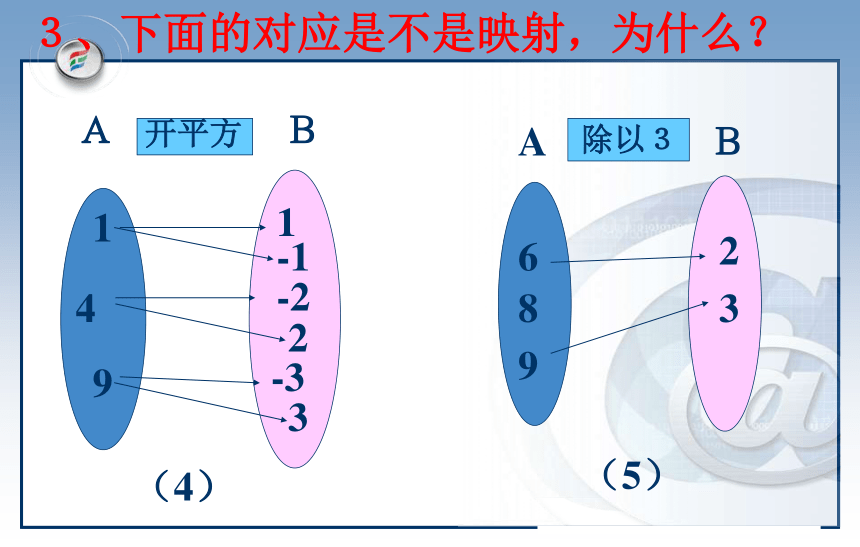
说 明: 3、下面的对应是不是映射,为什么?
932 -3-21(4)41-1(5)68923除以3 BA开平方 AB解:(4) 因为集合A中的每一个元素,在集合B中都有两个元素与之相对应,不满足唯一性,因此,它不是集合A到集合B的映射。(5) 集合A中元素8,在集合B中没有元素和它对应,不满足存在性,因此,它不是集合A到集合B的映射。
4、思考:如果以对应来说,什么样的对应才是一个映射?
一对一,多对一是映射.
但一对多显然不是映射.
①任意性:映射中的两个集合A,B可以是数集、点集或由图形组成的集合等;
②有序性:映射是有方向的,A到B的映射与B到A的映射往往不是同一个映射;
③存在性:映射中集合A的每一个元素在集合B中都有它的象;
返回小 结:
④唯一性:映射中集合A的任一元素在集合B中的象是唯一的;
⑤封闭性:映射中集合A的任一元素的象都必须是B中的元素,不要求B中的每一个元素都有原象,即A中元素的象集是B的子集。
小 结:映射三要素:
①集合A;
②集合 B;
③对应法则.
三者缺一不可; 所以记为f:A B返回函数与映射的区别和 联系函数是一种特殊的映射,是从非空数集到非空数集的映射。
函数也可叙述为:设A,B是两个非空数集,f是A到B 的一个映射,那么映射f:A→B称为A到B的函数函数中原像集合称为定义域,像的集合称为值域特殊的映射——一 一映射
1.A中每一个元素在B中都有唯一的像与之对应; 2.A中的不同元素的像也不同;3.B中的每一个元素都有原像。有时,我们把集合A,B之间的一 一映射也叫作一一 对应它满足下列条件
4、判断下列对应是否映射,一 一映射?有没有对应法则?
a d a e a e
b e b f b f
c f c g c g
d d
(A) (B) (C)三层练习:4、解:
(A)是映射,对应法则是a → d,b → e,c → f;是一一映射;
(B)是映射,对应法则是a → d,b → e,c → f;不是一一映射;
(C)不是映射,因为元素d没有像,不是一 一映射。
5、下列各组映射是否同一映射?
a e a e a e
b f b f b f
c g c g c g
(A) (B) (C)
5、解: 不是同一映射
因为它们的对应法则
各不相同;
6、判断下列两个对应是否是集合A到集合B的映射?是否是一一映射?
A f:x 2x+1B Af:x x除以2B
的余数
1 3 1
4 2 0
2 5 3
6 4 1
3 7 …
8
4 9
(A) (B)
A f:x x的 B Af:x x除以3 B
倒数 的余数
1 1 0
2 1/2 1 0
3 1/3 2 1
4 1/4 3 2
5 … …
(C) (D)
6、解:(A),(B),(D)都是映射;
而(C)不是映射,因为集A中的元素
5没有象.它们都不是映射。
四层练习:
7、设A={1,2,3,4},B={3,4,5,6,7,8,9},集合A中的元素x按照对应法则“乘2加1”和集合B中的元素2x+1对应.这个对应是不是映射?
是,因为1→ 3,2 → 5,3→ 7,4→ 9 8 .下面两个集合间的对应关系哪些是从A到B的
一一映射?哪些是函数?(1)A={你们班的同学},B={体重},f:每个
同学对应自己的体重;
(2)M={1,2,3,4},N={2,4,6,8},
f:n=2m,n ∈N,m ∈M;
(3)X=R,Y={非负实数},f:y= ,x ∈X,y ∈Y。
(1)不是一一映射,也不是函数;(2)是一一映射,
也是函数;(3)不是一一映射,是函数。
本节课学习了以下内容:对应映射的概念,特征,三要素;函数与映射的区别联系一一映射的概念,与映射的区别课堂小结:谢谢
8、设A=N*,B={0,1},集合A中的元素x按照对应法则“x除以2得的余数”和集合B中的元素对应.这个对应是不是映射?
是,因为1=0×2+1,2=1×2+0,
3=1×2+1,4=2×2+0,
…
9、下面说法正确的是( )
(A)对于任意两个集合A与B,都可以建立一个从 集合A到集合B的映射
(B)对于两个无限集合A与B,一定不能建立一个 从集合A到集合B的映射
(C)如果集合A中只有一个元素,B为任一非空集
合,那么从集合A到集合B只能建立一个映射
(D)如果集合B只有一个元素,A为任一非空集合, 则从集合A到集合B只能建立一个映射
D
10、A=Z,B=N*,集合A中的元素x按照对应法则“求绝对值”和集合B中的元素对应.这个对应是不是映射?
不是,集A中的元素0没有象
11、A={0,1,2,4},B={0,1,4,9,64},集合A中的元素x按照对应法则:
f :a b=(a?1) 和集合B中的元素对应.这个对应是不是映射?是2
12、在从集合A到集合B的映射中,说法 正确的是( )
(A)B中的某一个元素b的原象可能不唯一(B)A中的某一个元素a的象可能不唯一
(C)A中的两个不同元素所对应的象必不 相同
(D)B中的两个不同元素的原象可能相同A
课堂小结:
本节课学习了以下内容:
对应:
映射概念,一一映射:
特征:
要素:
作业:
P.52
习题2.1:4,5谢 谢 配 合
再见
江西师大附中一层练习:
1、在初中我们已学过一些对应的例子:(请同学
们思考、讨论)
①看电影时,电影票与座位之间存在着 的 关系.
⑤实数和数轴上的点存在着 的关系②坐标平面内的点和有序实数对(x, y)之间存在着
的关系.
③三角形和它的面积之间存在 的关系.④高一4班的每一个学生与学号之间存
在 的关系.
对应一一对应对应对应一一对应下面我们将学习一种特殊的对应------
?
映 射二层练习:
2、设A,B分别是两个集合,为简明起见,设A,B分别是两个有限集,观察下列三个对应:
? A乘2B A平方B A相反数B
1 2 -1 1 -1 -2
1 -1
2 4 -2 4 0 0
2 1
3 6 -3 9 1 2
3
(1) (2) (3)
这些对应的共同特点是什么?
答:对于左边集合A中的任何
一个元素,在右边集合B中都
有唯一的元素和它对应。 返回小 结:映射:设A,B是两个集合,如果按照某种对应法则f,对于集合A中的任何一个元素,在集合B中都有唯一的元素和它对应,这样的对应(包括集合A、B以及A到B的对应法则f)叫做集合A到集合B的映射。 记作:f:A B返回像、原像:给定一个集合A到集合B
的映射,且a属于A,b属于B,如果
元素a和元素b对应,则元素b叫做
元素a的像,元素a叫做元素b的原像.
①“A到B”:映射是有方向的,A到B的映射与B到 A的映射往往不是同一个映射,A到B是求平方,B到A则是开平方,因此映射是有序的;
②“任一”:就是说对集合A中任何一个元素,集合B中都有元素和它对应,这是映射的存在性;
③“唯一”:对于集合A中的任何一个元素,集合B中都是唯一的元素和它对应,这是映射的唯一性;
④“在集合B中”:也就是说A中元素的象必在集合B中,这是映射的封闭性。
说 明: 3、下面的对应是不是映射,为什么?
932 -3-21(4)41-1(5)68923除以3 BA开平方 AB解:(4) 因为集合A中的每一个元素,在集合B中都有两个元素与之相对应,不满足唯一性,因此,它不是集合A到集合B的映射。(5) 集合A中元素8,在集合B中没有元素和它对应,不满足存在性,因此,它不是集合A到集合B的映射。
4、思考:如果以对应来说,什么样的对应才是一个映射?
一对一,多对一是映射.
但一对多显然不是映射.
①任意性:映射中的两个集合A,B可以是数集、点集或由图形组成的集合等;
②有序性:映射是有方向的,A到B的映射与B到A的映射往往不是同一个映射;
③存在性:映射中集合A的每一个元素在集合B中都有它的象;
返回小 结:
④唯一性:映射中集合A的任一元素在集合B中的象是唯一的;
⑤封闭性:映射中集合A的任一元素的象都必须是B中的元素,不要求B中的每一个元素都有原象,即A中元素的象集是B的子集。
小 结:映射三要素:
①集合A;
②集合 B;
③对应法则.
三者缺一不可; 所以记为f:A B返回函数与映射的区别和 联系函数是一种特殊的映射,是从非空数集到非空数集的映射。
函数也可叙述为:设A,B是两个非空数集,f是A到B 的一个映射,那么映射f:A→B称为A到B的函数函数中原像集合称为定义域,像的集合称为值域特殊的映射——一 一映射
1.A中每一个元素在B中都有唯一的像与之对应; 2.A中的不同元素的像也不同;3.B中的每一个元素都有原像。有时,我们把集合A,B之间的一 一映射也叫作一一 对应它满足下列条件
4、判断下列对应是否映射,一 一映射?有没有对应法则?
a d a e a e
b e b f b f
c f c g c g
d d
(A) (B) (C)三层练习:4、解:
(A)是映射,对应法则是a → d,b → e,c → f;是一一映射;
(B)是映射,对应法则是a → d,b → e,c → f;不是一一映射;
(C)不是映射,因为元素d没有像,不是一 一映射。
5、下列各组映射是否同一映射?
a e a e a e
b f b f b f
c g c g c g
(A) (B) (C)
5、解: 不是同一映射
因为它们的对应法则
各不相同;
6、判断下列两个对应是否是集合A到集合B的映射?是否是一一映射?
A f:x 2x+1B Af:x x除以2B
的余数
1 3 1
4 2 0
2 5 3
6 4 1
3 7 …
8
4 9
(A) (B)
A f:x x的 B Af:x x除以3 B
倒数 的余数
1 1 0
2 1/2 1 0
3 1/3 2 1
4 1/4 3 2
5 … …
(C) (D)
6、解:(A),(B),(D)都是映射;
而(C)不是映射,因为集A中的元素
5没有象.它们都不是映射。
四层练习:
7、设A={1,2,3,4},B={3,4,5,6,7,8,9},集合A中的元素x按照对应法则“乘2加1”和集合B中的元素2x+1对应.这个对应是不是映射?
是,因为1→ 3,2 → 5,3→ 7,4→ 9 8 .下面两个集合间的对应关系哪些是从A到B的
一一映射?哪些是函数?(1)A={你们班的同学},B={体重},f:每个
同学对应自己的体重;
(2)M={1,2,3,4},N={2,4,6,8},
f:n=2m,n ∈N,m ∈M;
(3)X=R,Y={非负实数},f:y= ,x ∈X,y ∈Y。
(1)不是一一映射,也不是函数;(2)是一一映射,
也是函数;(3)不是一一映射,是函数。
本节课学习了以下内容:对应映射的概念,特征,三要素;函数与映射的区别联系一一映射的概念,与映射的区别课堂小结:谢谢
8、设A=N*,B={0,1},集合A中的元素x按照对应法则“x除以2得的余数”和集合B中的元素对应.这个对应是不是映射?
是,因为1=0×2+1,2=1×2+0,
3=1×2+1,4=2×2+0,
…
9、下面说法正确的是( )
(A)对于任意两个集合A与B,都可以建立一个从 集合A到集合B的映射
(B)对于两个无限集合A与B,一定不能建立一个 从集合A到集合B的映射
(C)如果集合A中只有一个元素,B为任一非空集
合,那么从集合A到集合B只能建立一个映射
(D)如果集合B只有一个元素,A为任一非空集合, 则从集合A到集合B只能建立一个映射
D
10、A=Z,B=N*,集合A中的元素x按照对应法则“求绝对值”和集合B中的元素对应.这个对应是不是映射?
不是,集A中的元素0没有象
11、A={0,1,2,4},B={0,1,4,9,64},集合A中的元素x按照对应法则:
f :a b=(a?1) 和集合B中的元素对应.这个对应是不是映射?是2
12、在从集合A到集合B的映射中,说法 正确的是( )
(A)B中的某一个元素b的原象可能不唯一(B)A中的某一个元素a的象可能不唯一
(C)A中的两个不同元素所对应的象必不 相同
(D)B中的两个不同元素的原象可能相同A
课堂小结:
本节课学习了以下内容:
对应:
映射概念,一一映射:
特征:
要素:
作业:
P.52
习题2.1:4,5谢 谢 配 合
再见
