【全国百强校】江西省师大附中高中数学必修1第二章第二节第一课时《函数的概念》教学课件(北师大版,13张PPT)
文档属性
| 名称 | 【全国百强校】江西省师大附中高中数学必修1第二章第二节第一课时《函数的概念》教学课件(北师大版,13张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 789.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-06-27 00:00:00 | ||
图片预览



文档简介
课件13张PPT。函数的概念 1.请回忆在初中我们学过那些函数?并说出其图象和性质正比例函数:y=kx (k≠0)
反比例函数:y=k/x (k≠0)
一次函数y=kx+b (k≠0)
二次函数y=ax2+bx+c (a≠0)
2.什么是函数呢?初中定义:一般地,设在一个变化过程中有两个变量x、y,如果对于x的每一个值,y都有唯一的值与它对应,那么就说x是自变量,y是x的函数。问:y=1(x∈R)是函数吗?
函数的定义一般地,我们有:
设A、B是非空数集,如果按照某种确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么称f:A→B为从集合A到集合B的一个函数(fun_ction),记作:y=f(x), x ∈ A(1)f——对应法则
(2)A ——定义域
(3)C={f(x)|x∈A}——值域y
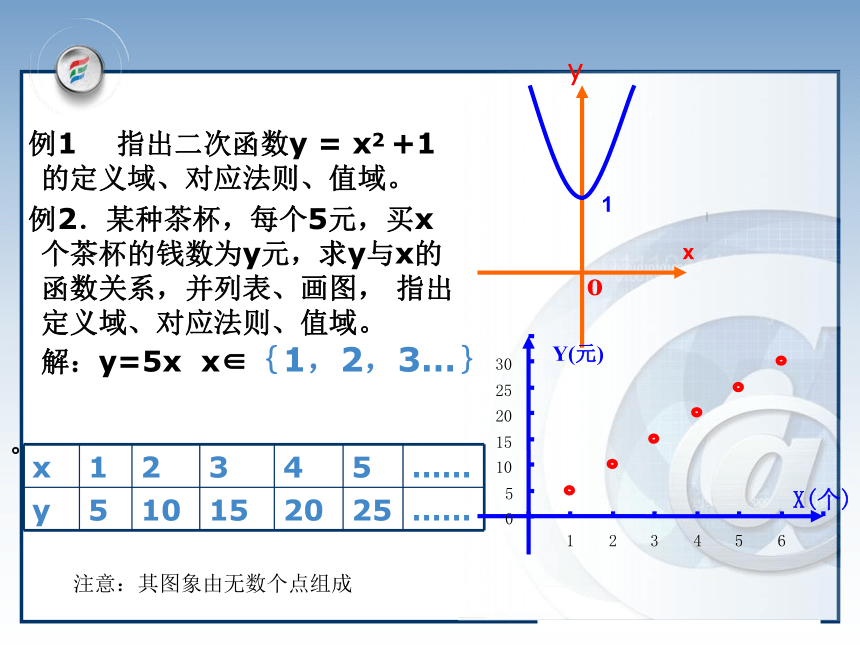
例1 指出二次函数y = x2 +1的定义域、对应法则、值域。
例2.某种茶杯,每个5元,买x 个茶杯的钱数为y元,求y与x的 函数关系,并列表、画图, 指出定义域、对应法则、值域。 解:y=5x x∈{1,2,3…}
。1x注意:其图象由无数个点组成
1函数的定义域、对应法则、值域称为函数的三要素
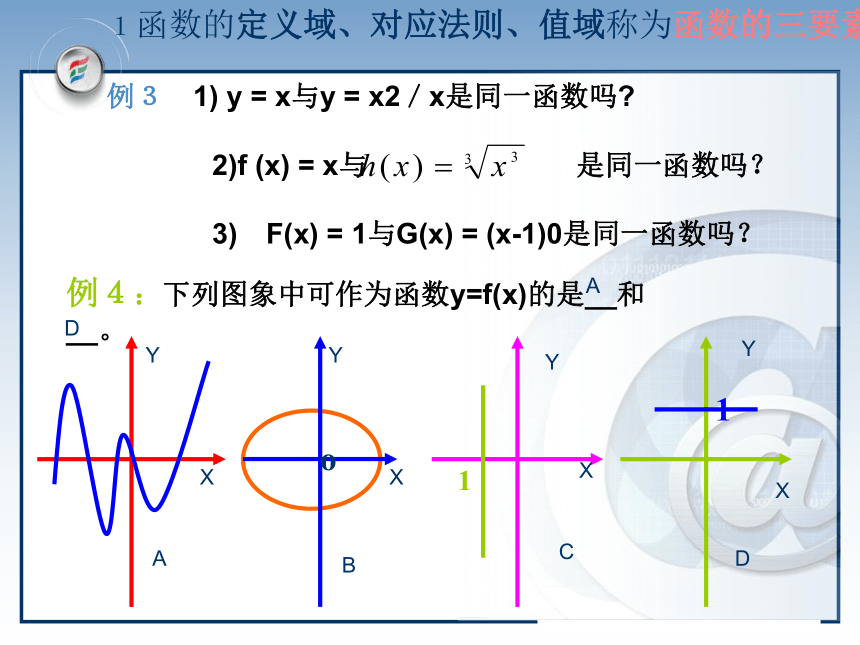
例3 1) y = x与y = x2/x是同一函数吗?
2)f (x) = x与 是同一函数吗?
3) F(x) = 1与G(x) = (x-1)0是同一函数吗?
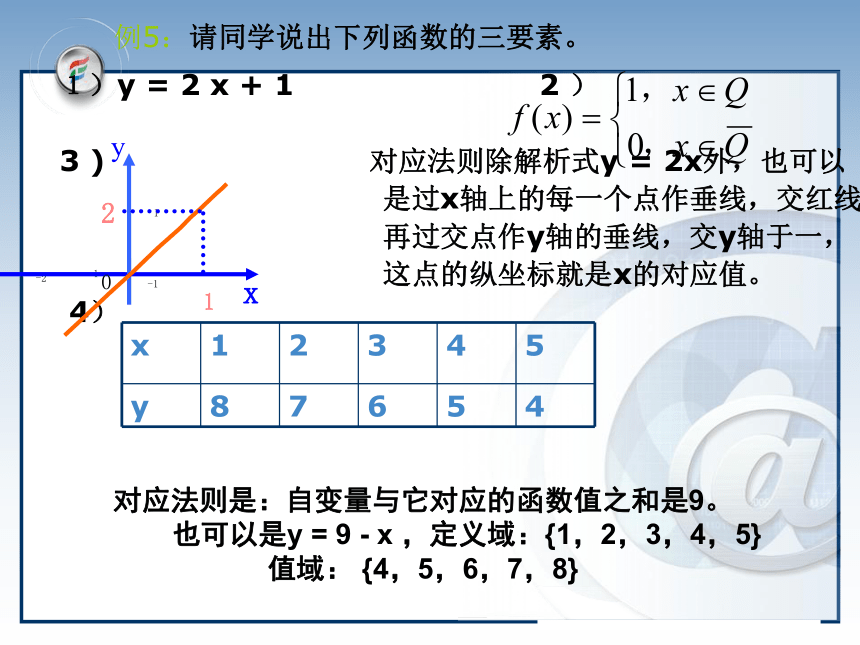
例4:下列图象中可作为函数y=f(x)的是__和__。ABCDYXYXYXYXAD例5:请同学说出下列函数的三要素。1)y = 2 x + 1 2 )
3 ) 对应法则除解析式y = 2x外,也可以
是过x轴上的每一个点作垂线,交红线
再过交点作y轴的垂线,交y轴于一,
这点的纵坐标就是x的对应值。
4)
-11-2-1对应法则是:自变量与它对应的函数值之和是9。
也可以是y = 9 - x ,定义域:{1,2,3,4,5} 值域: {4,5,6,7,8} 8.介绍区间符号:a≤x≤b,记作 [a,b],读作闭区间a、b;
aa≤xa一般地,设实数a < b 则我们把实数集R记作(-∞,+∞), ∞ 读作无穷大;-∞ 读作负无穷大;+∞ 读作正无穷大;“∞”不是一个数,表示无限大的变化趋势,因此作为端点,不用方括号。
x≥a, 记作[a, +∞ ); x>a, 记(a,+∞ ) ;
x≤b, 记作(-∞ ,b]; x学生练习:用区间表示下列实数集合。
{|-18≤x<6 };
{x|x>6}∩{x|-5 {x|-2≤x<6}∪{x|3
2)
3)
4) y = 2x – 1 (3 < y < 5) 注意这个函数有人为限制,已知值域反过来求定义域。
5) s= , 为圆半径。 注意要使实际问题有意义。其图象不是圆。
例7:求f(x) 若 ,求f (0),f (1),f (x2),
若f (x+1) = x2 +2x –3 ,求 f (x),
3)若f (x) = x 2 – x + 3,求 f(X+1 ), 。
4) 若f (x) = x + ,求f [f (x)] (迭代方程)
5)若 , 求f (x)。 注意:
1.当f (x) 是一个解析式时,如果把x,y看作是并列的未知量 或者点的坐标,那么y= f (x)也可以看作是一个方程,例如二次函数y=x2,也可看作是一条抛物线的方程,即二元二次方程一次函数y = x +1也可看作是一元一次方程。
2.y = f (x)表示y是x的函数,但f (x)不一定是解析式。
课堂练习小结这节课我们学习了以下内容函数的概念
函数三要素
区间表示法本节课到此结束,谢谢大家
反比例函数:y=k/x (k≠0)
一次函数y=kx+b (k≠0)
二次函数y=ax2+bx+c (a≠0)
2.什么是函数呢?初中定义:一般地,设在一个变化过程中有两个变量x、y,如果对于x的每一个值,y都有唯一的值与它对应,那么就说x是自变量,y是x的函数。问:y=1(x∈R)是函数吗?
函数的定义一般地,我们有:
设A、B是非空数集,如果按照某种确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么称f:A→B为从集合A到集合B的一个函数(fun_ction),记作:y=f(x), x ∈ A(1)f——对应法则
(2)A ——定义域
(3)C={f(x)|x∈A}——值域y
例1 指出二次函数y = x2 +1的定义域、对应法则、值域。
例2.某种茶杯,每个5元,买x 个茶杯的钱数为y元,求y与x的 函数关系,并列表、画图, 指出定义域、对应法则、值域。 解:y=5x x∈{1,2,3…}
。1x注意:其图象由无数个点组成
1函数的定义域、对应法则、值域称为函数的三要素
例3 1) y = x与y = x2/x是同一函数吗?
2)f (x) = x与 是同一函数吗?
3) F(x) = 1与G(x) = (x-1)0是同一函数吗?
例4:下列图象中可作为函数y=f(x)的是__和__。ABCDYXYXYXYXAD例5:请同学说出下列函数的三要素。1)y = 2 x + 1 2 )
3 ) 对应法则除解析式y = 2x外,也可以
是过x轴上的每一个点作垂线,交红线
再过交点作y轴的垂线,交y轴于一,
这点的纵坐标就是x的对应值。
4)
-11-2-1对应法则是:自变量与它对应的函数值之和是9。
也可以是y = 9 - x ,定义域:{1,2,3,4,5} 值域: {4,5,6,7,8} 8.介绍区间符号:a≤x≤b,记作 [a,b],读作闭区间a、b;
a
x≥a, 记作[a, +∞ ); x>a, 记(a,+∞ ) ;
x≤b, 记作(-∞ ,b]; x
{|-18≤x<6 };
{x|x>6}∩{x|-5
2)
3)
4) y = 2x – 1 (3 < y < 5) 注意这个函数有人为限制,已知值域反过来求定义域。
5) s= , 为圆半径。 注意要使实际问题有意义。其图象不是圆。
例7:求f(x) 若 ,求f (0),f (1),f (x2),
若f (x+1) = x2 +2x –3 ,求 f (x),
3)若f (x) = x 2 – x + 3,求 f(X+1 ), 。
4) 若f (x) = x + ,求f [f (x)] (迭代方程)
5)若 , 求f (x)。 注意:
1.当f (x) 是一个解析式时,如果把x,y看作是并列的未知量 或者点的坐标,那么y= f (x)也可以看作是一个方程,例如二次函数y=x2,也可看作是一条抛物线的方程,即二元二次方程一次函数y = x +1也可看作是一元一次方程。
2.y = f (x)表示y是x的函数,但f (x)不一定是解析式。
课堂练习小结这节课我们学习了以下内容函数的概念
函数三要素
区间表示法本节课到此结束,谢谢大家
