【全国百强校】江西省师大附中高中数学必修5第一章《等差数列等比数列综合练习》教学课件(北师大版,18张PPT)
文档属性
| 名称 | 【全国百强校】江西省师大附中高中数学必修5第一章《等差数列等比数列综合练习》教学课件(北师大版,18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 364.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-06-27 15:46:30 | ||
图片预览






文档简介
课件18张PPT。等差数列等比数列 综合练习教学目的
1、知识目标:系统掌握等差、等比数列定义与性质,灵活应用等差、等比数列的定义与性质解题。
2、能力目标:能综合运用等差数列、等比数列的概念.通项公式、 前 n项和公式和性质解决一些问题.通过对问题的讨论,提高综合分析、解决问题的能力。
3、情感目标:增强学生的运用意识
4、教学重点:等差数列和等比数列的综合运用。
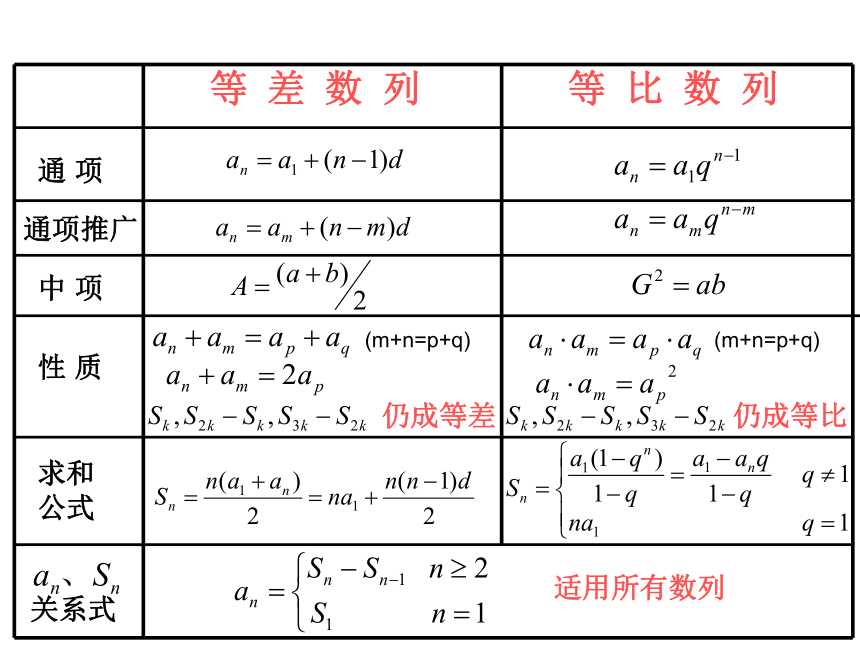
5、教学难点:等差数列和等比数列的综合运用等差数列与等比数列的有关知识比较一览表复习巩固:仍成等差仍成等比等 差 数 列等 比 数 列通 项通项推广中 项性 质求和公式关系式适用所有数列(m+n=p+q)(m+n=p+q) 例1(1). 已知三个数成等差数列,其和为15,其平方和为83,求此三个数.分析:设这三个数为则∴所求三个数分别为3,5,7解得x=5,d=或7,5,3.±2.例1(2):互不相等且依次成等比数列的三个数之积为 ,这三个数适当排列后可排成等差数列,求这三数排成的等差数列.解:设这三个数为 ,则 即:即:与已知三数不等矛盾即:三个数为或即:三个数为或综上:这三数排成的等差数列为:1).若已知三个数成等差数列可将三数设为 或者 ,2.)若已知 三个数成等比数列,则这三个数可设为 ,也可以设为根据具体问题的不同特点而选择不同设法。 为了便于解方程,应该充分分析条件的特征,尽量减少未知数的个数, 用最少的未知数表达出数列的有关项的数量关系,促使复杂的问题转化为较简单的问题,获得最佳的解决方法。一般地:
方法小结例2(1)已知等差数列 满足 ,则 ( )分析:C (2)已知等差数列 前 项和为30,前 项和100,则前 项和为 ( )C(4)、已知等比数列{an}中,an>0且 a2a4+2a3a5+a4a6=25,则a3+a5= ( )
(A)5 (B) 10 (C)15 (D) 20
Aa2a4=(a3)2
a4a6=(a5)2原式=(a3+a5)2=25=> a3+a5=5(an>0)提示:解法小结 掌握好等差数列、等比数列的一些常见性质并在解题中灵活运用,可以简化解题过程,起到事半功倍的效果。例3:已知数列{an}为等差数列,公差d≠0,{an}的部分项组成下列数列: 恰好为等比数列,其中k1=1,k2=5,k3=17,求k1+k2+.....+kn即得出新数列的公比:
再由∴可解出kn,进而求出根据数列{an}是等差数列,通项可写作: an=a1+(n-1)d,可表示出:a1,,a5=a1+4d,a17=a1+16d,再根据a1,a5,a17成等比数列,又可得:(a5)2=a1a17,于是可解出d=(1/2)a1.分析:1、本题是一个等差、等比数列的综合型问题,在解题过程中,分清那一步是用等差数列条件,那一步是用等比数列条件是正确解题的前提。
2。仔细观察,找到两个数列序号间的联系,是使问题得解的关键方法小结 设等差数列 {an} 的公差为d,等比数列 {bn} 的公比为 ,则由题意得解析:通项特征:由等差数列通项与等比数列通项相乘而得求和方法:错位相减法——错项法 解析: 两式相减: 错位相减法1.观察数列:30,37,32,35,34,33,36,( ),38的特点,在括号内适当的一个数是______2.在等比数列中,a4+a6=3,则a5(a3+2a5+a7)=_____3. 在等差数列{an}中,若a4+a6+a8+a10+a12=120,则
2a10-a12的值为 ( )
A.20 B.22 C.24 D.28319C4.已知数列{an}中,a1=1,并且3an+1-3an=1,则a301= ( )
A.100 B.101 C.102 D.103B5.若{an}是等比数列,且an>0,a2a4+2a3a5+a4a6=25,那
么a3+a5的值等于 ( )A.5 B.1 C.15 D.10A课堂练习:6.等差数列{an}中,已知前4项和是1,前8项和是4,则
a17+a18+a19+a20的值等于 ( )A.7 B.8 C.9 D.10C 8.在数列{an}中,a1=3,an+1=an+3n(n≥1),求此数列的通项公式.9.数列{bn}中,b1+b2+b3= ,b1b2b3= ,若{an}是等差数
列,且bn= ,求{an}的通项公式.7、四个数,前三个成等比数列,它们的和是19;后三个成等差数列,和是12,求此四个数.(四数为: 9,6,4,2或25,-10,4,18.)小 结对等差、等比综合问题
1。要正确分清题目究竟是等差还是等比,不能混淆。
2。掌握设元的技巧;
3。要掌握分析数列问题的基本思想方法,把握好等差等比数列各自的特点并在解题中灵活运用。
1、知识目标:系统掌握等差、等比数列定义与性质,灵活应用等差、等比数列的定义与性质解题。
2、能力目标:能综合运用等差数列、等比数列的概念.通项公式、 前 n项和公式和性质解决一些问题.通过对问题的讨论,提高综合分析、解决问题的能力。
3、情感目标:增强学生的运用意识
4、教学重点:等差数列和等比数列的综合运用。
5、教学难点:等差数列和等比数列的综合运用等差数列与等比数列的有关知识比较一览表复习巩固:仍成等差仍成等比等 差 数 列等 比 数 列通 项通项推广中 项性 质求和公式关系式适用所有数列(m+n=p+q)(m+n=p+q) 例1(1). 已知三个数成等差数列,其和为15,其平方和为83,求此三个数.分析:设这三个数为则∴所求三个数分别为3,5,7解得x=5,d=或7,5,3.±2.例1(2):互不相等且依次成等比数列的三个数之积为 ,这三个数适当排列后可排成等差数列,求这三数排成的等差数列.解:设这三个数为 ,则 即:即:与已知三数不等矛盾即:三个数为或即:三个数为或综上:这三数排成的等差数列为:1).若已知三个数成等差数列可将三数设为 或者 ,2.)若已知 三个数成等比数列,则这三个数可设为 ,也可以设为根据具体问题的不同特点而选择不同设法。 为了便于解方程,应该充分分析条件的特征,尽量减少未知数的个数, 用最少的未知数表达出数列的有关项的数量关系,促使复杂的问题转化为较简单的问题,获得最佳的解决方法。一般地:
方法小结例2(1)已知等差数列 满足 ,则 ( )分析:C (2)已知等差数列 前 项和为30,前 项和100,则前 项和为 ( )C(4)、已知等比数列{an}中,an>0且 a2a4+2a3a5+a4a6=25,则a3+a5= ( )
(A)5 (B) 10 (C)15 (D) 20
Aa2a4=(a3)2
a4a6=(a5)2原式=(a3+a5)2=25=> a3+a5=5(an>0)提示:解法小结 掌握好等差数列、等比数列的一些常见性质并在解题中灵活运用,可以简化解题过程,起到事半功倍的效果。例3:已知数列{an}为等差数列,公差d≠0,{an}的部分项组成下列数列: 恰好为等比数列,其中k1=1,k2=5,k3=17,求k1+k2+.....+kn即得出新数列的公比:
再由∴可解出kn,进而求出根据数列{an}是等差数列,通项可写作: an=a1+(n-1)d,可表示出:a1,,a5=a1+4d,a17=a1+16d,再根据a1,a5,a17成等比数列,又可得:(a5)2=a1a17,于是可解出d=(1/2)a1.分析:1、本题是一个等差、等比数列的综合型问题,在解题过程中,分清那一步是用等差数列条件,那一步是用等比数列条件是正确解题的前提。
2。仔细观察,找到两个数列序号间的联系,是使问题得解的关键方法小结 设等差数列 {an} 的公差为d,等比数列 {bn} 的公比为 ,则由题意得解析:通项特征:由等差数列通项与等比数列通项相乘而得求和方法:错位相减法——错项法 解析: 两式相减: 错位相减法1.观察数列:30,37,32,35,34,33,36,( ),38的特点,在括号内适当的一个数是______2.在等比数列中,a4+a6=3,则a5(a3+2a5+a7)=_____3. 在等差数列{an}中,若a4+a6+a8+a10+a12=120,则
2a10-a12的值为 ( )
A.20 B.22 C.24 D.28319C4.已知数列{an}中,a1=1,并且3an+1-3an=1,则a301= ( )
A.100 B.101 C.102 D.103B5.若{an}是等比数列,且an>0,a2a4+2a3a5+a4a6=25,那
么a3+a5的值等于 ( )A.5 B.1 C.15 D.10A课堂练习:6.等差数列{an}中,已知前4项和是1,前8项和是4,则
a17+a18+a19+a20的值等于 ( )A.7 B.8 C.9 D.10C 8.在数列{an}中,a1=3,an+1=an+3n(n≥1),求此数列的通项公式.9.数列{bn}中,b1+b2+b3= ,b1b2b3= ,若{an}是等差数
列,且bn= ,求{an}的通项公式.7、四个数,前三个成等比数列,它们的和是19;后三个成等差数列,和是12,求此四个数.(四数为: 9,6,4,2或25,-10,4,18.)小 结对等差、等比综合问题
1。要正确分清题目究竟是等差还是等比,不能混淆。
2。掌握设元的技巧;
3。要掌握分析数列问题的基本思想方法,把握好等差等比数列各自的特点并在解题中灵活运用。
