4.3 一次函数的图象 湘教版数学八年级下册 课件(共25张PPT)
文档属性
| 名称 | 4.3 一次函数的图象 湘教版数学八年级下册 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-06 00:00:00 | ||
图片预览






文档简介
(共25张PPT)
4.3 一次函数的图像
湘教版数学 八年级下册
y
0
x
3
(-1,7)
(0,5)
(1,3)
(2,1)
(3,-1)
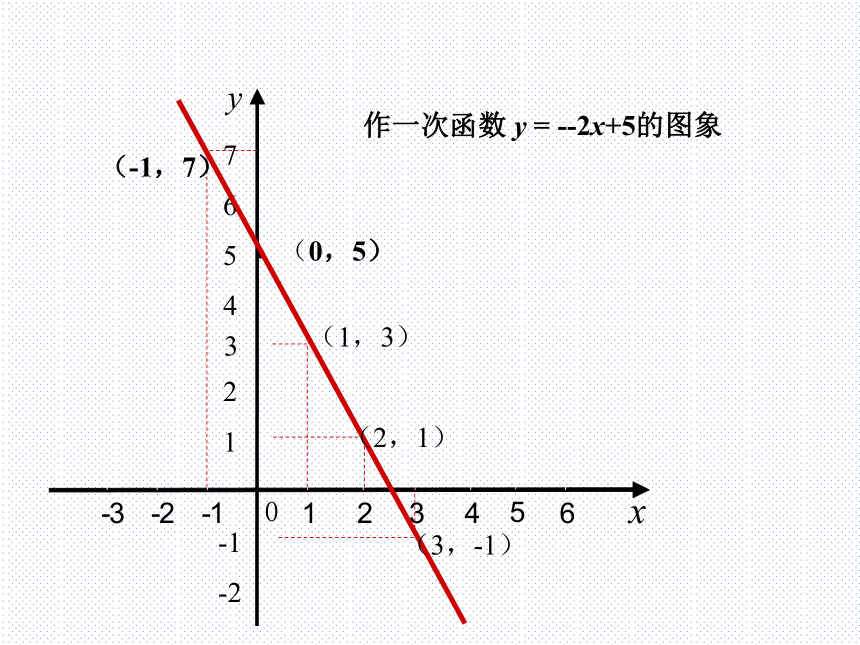
作一次函数 y = --2x+5的图象
2、 在所作的图象上取几个点,找出它们的横坐标和纵坐标,并验证它们是否满足关系y= -2x+5 ?
1、满足关系式y= -2x+5的x,y所对应的点
(x,y)都在一次函数的图象上吗?
图象上所有的点都满足关系式.
满足关系式的x,y所对应的点(x,y)都在图象上.
类似地,数学上已经证明:
一次函数y= kx+b(b≠0)的图像是一条直线.
由于两点确定一条直线,因此画一次函数的图像,只要描出图像上的两个点,然后过这两点作一条直线就行了.
我们常常把这条直线叫作“直线y= kx+b”.
1. 作出y=2x的图象?
解:列表:
…
…
y=2x
…
2
1
0
-1
-2
…
x
连线:
描点:
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
-4
-2
0
4
2
作函数图象的一般步骤:列表、描点、连线.
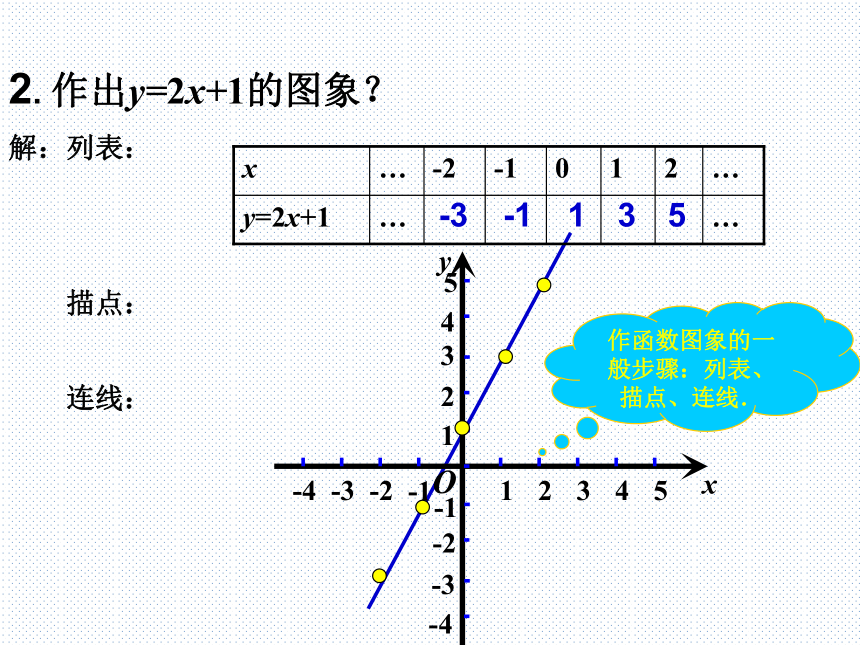
2. 作出y=2x+1的图象?
解:列表:
…
…
y=2x+1
…
2
1
0
-1
-2
…
x
连线:
描点:
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
-3
-1
1
5
3
作函数图象的一般步骤:列表、描点、连线.
从上图中,我们可以看出,对于一次函数 y=2x+1 ,当自变量 x 取的值由小变大时,对应的函数值 y 也由小变大
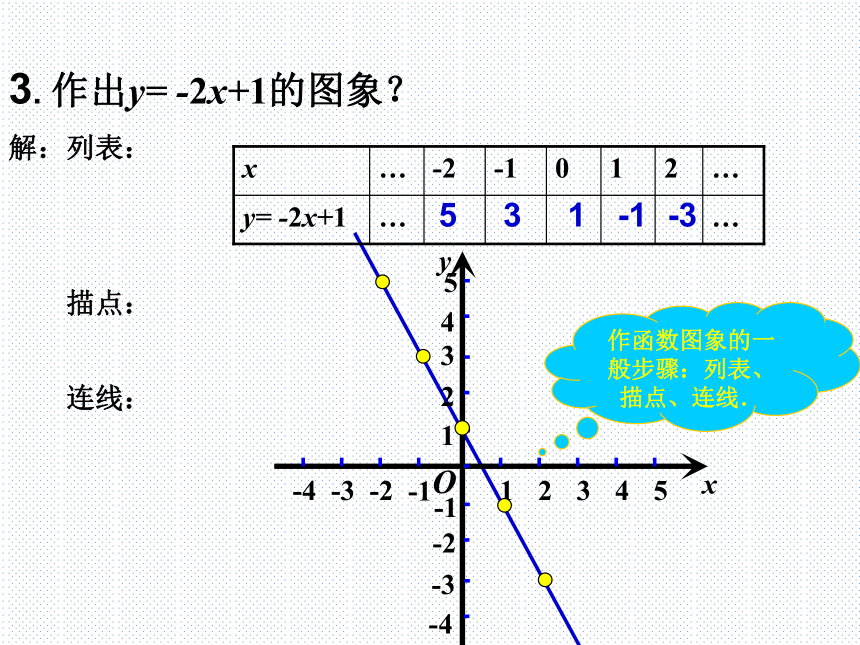
3. 作出y= -2x+1的图象?
解:列表:
…
…
y= -2x+1
…
2
1
0
-1
-2
…
x
连线:
描点:
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
5
3
1
-3
-1
作函数图象的一般步骤:列表、描点、连线.
从上图中,我们可以看出,对于一次函数 y=-2x+1 ,当自变量 x 取的值由小变大时,对应的函数值 y 反而由小变大
一次函数y= kx+b(k≠0),当k>0时,函数值随自变量的增加而增大;当k<0时,函数值随自变量的增加而减少.
从以上的两个例子中,我们可以得到:
具体的推导过程请参考课本,这个推导过程很重要,每一位同学都必须理解和掌握.
4. 请同学们在同一直角坐标系中再画出如下函数的图象:
(1)
(2)
(3)
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y=2x
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
两个一次函数,当k一样,而b不一样时,如:
与 ,
有什么共同点与不同点?
共同点:两者的图形都是直线,且互相平行;是由上面的直线向下平移2个单位长度得到的.
不同点: 经过原点(0,0),
而 与 y 轴交于点(0,2),与x轴
交于点(-4,0)
我们再来看函数 与 ,则它们又有何异同点呢?
(它们的b一样,而k不一样)
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
共同点:两者的图形都是直线,且均过点(0,2).即(0,b)
不同点: 与 x 轴交于点 (-1,0),
而 与 x 轴交于点(-4,0).
1、当两个一次函数的k一样,而b不一样,则这两个函数的图象是两条互相平行的直线,且它们之间可以通过平移得到(向上或向下),平移的距离是|b|.
2、当两个一次函数的b一样,而k不一样,则这两个函数的图象是两条相交的直线,且与y轴交于同一点,即(0,b)
对y=kx+b而言
【例 1】已知:函数 y = (m+1) x + 2 m﹣6
(1)若函数图象过(﹣1 ,2),求此函数的解析式。
(2)若函数图象与直线 y = 2 x + 5 平行,求其函数的解析式。
(3)求满足(2)条件的直线与直线 y = ﹣3 x + 1 的交点,并
求这两条直线 与y 轴所围成的三角形面积 .
解:(1)由题意:
2=﹣(m+1)+2m﹣6
解得 m = 9
(2) 由题意,m +1= 2
解得 m = 1
∴ y = 2x﹣4
(3) 由题意得
∴ 这两直线的交点是(1 ,﹣2)
y = 2x﹣4 与y 轴交于( 0 , - 4 )
y = ﹣3x + 1与y 轴交于( 0 , 1)
●
x
y
o
1
1
-4
(1, ﹣2)
S△=
-2
∴ y = 10x+12
解得:
y = 2x﹣4
y = ﹣3 x + 1
【例 2】下图 l1 l2 分别是龟兔赛跑中路程与时间之间的函数图象.
s /米
(1)这一次是 米赛跑.
1
2
3
4
5
O
100
20
120
40
60
80
t /分
6
8
7
(2)表示兔子的图象是 .
-1
12
9
10
11
-3
-2
l1
l2
100
l2
-4
根据图象可以知道:
s /米
(3)当兔子到达终点时,乌龟距终点还有 米.
l1
l2
1
2
3
4
5
O
100
20
120
40
60
80
t /分
6
8
7
(4)乌龟要与兔子同时到达终点乌龟要先跑 米.
(5)乌龟要先到达终点,至少要比兔子早跑 分钟.
-1
12
9
10
11
-3
-2
40
4
-4
40
【例 3】某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(微克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后.
x/时
y/微克
6
3
2
10
O
(1)分别求出0≤ x ≤2 和x≥2时y与x之间的函数关系式;
解:(1)当0≤ x ≤2时,
设y=kx(k≠0)
因图象过点(2,6),
代入得6=2k, k=3
∴y=3x
当x ≥ 2时, 设y=kx+b(k≠0)
因图象过点(2,6)及点(10,3),
代入得
解得
x/时
y/微克
6
3
2
10
O
(2)如果每毫升血液中含药量为4微克或4微克以上时,治疗疾病有效,那么这个有效时间是多长
当 0≤ x ≤2时, y=3x;
当x ≥ 2时,
解:
当y=4时,
由y=3x , 得
由 ,
得
所以使用该种新药的有效时间是6小时.
4
x1
x2
【例4】 (03黑龙江中考)某空军加油机接到命令,立即 给一架正在飞行的运输飞机进行空中加油,在加油过程中,设运输机的油箱余油量为Q1吨,加油飞机的加油油箱余油量为Q2吨,加油时间为t分钟,Q1、Q2与t之间的函数图像如图所示,结合图像回答下列问题:
(1)加油飞机的加油油箱中装载了多少吨油 将这些油全部加给运输飞机需多少分钟
解:(1)由图像知,加油飞机的加
油箱中装载了30吨油,全部
加给运输飞机需10分钟 ;
(2)求加油过程中,运输飞机的余油量Q1(吨)与时间t(分)的函数关系式.
解:(2)
设
因图象过点(0 , 40)及点(10 , 6 9 ),
代入得
所以 Q1=2.9t+40
(0≤t ≤10)
(3)运输飞机加完油后,以原速继续飞行,需10小时到达目的地,油料是否够用 说明理由.
解:(3)
根据图像可知
运输飞机的耗油量为每分钟0.1吨.
∴10小时耗油量为:
10×60×0.1=60吨
∴油够用.
<69吨.
4.3 一次函数的图像
湘教版数学 八年级下册
y
0
x
3
(-1,7)
(0,5)
(1,3)
(2,1)
(3,-1)
作一次函数 y = --2x+5的图象
2、 在所作的图象上取几个点,找出它们的横坐标和纵坐标,并验证它们是否满足关系y= -2x+5 ?
1、满足关系式y= -2x+5的x,y所对应的点
(x,y)都在一次函数的图象上吗?
图象上所有的点都满足关系式.
满足关系式的x,y所对应的点(x,y)都在图象上.
类似地,数学上已经证明:
一次函数y= kx+b(b≠0)的图像是一条直线.
由于两点确定一条直线,因此画一次函数的图像,只要描出图像上的两个点,然后过这两点作一条直线就行了.
我们常常把这条直线叫作“直线y= kx+b”.
1. 作出y=2x的图象?
解:列表:
…
…
y=2x
…
2
1
0
-1
-2
…
x
连线:
描点:
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
-4
-2
0
4
2
作函数图象的一般步骤:列表、描点、连线.
2. 作出y=2x+1的图象?
解:列表:
…
…
y=2x+1
…
2
1
0
-1
-2
…
x
连线:
描点:
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
-3
-1
1
5
3
作函数图象的一般步骤:列表、描点、连线.
从上图中,我们可以看出,对于一次函数 y=2x+1 ,当自变量 x 取的值由小变大时,对应的函数值 y 也由小变大
3. 作出y= -2x+1的图象?
解:列表:
…
…
y= -2x+1
…
2
1
0
-1
-2
…
x
连线:
描点:
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
5
3
1
-3
-1
作函数图象的一般步骤:列表、描点、连线.
从上图中,我们可以看出,对于一次函数 y=-2x+1 ,当自变量 x 取的值由小变大时,对应的函数值 y 反而由小变大
一次函数y= kx+b(k≠0),当k>0时,函数值随自变量的增加而增大;当k<0时,函数值随自变量的增加而减少.
从以上的两个例子中,我们可以得到:
具体的推导过程请参考课本,这个推导过程很重要,每一位同学都必须理解和掌握.
4. 请同学们在同一直角坐标系中再画出如下函数的图象:
(1)
(2)
(3)
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y=2x
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
两个一次函数,当k一样,而b不一样时,如:
与 ,
有什么共同点与不同点?
共同点:两者的图形都是直线,且互相平行;是由上面的直线向下平移2个单位长度得到的.
不同点: 经过原点(0,0),
而 与 y 轴交于点(0,2),与x轴
交于点(-4,0)
我们再来看函数 与 ,则它们又有何异同点呢?
(它们的b一样,而k不一样)
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
共同点:两者的图形都是直线,且均过点(0,2).即(0,b)
不同点: 与 x 轴交于点 (-1,0),
而 与 x 轴交于点(-4,0).
1、当两个一次函数的k一样,而b不一样,则这两个函数的图象是两条互相平行的直线,且它们之间可以通过平移得到(向上或向下),平移的距离是|b|.
2、当两个一次函数的b一样,而k不一样,则这两个函数的图象是两条相交的直线,且与y轴交于同一点,即(0,b)
对y=kx+b而言
【例 1】已知:函数 y = (m+1) x + 2 m﹣6
(1)若函数图象过(﹣1 ,2),求此函数的解析式。
(2)若函数图象与直线 y = 2 x + 5 平行,求其函数的解析式。
(3)求满足(2)条件的直线与直线 y = ﹣3 x + 1 的交点,并
求这两条直线 与y 轴所围成的三角形面积 .
解:(1)由题意:
2=﹣(m+1)+2m﹣6
解得 m = 9
(2) 由题意,m +1= 2
解得 m = 1
∴ y = 2x﹣4
(3) 由题意得
∴ 这两直线的交点是(1 ,﹣2)
y = 2x﹣4 与y 轴交于( 0 , - 4 )
y = ﹣3x + 1与y 轴交于( 0 , 1)
●
x
y
o
1
1
-4
(1, ﹣2)
S△=
-2
∴ y = 10x+12
解得:
y = 2x﹣4
y = ﹣3 x + 1
【例 2】下图 l1 l2 分别是龟兔赛跑中路程与时间之间的函数图象.
s /米
(1)这一次是 米赛跑.
1
2
3
4
5
O
100
20
120
40
60
80
t /分
6
8
7
(2)表示兔子的图象是 .
-1
12
9
10
11
-3
-2
l1
l2
100
l2
-4
根据图象可以知道:
s /米
(3)当兔子到达终点时,乌龟距终点还有 米.
l1
l2
1
2
3
4
5
O
100
20
120
40
60
80
t /分
6
8
7
(4)乌龟要与兔子同时到达终点乌龟要先跑 米.
(5)乌龟要先到达终点,至少要比兔子早跑 分钟.
-1
12
9
10
11
-3
-2
40
4
-4
40
【例 3】某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(微克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后.
x/时
y/微克
6
3
2
10
O
(1)分别求出0≤ x ≤2 和x≥2时y与x之间的函数关系式;
解:(1)当0≤ x ≤2时,
设y=kx(k≠0)
因图象过点(2,6),
代入得6=2k, k=3
∴y=3x
当x ≥ 2时, 设y=kx+b(k≠0)
因图象过点(2,6)及点(10,3),
代入得
解得
x/时
y/微克
6
3
2
10
O
(2)如果每毫升血液中含药量为4微克或4微克以上时,治疗疾病有效,那么这个有效时间是多长
当 0≤ x ≤2时, y=3x;
当x ≥ 2时,
解:
当y=4时,
由y=3x , 得
由 ,
得
所以使用该种新药的有效时间是6小时.
4
x1
x2
【例4】 (03黑龙江中考)某空军加油机接到命令,立即 给一架正在飞行的运输飞机进行空中加油,在加油过程中,设运输机的油箱余油量为Q1吨,加油飞机的加油油箱余油量为Q2吨,加油时间为t分钟,Q1、Q2与t之间的函数图像如图所示,结合图像回答下列问题:
(1)加油飞机的加油油箱中装载了多少吨油 将这些油全部加给运输飞机需多少分钟
解:(1)由图像知,加油飞机的加
油箱中装载了30吨油,全部
加给运输飞机需10分钟 ;
(2)求加油过程中,运输飞机的余油量Q1(吨)与时间t(分)的函数关系式.
解:(2)
设
因图象过点(0 , 40)及点(10 , 6 9 ),
代入得
所以 Q1=2.9t+40
(0≤t ≤10)
(3)运输飞机加完油后,以原速继续飞行,需10小时到达目的地,油料是否够用 说明理由.
解:(3)
根据图像可知
运输飞机的耗油量为每分钟0.1吨.
∴10小时耗油量为:
10×60×0.1=60吨
∴油够用.
<69吨.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
