锐角三角函数复习题目[下学期]
图片预览



文档简介
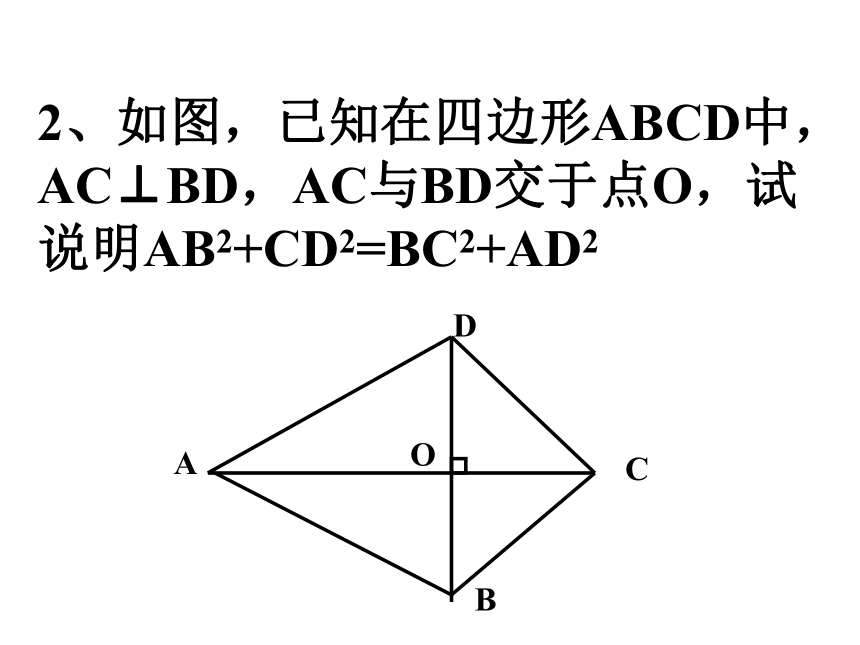
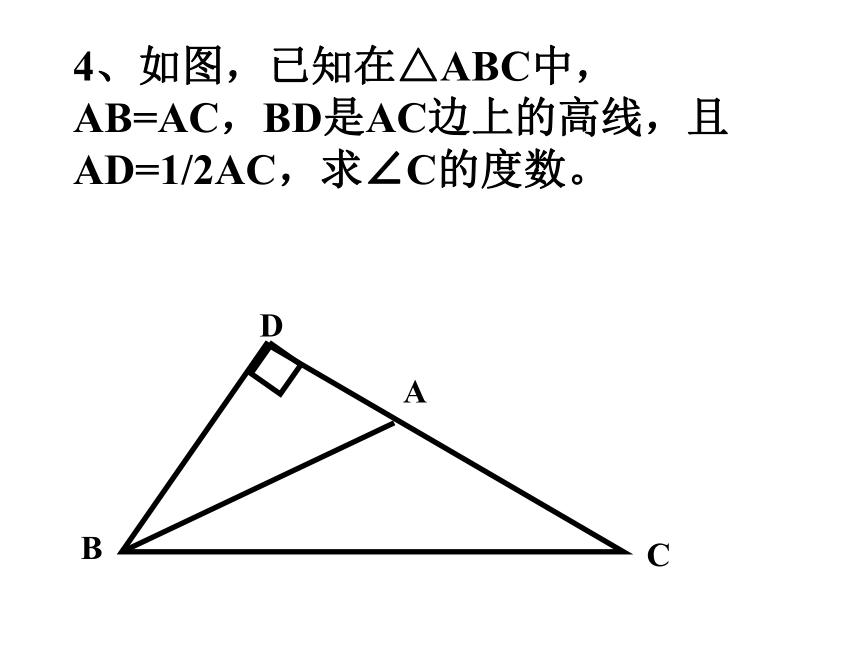
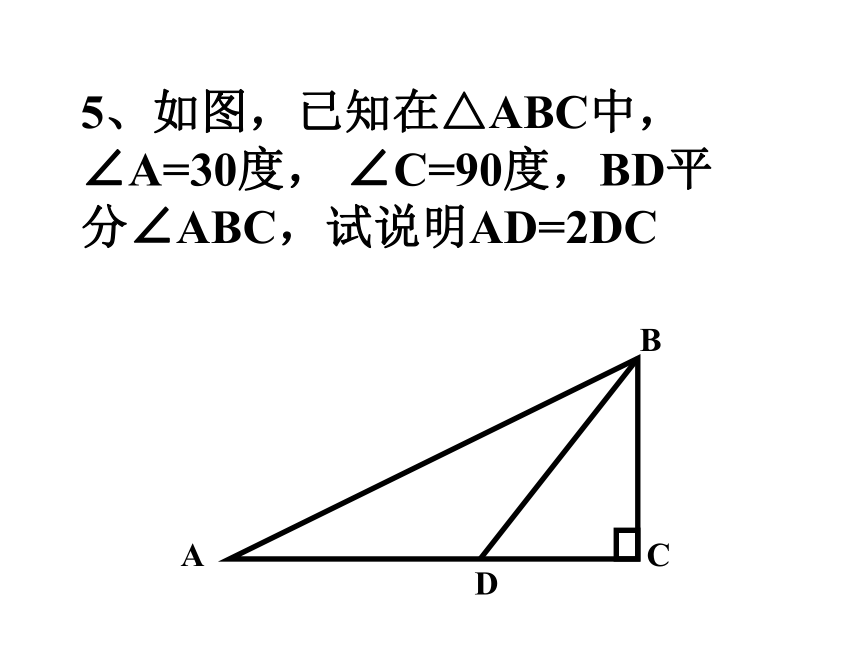
课件13张PPT。1、已知三角形的两边长分别为4和5,第三边上的高线长为3,试求此三角形的面积。2、如图,已知在四边形ABCD中,AC⊥BD,AC与BD交于点O,试说明AB2+CD2=BC2+AD2ACBDO3、如图,已知在△ABC中,∠A=90度,P是AC中点,PD⊥BC,D是垂足,BC=9,DC=3,求AB的长。ACBPD4、如图,已知在△ABC中,AB=AC,BD是AC边上的高线,且AD=1/2AC,求∠C的度数。ACBD5、如图,已知在△ABC中,∠A=30度, ∠C=90度,BD平分∠ABC,试说明AD=2DCACBD6、在Rt△ABC中,∠C=90度,sinA+cosB= ,求∠A的度数。7、如图,已知在矩形ABCD中,点E在BC边上,且∠AEB=30度,∠CDE=15度,请探索线段AD与CD之间的数量关系,并说明你的猜想。ADCBE9、在△ABC中,AD是BC边上的高线,tanB=cos∠DAC,
(1)试说明:AC =BD.
(2)若sinC=12/13,BC=12,求AD的长。ACBD8、如图,已知在△ABC中,∠B=45度,D是BC延长线上的一点,AD= ,AC=DC=3,求∠ADC的度数及AB的长。ADCB11、如图,已知在Rt△ABC中,∠ACB=90度, CD是中线,P是CD上一点(P与C,D可以重合),BC=5,AC=12.
(1)若设CP=x,S△ACP=y,写出y与x 之间的函数关系式,并指出x的取值范围。
(2)求当y=10时,cos∠PAC的值。ACBDP10、在△ABC中,∠ABC=135度,P是AC上一点,且∠PBA=90度,CP/PA=1/2,
(1)求tan ∠APB的值;
(2)若PB=2,求AC的长APCB12、边长为8和4的矩形OABC的两边分别在直角坐标系的X轴和Y轴上,若 沿对角线AC折叠后,点B落在第四象限B1处,设B1C交X轴于点D,求(1)三角形ADC的面积,(2)点B1的坐标,(3)AB1所在的直线解析式。OCBAB1D123E13、直线y=0.75x+3与x轴y轴的交点分别是A和B,点C在x轴上,且ABC构成等腰三角形,求C的坐标,
(1)试说明:AC =BD.
(2)若sinC=12/13,BC=12,求AD的长。ACBD8、如图,已知在△ABC中,∠B=45度,D是BC延长线上的一点,AD= ,AC=DC=3,求∠ADC的度数及AB的长。ADCB11、如图,已知在Rt△ABC中,∠ACB=90度, CD是中线,P是CD上一点(P与C,D可以重合),BC=5,AC=12.
(1)若设CP=x,S△ACP=y,写出y与x 之间的函数关系式,并指出x的取值范围。
(2)求当y=10时,cos∠PAC的值。ACBDP10、在△ABC中,∠ABC=135度,P是AC上一点,且∠PBA=90度,CP/PA=1/2,
(1)求tan ∠APB的值;
(2)若PB=2,求AC的长APCB12、边长为8和4的矩形OABC的两边分别在直角坐标系的X轴和Y轴上,若 沿对角线AC折叠后,点B落在第四象限B1处,设B1C交X轴于点D,求(1)三角形ADC的面积,(2)点B1的坐标,(3)AB1所在的直线解析式。OCBAB1D123E13、直线y=0.75x+3与x轴y轴的交点分别是A和B,点C在x轴上,且ABC构成等腰三角形,求C的坐标,
