2022—2023学年华东师大版数学九年级上册24.4解直角三角形复习 课件(共16张PPT)
文档属性
| 名称 | 2022—2023学年华东师大版数学九年级上册24.4解直角三角形复习 课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 407.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-06 08:50:48 | ||
图片预览


文档简介
(共16张PPT)
1
华东师大版《数学 · 九年级(上)》
第一课时
§24.解直角三角形
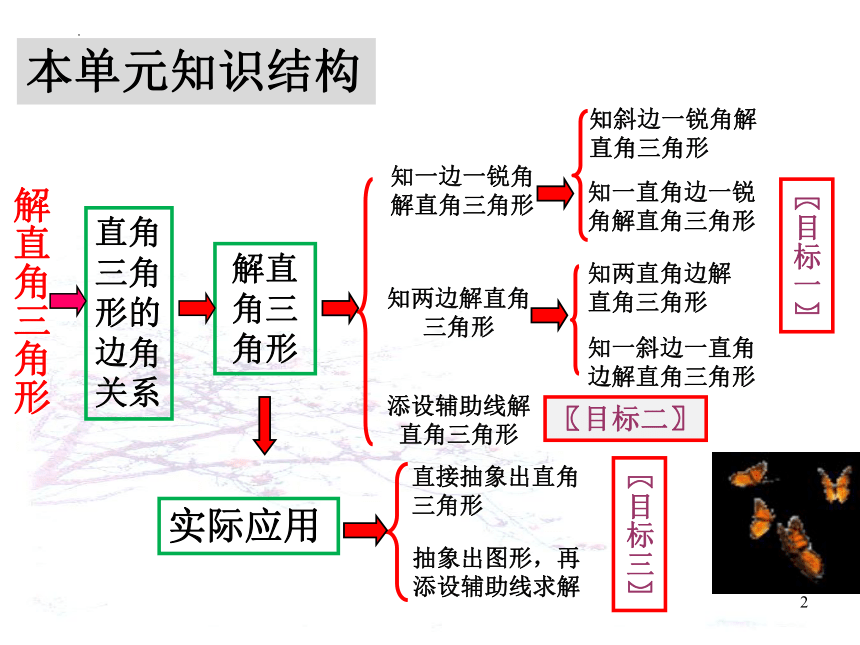
本单元知识结构
直角三角形的边角关系
解直 角三角形
知一边一锐角解直角三角形
知两边解直角三角形
添设辅助线解直角三角形
知斜边一锐角解直角三角形
知一直角边一锐角解直角三角形
知两直角边解直角三角形
知一斜边一直角边解直角三角形
实际应用
抽象出图形,再添设辅助线求解
直接抽象出直角三角形
解直角三角形
〖目标一〗
〖目标二〗
〖目标三〗
2
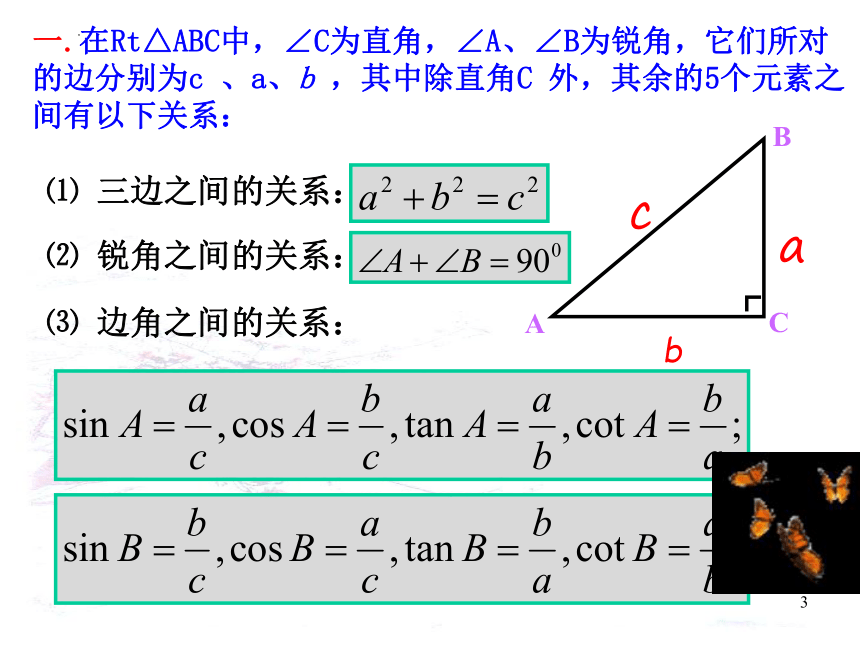
一.在Rt△ABC中,∠C为直角,∠A、∠B为锐角,它们所对的边分别为c 、a、b ,其中除直角C 外,其余的5个元素之间有以下关系:
⑴ 三边之间的关系:
⑵ 锐角之间的关系:
⑶ 边角之间的关系:
A
B
b
a
c
┏
C
3
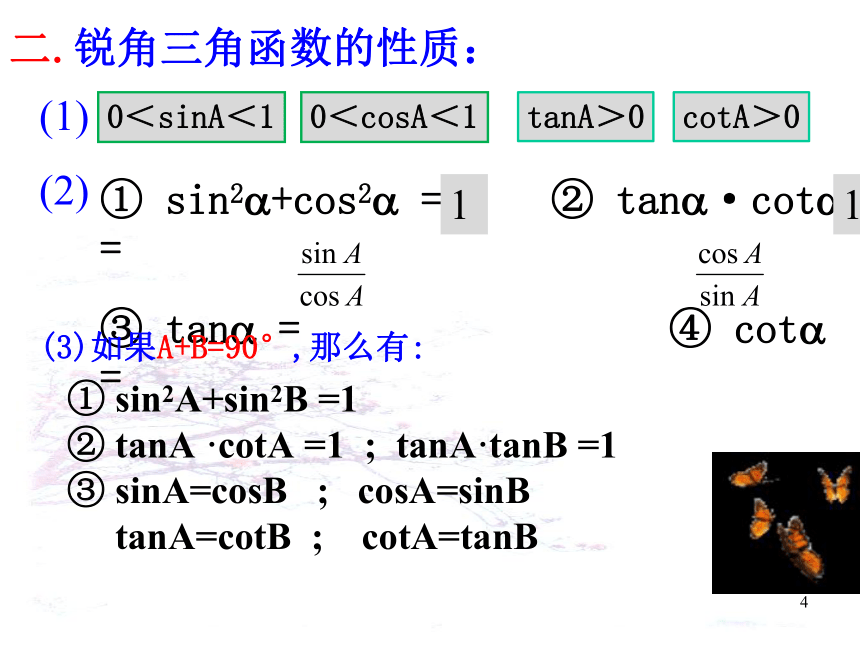
二.锐角三角函数的性质:
0<sinA<1
0<cosA<1
tanA>0
cotA>0
(1)
① sin2 +cos2 = ② tan ·cot =
③ tan = ④ cot =
1
1
(2)
(3)如果A+B=90°,那么有:
① sin2A+sin2B =1
② tanA ·cotA =1 ; tanA·tanB =1
③ sinA=cosB ; cosA=sinB
tanA=cotB ; cotA=tanB
4
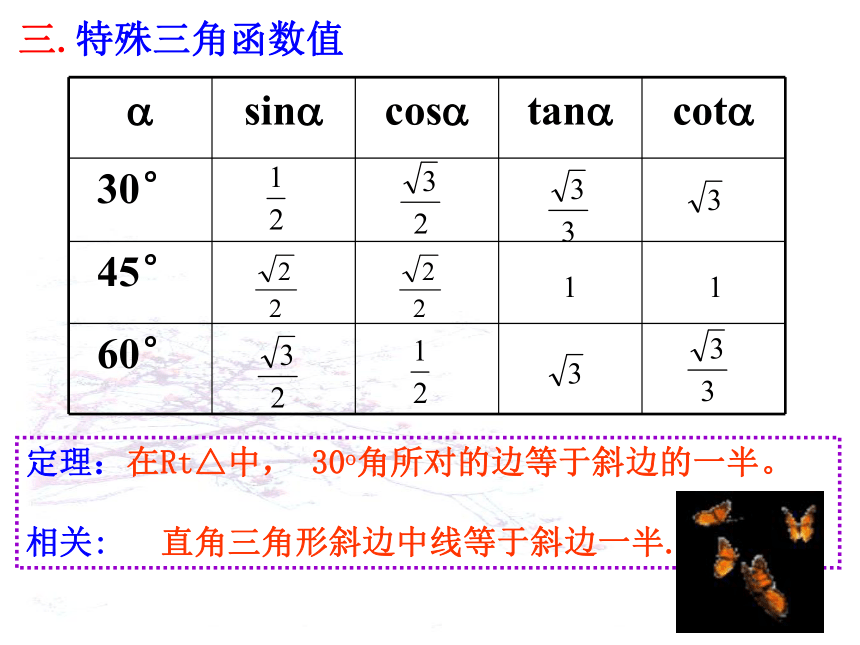
三.特殊三角函数值
sin cos tan cot
30°
45°
60°
定理:在Rt△中, 30o角所对的边等于斜边的一半。
相关: 直角三角形斜边中线等于斜边一半.
5
3.在Rt△ABC中,∠C=90°,根据下列条件,求角A。
基础练习
)
____(精确到1
C
3.126,则
若cotC
效数字)
____(保留四个有
45
1.若cos23
’
'
o
=
=
=
6
1.在直角三角形中,我们把两个锐角、三条边称为直角三角形的五个元素.图中∠A,∠B,a,b,c即为直角三角形的五个元素.
2.解直角三角形:在直角三角形中,由已知元素求未知元素的过程,叫做解直角三角形.
A
B
a
b
c
C
四.解直角三角形
3.解直角三
角形类型
已知两边长
已知一个锐
角和一边长
→
→
勾股定理、 三角函数
(求边长) (求角度)
三角函数、 两角互余
(求边长) (求角度)
注意:
1.在初中研究的是锐角的三角函数,都是在直角三角形中定义的,而锐角三角函数值的大小与所在的三角形无关,只与角本身大小有关。
2.利用三角函数的定义求值时如果图形中没有直角三角形,首先要添加辅助线构造直角三角形
7
练习:
1.在Rt△ABC中,∠C=90°,解此直角三角形。
①.∠A=60°,c=8,则a=______,b=____.
②.a=2,cosA= ,c=___.
③.sinA= ,则tanB=_____.
2. 在□ABCD中AB=6 ,BC=8,∠B=60°求平行四边形的的面积
A
B
C
D
┓
E
3.如图,在△ABC中,AC=6,∠A=60°,∠B=45°,求S△ABC.
A
C
┓
D
B
⌒
450
⌒
60°
6
8
4
3
9
华东师大版《数学 · 九年级(上)》
第二课时
§24.解直角三角形的实践应用
仰角
俯角
目标C
方位角
h
l
α
i=h:l
视线A
视线B
水平线
五.直角三角形的应用
1.在直角三角形的应用中,常常涉及到的概念有仰角、俯角、方位角、坡度、坡角等。
坡角
2.解直角三角形的步骤:
1.弄清其中名词的概念,根据题意画出几何图形;
2.把实际问题转化为数学问题,建立数学模型;
3.找到基本三角形,添加辅助线,构造直角三角形,利用三角函数找到边角之间的关系,选择合适的三角关系求解;
4.按题目中已知数的精确度进行近似计算,按要求的精确度确定答案及单位。
10
B
E
例1:如图,某幢大楼顶部有一块广告牌CD,甲、乙两人分别在相距8米的A、B两处测得D点和C点的仰角分别为45°和60°,且A、B、E三点在一条直线上。若BE=15米,求这块广告牌的高度。(精确到1米)
专题:仰角与俯角应用
解:根据题意可得:
AB=8,BE=15,∠DAE=45°,∠CBE= 60°
∴AE=23
在Rt△AED中,∠DAE=45°
∴DE=AE=23
在Rt△BEC中,∠CBE= 60°
∴CE=BE×tan60°=
∴CD=CE-DE=
即这块广告牌的高度约为3米
11
例2:在一次活动课上,老师带领学生去测一条河流的宽度(如图),有个同学在河岸点A处观测到河流对岸岸边有一点C,测得C在点A东偏北29度的方向上,沿河岸前行30米到达B处,测得C在点B东偏北45度方向上,请你根据以上数据,求出这条河流的宽度
参考数据: )
D
30米
专题:方位角的应用
解:如图,过点C作CD⊥AB,垂足为D,设CD=x.
在Rt△BDC中,∠CBD=45°
∴BD=CD=x
在Rt△ACD中,因∠CAD=29°
∴CD/AD=tan∠CAD=tan29 °=3/5,
而AD=AB+BD=30+x,
解得:x=45.
答:河宽45米.
12
例3.如图,一段河坝的断面如梯形ABCD,试根据图中数据,求出坡角 和坝底宽AD .(iCD=1: ,结果保留根号,单位米)
A F E D
B 3 C
5 4
专题:坡角与坡度的应用
13
1.作高线可以把锐角三角形或钝角三角形转化为两个直角三角形.
2.作高线可以把平行四边形、梯形转化为含直角三角形的图形.
六.作辅助线分割图形
3.连线割补,可以把不规则四边形转化为含直角三角形的图形.
14
本单元知识结构
直角三角形的边角关系
解直 角三角形
知一边一锐角解直角三角形
知两边解直角三角形
添设辅助线解直角三角形
知斜边一锐角解直角三角形
知一直角边一锐角解直角三角形
知两直角边解直角三角形
知一斜边一直角边解直角三角形
实际应用
抽象出图形,再添设辅助线求解
直接抽象出直角三角形
解直角三角形
〖目标一〗
〖目标二〗
〖目标三〗
15
作业
1.课本P117页第3、4、题做作业本上;
2.课本P120页复习题做在教材相应的位置上;
16
1
华东师大版《数学 · 九年级(上)》
第一课时
§24.解直角三角形
本单元知识结构
直角三角形的边角关系
解直 角三角形
知一边一锐角解直角三角形
知两边解直角三角形
添设辅助线解直角三角形
知斜边一锐角解直角三角形
知一直角边一锐角解直角三角形
知两直角边解直角三角形
知一斜边一直角边解直角三角形
实际应用
抽象出图形,再添设辅助线求解
直接抽象出直角三角形
解直角三角形
〖目标一〗
〖目标二〗
〖目标三〗
2
一.在Rt△ABC中,∠C为直角,∠A、∠B为锐角,它们所对的边分别为c 、a、b ,其中除直角C 外,其余的5个元素之间有以下关系:
⑴ 三边之间的关系:
⑵ 锐角之间的关系:
⑶ 边角之间的关系:
A
B
b
a
c
┏
C
3
二.锐角三角函数的性质:
0<sinA<1
0<cosA<1
tanA>0
cotA>0
(1)
① sin2 +cos2 = ② tan ·cot =
③ tan = ④ cot =
1
1
(2)
(3)如果A+B=90°,那么有:
① sin2A+sin2B =1
② tanA ·cotA =1 ; tanA·tanB =1
③ sinA=cosB ; cosA=sinB
tanA=cotB ; cotA=tanB
4
三.特殊三角函数值
sin cos tan cot
30°
45°
60°
定理:在Rt△中, 30o角所对的边等于斜边的一半。
相关: 直角三角形斜边中线等于斜边一半.
5
3.在Rt△ABC中,∠C=90°,根据下列条件,求角A。
基础练习
)
____(精确到1
C
3.126,则
若cotC
效数字)
____(保留四个有
45
1.若cos23
’
'
o
=
=
=
6
1.在直角三角形中,我们把两个锐角、三条边称为直角三角形的五个元素.图中∠A,∠B,a,b,c即为直角三角形的五个元素.
2.解直角三角形:在直角三角形中,由已知元素求未知元素的过程,叫做解直角三角形.
A
B
a
b
c
C
四.解直角三角形
3.解直角三
角形类型
已知两边长
已知一个锐
角和一边长
→
→
勾股定理、 三角函数
(求边长) (求角度)
三角函数、 两角互余
(求边长) (求角度)
注意:
1.在初中研究的是锐角的三角函数,都是在直角三角形中定义的,而锐角三角函数值的大小与所在的三角形无关,只与角本身大小有关。
2.利用三角函数的定义求值时如果图形中没有直角三角形,首先要添加辅助线构造直角三角形
7
练习:
1.在Rt△ABC中,∠C=90°,解此直角三角形。
①.∠A=60°,c=8,则a=______,b=____.
②.a=2,cosA= ,c=___.
③.sinA= ,则tanB=_____.
2. 在□ABCD中AB=6 ,BC=8,∠B=60°求平行四边形的的面积
A
B
C
D
┓
E
3.如图,在△ABC中,AC=6,∠A=60°,∠B=45°,求S△ABC.
A
C
┓
D
B
⌒
450
⌒
60°
6
8
4
3
9
华东师大版《数学 · 九年级(上)》
第二课时
§24.解直角三角形的实践应用
仰角
俯角
目标C
方位角
h
l
α
i=h:l
视线A
视线B
水平线
五.直角三角形的应用
1.在直角三角形的应用中,常常涉及到的概念有仰角、俯角、方位角、坡度、坡角等。
坡角
2.解直角三角形的步骤:
1.弄清其中名词的概念,根据题意画出几何图形;
2.把实际问题转化为数学问题,建立数学模型;
3.找到基本三角形,添加辅助线,构造直角三角形,利用三角函数找到边角之间的关系,选择合适的三角关系求解;
4.按题目中已知数的精确度进行近似计算,按要求的精确度确定答案及单位。
10
B
E
例1:如图,某幢大楼顶部有一块广告牌CD,甲、乙两人分别在相距8米的A、B两处测得D点和C点的仰角分别为45°和60°,且A、B、E三点在一条直线上。若BE=15米,求这块广告牌的高度。(精确到1米)
专题:仰角与俯角应用
解:根据题意可得:
AB=8,BE=15,∠DAE=45°,∠CBE= 60°
∴AE=23
在Rt△AED中,∠DAE=45°
∴DE=AE=23
在Rt△BEC中,∠CBE= 60°
∴CE=BE×tan60°=
∴CD=CE-DE=
即这块广告牌的高度约为3米
11
例2:在一次活动课上,老师带领学生去测一条河流的宽度(如图),有个同学在河岸点A处观测到河流对岸岸边有一点C,测得C在点A东偏北29度的方向上,沿河岸前行30米到达B处,测得C在点B东偏北45度方向上,请你根据以上数据,求出这条河流的宽度
参考数据: )
D
30米
专题:方位角的应用
解:如图,过点C作CD⊥AB,垂足为D,设CD=x.
在Rt△BDC中,∠CBD=45°
∴BD=CD=x
在Rt△ACD中,因∠CAD=29°
∴CD/AD=tan∠CAD=tan29 °=3/5,
而AD=AB+BD=30+x,
解得:x=45.
答:河宽45米.
12
例3.如图,一段河坝的断面如梯形ABCD,试根据图中数据,求出坡角 和坝底宽AD .(iCD=1: ,结果保留根号,单位米)
A F E D
B 3 C
5 4
专题:坡角与坡度的应用
13
1.作高线可以把锐角三角形或钝角三角形转化为两个直角三角形.
2.作高线可以把平行四边形、梯形转化为含直角三角形的图形.
六.作辅助线分割图形
3.连线割补,可以把不规则四边形转化为含直角三角形的图形.
14
本单元知识结构
直角三角形的边角关系
解直 角三角形
知一边一锐角解直角三角形
知两边解直角三角形
添设辅助线解直角三角形
知斜边一锐角解直角三角形
知一直角边一锐角解直角三角形
知两直角边解直角三角形
知一斜边一直角边解直角三角形
实际应用
抽象出图形,再添设辅助线求解
直接抽象出直角三角形
解直角三角形
〖目标一〗
〖目标二〗
〖目标三〗
15
作业
1.课本P117页第3、4、题做作业本上;
2.课本P120页复习题做在教材相应的位置上;
16
