锐角三角函数复习[下学期]

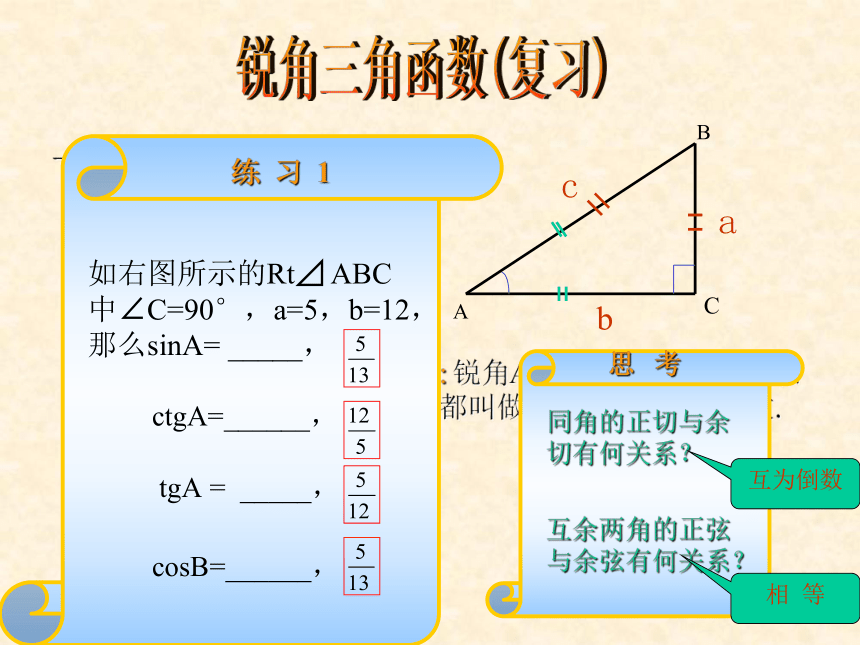
课件14张PPT。韩 民韩 民锐角三角函数复习锐角三角函数(复习)一、基本概念1.正弦ABCacsinA=2.余弦bcosA=3.正切tgA=4.余切ctgA= 锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数.定义:如右图所示的Rt⊿ ABC中∠C=90°，a=5，b=12，那么sinA= _____，ctgA=______， tgA = _____，cosB=______，同角的正切与余切有何关系？互余两角的正弦与余弦有何关系？互为倒数相 等互余两个角的三角函数关系二、几个重要关系式锐角三角函数(复习)条件：∠A为锐角
tgA·ctgA=1同角的正切余互为倒数sinA=cos（90°- A ）
cosA=sin（90°- A）
tgA =ctg（90°- A）
ctgA= tg（90°- A）同角的正弦余弦平方和等于1sin2A+cos2A=1⑴ 已知角A为锐角，且tgA=0.6，则ctgA=( ).0.6⑵ sin2A+tgActgA - 2 +
cos2A=( ).0⑶ tg44°ctg46°= ( ).1思考：
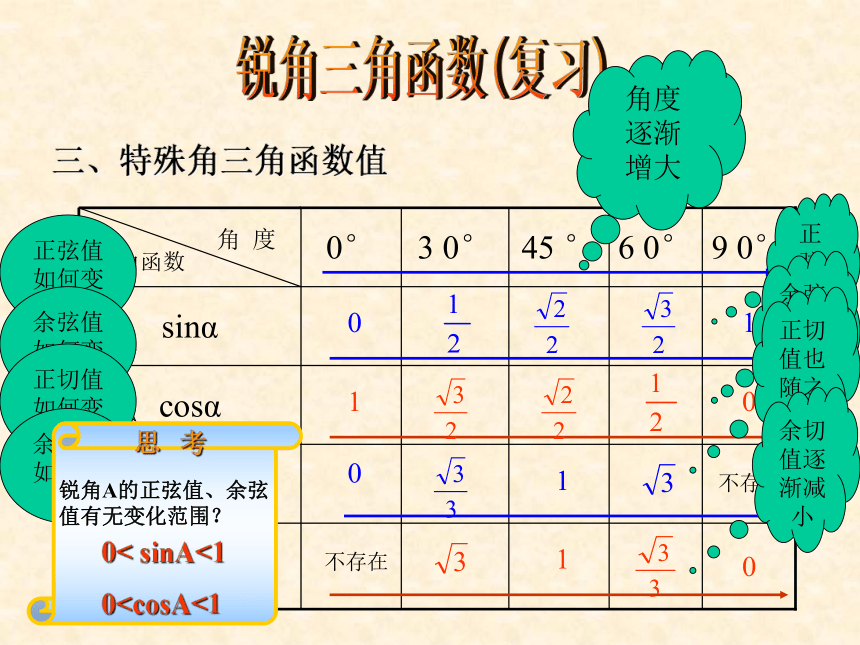
tg29°tg60°tg61°=( ).锐角三角函数(复习)三、特殊角三角函数值10011100不存在不存在角度
逐渐
增大正弦值如何变化?正弦值也增大余弦值如何变化?余弦值逐渐减小正切值如何变化?正切值也随之增大余切值如何变化?余切值逐渐减小锐角A的正弦值、余弦值有无变化范围？0< sinA<1
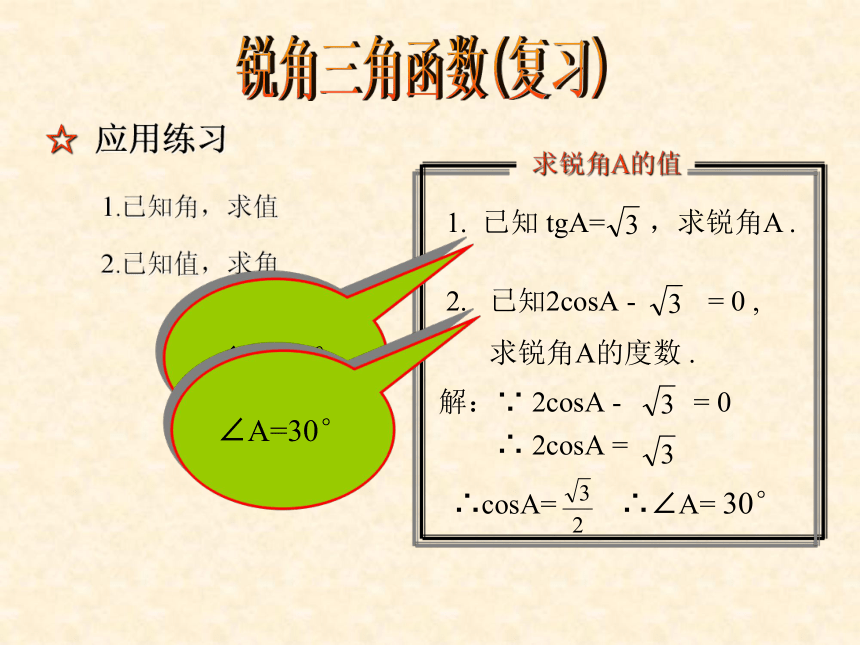
045°时，sinA的值（ ）B2. 当锐角A>30°时，cosA的值（ ）C锐角三角函数(复习)☆ 应用练习1.已知角，求值2.已知值，求角3. 确定值的范围(A)小于30° (B)大于30°
(C) 小于60° (D)大于60°B4. 确定角的范围(A)小于30° (B)大于30°
(C) 小于60° (D)大于60°B锐角三角函数(复习)☆ 应用练习1.已知角，求值2.已知值，求角3. 确定值的范围4. 确定角的范围(A)0°＜∠A≤ 30 ° (B) 30°＜∠A≤45°
(C)45°＜∠A≤ 60 ° (D) 60°＜∠A≤ 90 ° (A)0°＜∠A≤ 30 ° (B) 30°＜∠A≤45°
(C)45°＜∠A≤ 60 ° (D) 60°＜∠A≤ 90 ° DA锐角三角函数(复习)一、基本概念三、特殊角三角函数值特殊角的三角函数值(A)小于30° (B)大于30°
(C) 小于60° (D)大于60°B特殊角的三角函数值(A)小于30° (B)大于30°
(C) 小于60° (D)大于60°注意：余切值随着角度增大而减小！B特殊角的三角函数值(A)0°＜∠A≤ 30 ° (B) 30°＜∠A≤45°
(C)45°＜∠A≤ 60 ° (D) 60°＜∠A≤ 90 ° D谢谢同学们的精彩表现再见