锐角三角函数(1)[上学期]
图片预览





文档简介
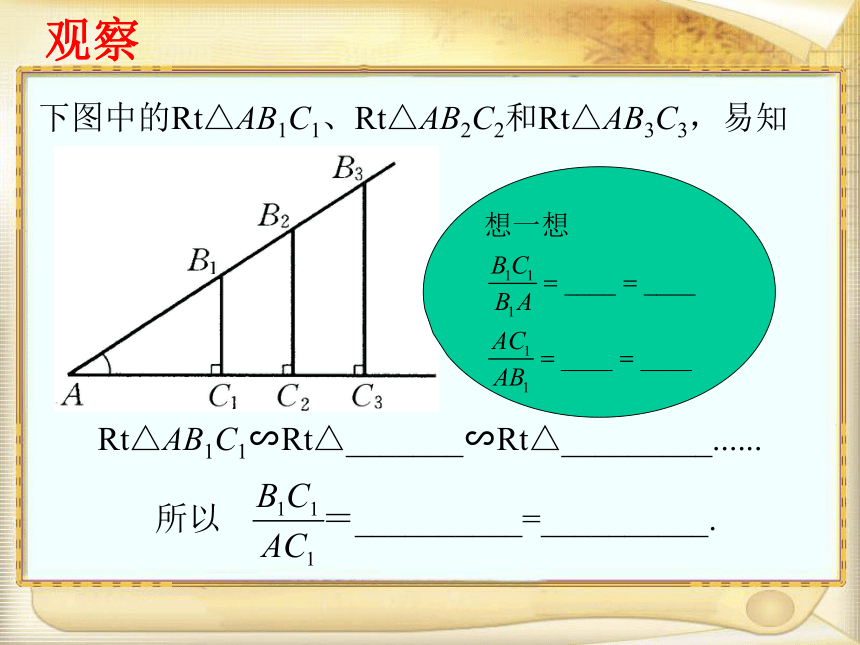
课件17张PPT。锐角三角函数(1)下图中的Rt△AB1C1、Rt△AB2C2和Rt△AB3C3,易知
Rt△AB1C1∽Rt△_______∽Rt△_________......
所以 =__________=__________. 观察想一想
一般情况下,在Rt△ABC中,当锐角A取固定值时,∠A的对边与邻边的比值是一个固定值的吗?
∠A的对边与斜边的比值是一个固定值的吗?
∠A的邻边与斜边的比值是一个固定值的吗?
思 考在Rt△ABC中,对于锐角A的每一个确定的值,其对边与邻边的比值是惟一确定的.
概括 我们同样可以发现,对于锐角A的每一个确定的值,其对边与斜边、邻边与斜边、邻边与对边的比值也是惟一确定的. 因此这几个比值都是锐角∠A的函数,
记作sin A、cos A、tan A、cot A 正弦:sin A= ,
余弦:cos A= ,
正切:tan A= ,
余切:cot A= .
锐角三角函数的定义
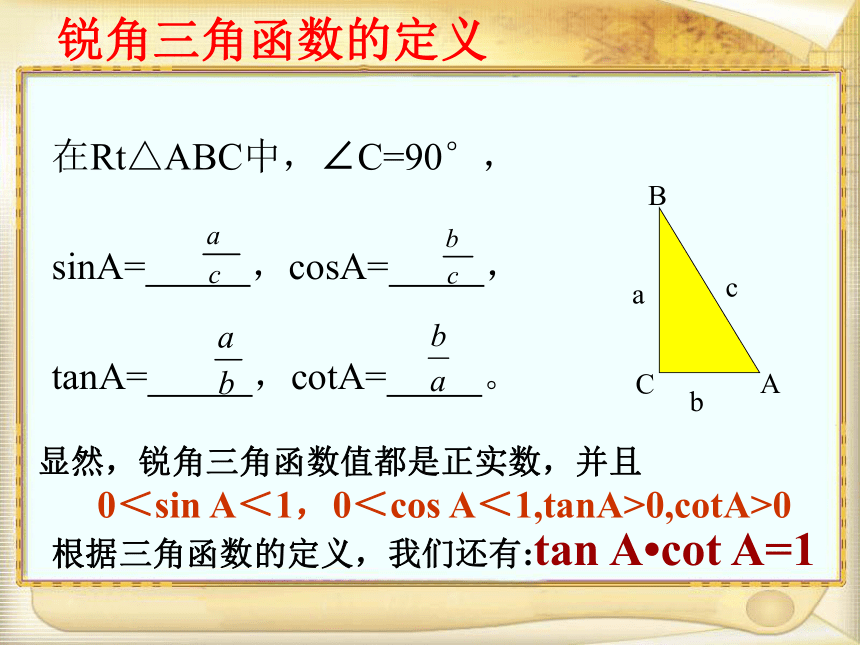
锐角三角函数的定义在Rt△ABC中,∠C=90°,
sinA= ,cosA= ,
tanA= ,cotA= 。 显然,锐角三角函数值都是正实数,并且
0<sin A<1,0<cos A<1,tanA>0,cotA>0根据三角函数的定义,我们还有:tan A?cot A=1锐角三角函数的定义注意2.sinA,cosA,tanA,cotA都是整体符号,不能看成sin·A,cos · A,tan · A,cot · A1.当角A固定时,它的三角函数值都是固定的,与角A的边长短无关3.若用三个大写字母表示一个角时,在表示它的三角函数时,角的符号“∠”不能省略.例: 1.如图,在Rt△MNP中,∠N=90゜.
∠P的对边是________,∠P的邻边是______;
∠M的对边是_______,∠M的邻边是______; 试一试2.求出如图所示的Rt△DEC(∠E=90゜)中∠D的四个三角函数值. 试一试1.在Rt△ABC中,∠C=90°,sinA= , 求∠B的四个三角函数值。分析 在直角三角形中,给出锐角的任何一个三角函数值都等于给出两条边长的比,若其中一条边长已知,就可求出另一条边长;若两边都未给出,则可考虑设辅助未知数。解 在Rt△ABC中,由sinA=
可设BC=4k,AB=5k,k≠0则
有AC=
∴sinB= ,cosB=
tanB= ,cotB=例 题2.如图,在Rt△ABC中,∠ACB=90°, BC=5,AC=4, (1)求sinA ,sinB的值, (2)过点C作CD⊥AB,求cos∠ACD.例 题3.在等腰△ABC中,AB=AC=13,BC=10,
求tanB,cotC.例 题求锐角三角函数时,勾股定理的运用是很重要的.基础练习1.在△ABC中,∠C=90°,BC=3,tanB=
则AB= 。
2.在△ABC中,∠C=90°,如果tanA= ,那么sinB=( )。
A B C D
3.在△ABC中,已知AC=3,BC=4,AB=5,那么下列结论成立的是( )。
A sinA= B cosA=
C tanA= D cotA=4.如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定5.已知∠A,∠B为锐角
(1)若∠A=∠B,则tanA tanB;
(2)若tanA=tanB,则∠A ∠B.基础练习 6.sinA=2m-3(A为锐角),则m的取值范围是___.在Rt△ABC中,∠C=90°,
sinA= ,cosA= ,
tanA= ,cotA= 。 (1)0<sin A<1,0<cos A<1,
tanA>0,cotA>0(2)tan A?cot A=1锐角三角函数的意义
小结:锐角三角函数函数描述了直角三角形中边与角的关系,它又是一个变量之间重要的函数关系,即新奇,又富有魅力,你可要与它建立好感情噢! 结束寄语
Rt△AB1C1∽Rt△_______∽Rt△_________......
所以 =__________=__________. 观察想一想
一般情况下,在Rt△ABC中,当锐角A取固定值时,∠A的对边与邻边的比值是一个固定值的吗?
∠A的对边与斜边的比值是一个固定值的吗?
∠A的邻边与斜边的比值是一个固定值的吗?
思 考在Rt△ABC中,对于锐角A的每一个确定的值,其对边与邻边的比值是惟一确定的.
概括 我们同样可以发现,对于锐角A的每一个确定的值,其对边与斜边、邻边与斜边、邻边与对边的比值也是惟一确定的. 因此这几个比值都是锐角∠A的函数,
记作sin A、cos A、tan A、cot A 正弦:sin A= ,
余弦:cos A= ,
正切:tan A= ,
余切:cot A= .
锐角三角函数的定义
锐角三角函数的定义在Rt△ABC中,∠C=90°,
sinA= ,cosA= ,
tanA= ,cotA= 。 显然,锐角三角函数值都是正实数,并且
0<sin A<1,0<cos A<1,tanA>0,cotA>0根据三角函数的定义,我们还有:tan A?cot A=1锐角三角函数的定义注意2.sinA,cosA,tanA,cotA都是整体符号,不能看成sin·A,cos · A,tan · A,cot · A1.当角A固定时,它的三角函数值都是固定的,与角A的边长短无关3.若用三个大写字母表示一个角时,在表示它的三角函数时,角的符号“∠”不能省略.例: 1.如图,在Rt△MNP中,∠N=90゜.
∠P的对边是________,∠P的邻边是______;
∠M的对边是_______,∠M的邻边是______; 试一试2.求出如图所示的Rt△DEC(∠E=90゜)中∠D的四个三角函数值. 试一试1.在Rt△ABC中,∠C=90°,sinA= , 求∠B的四个三角函数值。分析 在直角三角形中,给出锐角的任何一个三角函数值都等于给出两条边长的比,若其中一条边长已知,就可求出另一条边长;若两边都未给出,则可考虑设辅助未知数。解 在Rt△ABC中,由sinA=
可设BC=4k,AB=5k,k≠0则
有AC=
∴sinB= ,cosB=
tanB= ,cotB=例 题2.如图,在Rt△ABC中,∠ACB=90°, BC=5,AC=4, (1)求sinA ,sinB的值, (2)过点C作CD⊥AB,求cos∠ACD.例 题3.在等腰△ABC中,AB=AC=13,BC=10,
求tanB,cotC.例 题求锐角三角函数时,勾股定理的运用是很重要的.基础练习1.在△ABC中,∠C=90°,BC=3,tanB=
则AB= 。
2.在△ABC中,∠C=90°,如果tanA= ,那么sinB=( )。
A B C D
3.在△ABC中,已知AC=3,BC=4,AB=5,那么下列结论成立的是( )。
A sinA= B cosA=
C tanA= D cotA=4.如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定5.已知∠A,∠B为锐角
(1)若∠A=∠B,则tanA tanB;
(2)若tanA=tanB,则∠A ∠B.基础练习 6.sinA=2m-3(A为锐角),则m的取值范围是___.在Rt△ABC中,∠C=90°,
sinA= ,cosA= ,
tanA= ,cotA= 。 (1)0<sin A<1,0<cos A<1,
tanA>0,cotA>0(2)tan A?cot A=1锐角三角函数的意义
小结:锐角三角函数函数描述了直角三角形中边与角的关系,它又是一个变量之间重要的函数关系,即新奇,又富有魅力,你可要与它建立好感情噢! 结束寄语
