安徽省合肥市庐江县七校联盟2022—2023学年下学期第一次月考七年级数学试卷(含解析)
文档属性
| 名称 | 安徽省合肥市庐江县七校联盟2022—2023学年下学期第一次月考七年级数学试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 226.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-06 00:00:00 | ||
图片预览




文档简介
2023年庐江县七年级数学七校联盟第一次月考试卷
(试卷满分150分,考试时间120分钟)
一、单选题(共10题;共40分)
1.(4分)下列各数中,是无理数的是( )
A. B. C. D.
2.(4分)如图,若m∥n,∠1=105 o,则∠2=( )
A.55 o B.60 o C.65 o D.75 o
3.(4分)下列实数中是无理数的是( )
A.-1 B. C. D.0
4.(4分)下列实数中,是无理数的为( )
A.0 B. C.﹣ D.
5.(4分)平面内有两两不重合的直线和,已知,则的位置关系是( )
A.互相平行 B.可能平行,可能不平行
C.互相垂直 D.可能垂直,可能不垂直
6.(4分)已知三角形的三个顶点坐标分别是A(﹣2,﹣1),B(1,﹣2),C(0,2).若将△ABC先向右平移2个单位,再向上平移3个单位长度,则所得三角形的三个顶点的坐标分别为( )
A.(﹣4,2),(﹣1,1),(﹣2,5)
B.(0,2),(3,1),(2,5)
C.(﹣4,5),(﹣1,4),(﹣2,8)
D.(1,1),(4,0),(3,4)
7.(4分)下列计算,结果正确的是( )
A. ≈0.066 B. ≈30
C. ≈60.4 D. ≈96
8.(4分)5的平方根为( )
A.25 B. C. D.
9.(4分)如图,以数轴的单位长度线段为边作一个 正方形,以表示数2的点为圆心,正方形对角线长为半径画弧,交数轴于点A,则点A表示的数是( )
A. B.2 C.1 D.1+
10.(4分)如图所示,由△ABC平移得到的三角形的个数是( )
A.5 B.15 C.8 D.6
二、填空题(共4题;共20分)
11.(5分)如图,为了把河中的水引到 处,可过点 作 于 ,然后沿 开渠,这样做可使所开的渠道最短,这种设计的依据是 .
12.(5分)在实数 , , , 中,最小的数是 .
13.(5分)设 的整数部分和小数部分分别是 、 ,则 , 。
14.(5分)如图,已知AB∥CD,F为CD上一点,∠EFD=60°,∠AEC=2∠CEF,若6°<∠BAE<15°,∠C的度数为整数,则∠C的度数为 .
三、计算题(共2题;共16分)
15.(8分)计算.
(1)(4分)| |﹣
(2)(4分) ( +3)﹣2 .
16.(8分)已知m+2的算术平方根是4,2m+n+1的立方根是3,求m﹣n的平方根.
四、解答题(共2题;共16分)
17.(8分)已知,如图, 于点 , , 分别交 于点 ,试判断 与 的位置关系,并说明理由.
18.(8分)如图,在四边形ABCD中,∠A=∠C,BE平分∠ABC,DF平分∠ADC,试说明BE∥DF.
五、综合题(共5题;共58分)
19.(10分)综合题。
(1)(5分)已知a,b是有理数且满足:a是﹣27的立方根, =7,求a2+2b的值;
(2)(5分)已知a﹣b=2,a﹣c= ,求(b﹣c)2+3(b﹣c)+ 的值.
20.(10分)如图,已知EF//BC,∠B=∠1.
(1)(5分)AB与CD有怎样的位置关系?请说明理由;
(2)(5分)若∠BAD+∠2= ,那么∠G与∠3有怎样的数量关系?为什么?
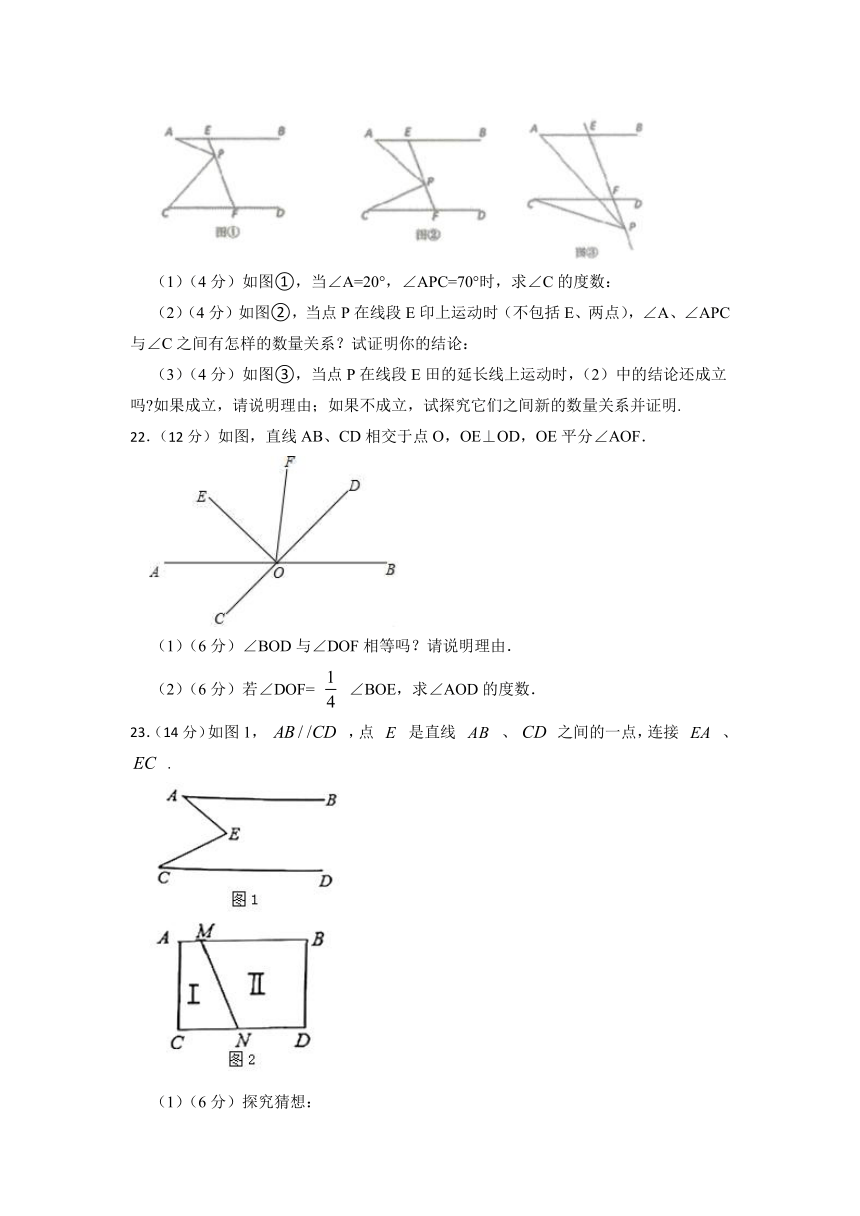
21.(12分)已知AB∥CD,线段E田分别与AB、CD相交于点E、F.
(1)(4分)如图①,当∠A=20°,∠APC=70°时,求∠C的度数:
(2)(4分)如图②,当点P在线段E印上运动时(不包括E、两点),∠A、∠APC与∠C之间有怎样的数量关系?试证明你的结论:
(3)(4分)如图③,当点P在线段E田的延长线上运动时,(2)中的结论还成立吗 如果成立,请说明理由;如果不成立,试探究它们之间新的数量关系并证明.
22.(12分)如图,直线AB、CD相交于点O,OE⊥OD,OE平分∠AOF.
(1)(6分)∠BOD与∠DOF相等吗?请说明理由.
(2)(6分)若∠DOF= ∠BOE,求∠AOD的度数.
23.(14分)如图1, ,点 是直线 、 之间的一点,连接 、 .
(1)(6分)探究猜想:
①若 ,则 ▲ .
②若 ,则 ▲ .
③猜想图1中 、 、 的关系,并证明你的结论.
(2)(8分)拓展应用:
如图2, ,线段 把 这个封闭区域分为I、II两部分(不含边界),点 是位于这两个区域内的任意一点,请直接写出 、 、 的关系.
答案解析部分
1.【答案】B
【解析】【解答】解:A. 是有理数,故该选项不符合题意;
B. 是无理数,故该选项符合题意;
C. 是有理数,故该选项不符合题意;
D. 是有理数,故该选项不符合题意;
故答案为:B
【分析】根据无理数的定义逐项判断即可。
2.【答案】D
【解析】【解答】解:∵m∥n,∴∠1+∠2=180°,又∠1=105°,∴∠2=75°.
故答案为:D.
【分析】两直线平行,同旁内角互补,得到∠1+∠2=180°.
3.【答案】C
【解析】【解答】解:A.-1是整数,属于有理数,故本选项不合题意;
B.是分数,属于有理数,故本选项不合题意;
C.是无理数,故本选项符合题意;
D.0是整数,属于有理数,故本选项不符合题意.
故答案为:C.
【分析】无理数常见三种形式如下:①开方开不尽的数;②与π有关的式子;③无限不循环小数,据此判断即可.
4.【答案】B
【解析】【解答】解:0,﹣ , 是有理数,
是无理数,
故B符合题意.
故答案为:B.
【分析】根据无理数的定义判断.无理数是无限不循环小数,有限小数和无限循环小数是有理数.
5.【答案】A
【解析】【分析】根据两条直线分别于第三条直线垂直,这两条直线不是重叠就是互相平行,可选A。
【点评】本题难度较低,主要考查学生对平行线性质知识点的掌握,运用性质定理判断即可。
6.【答案】B
【解析】【解答】根据横坐标,右移加,左移减;纵坐标,上移加,下移减可得:
∵A(﹣2,﹣1),B(1,﹣2),C(0,2),
∴将△ABC先向右平移2个单位,再向上平移3个单位长度,所得坐标是:(﹣2+2,﹣1+3),(1+2,﹣2+3),(0+2,2+3),
即:(0,2,)(3,1)(2,5),
故答案为:B
【分析】根据横坐标,右移加,左移减;纵坐标,上移加,下移减,进而可得出答案。
7.【答案】B
【解析】【解答】A. ≈0.656,故本选项不符合题意;
B. ≈30,故本选项符合题意;
C. ≈50.4,故本选项不符合题意;
D. ≈9.65,故本选项不符合题意.
故答案为:B.
【分析】利用计算器对各项分别进行计算,再利用排除法求解。
8.【答案】D
【解析】【解答】解:5的平方根是
故答案为:D
【分析】根据平方根的性质,正数有两个平方根,它们互为相反数
9.【答案】B
【解析】【解答】解: 根据勾股定理可得,正方形的对角线为
设点A表示的数为x
∴2-x=
∴x=2-
故答案为:B.
【分析】根据题意,数轴上两点之间的距离为较大的数减去较小的数,即可得到答案。
10.【答案】A
【解析】【解答】△ABC经过平移后得到的三角形有一个顶角向下,图中这样的三角形有5个,即得A.
【分析】把握平移是沿直线方向的移动,图形的形状在某方向上不变,这是区分平移和旋转的重要方法.
11.【答案】垂线段最短
【解析】【解答】过C点引CD⊥AB于D,然后沿CD开渠,可使所开渠道最短,根据垂线段最短.
故答案为垂线段最短
【分析】根据垂线段最短进行分析即可.
12.【答案】-3
【解析】【解答】解:∵ ,
∴ (两个负数比较大小,绝对值大的数反而小)
又∵ 、 均为正数,比 大(正数都大于零,零大于一切负数)
因此最小的数是-3
故答案为-3.
【分析】先分析这几个实数中的符号(正数都比负数大),再比较负数的大小,取负数的绝对值进行比较,从而得到答案.
13.【答案】4;
【解析】【解答】因为4<6<9,所以2< <3,
即 的整数部分是2,
所以2+ 的整数部分是4,小数部分是2+ 4= 2,
即x=4,y= 2
故填:(1). 4 (2). .
【分析】先找到 介于哪两个整数之间,从而找到整数部分,小数部分让原数减去整数部分,然后代入求值即可.
14.【答案】36°或37°
【解析】【解答】解:如图,过E作EG∥AB,
∵AB∥CD,
∴GE∥CD,
∴∠BAE=∠AEG,∠DFE=∠GEF,
∴∠AEF=∠BAE+∠DFE,
设∠CEF=x,则∠AEC=2x,
∴x+2x=∠BAE+60°,
∴∠BAE=3x﹣60°,
又∵6°<∠BAE<15°,
∴6°<3x﹣60°<15°,
解得22°<x<25°,
又∵∠DFE是△CEF的外角,∠C的度数为整数,
∴∠C=60°﹣23°=37°或∠C=60°﹣24°=36°,
故答案为:36°或37°.
【分析】先过E作EG∥AB,根据平行线的性质可得∠AEF=∠BAE+∠DFE,再设∠CEF=x,则∠AEC=2x,根据6°<∠BAE<15°,即可得到6°<3x﹣60°<15°,解得22°<x<25°,进而得到∠C的度数.
15.【答案】(1)解:| |﹣
=2﹣9
=﹣7
(2)解: ( +3)﹣2
=3+3 ﹣2
=3+
【解析】【【分析】(1)首先计算开方,然后计算减法,求出算式的值是多少即可.(2)应用乘法分配律,求出算式的值是多少即可.
16.【答案】解:由题意得, ,
解得: ,
∴m﹣n=16,m﹣n的平方根是±4
【解析】【分析】根据算术平方根的意义可得m+2=,根据立方根的意义可得2m+n+1=,联立解方程组即可求得m、n的值,则m﹣n的平方根可求解。
17.【答案】解:
证明:∵ ,∴
∴ ,∵ ,∴
∴
∴ ,∴
∴ ,∴
【解析】【分析】由已知条件结合平行线的判定定理可得DG∥AB,则∠1=∠DAB,结合∠1=∠2可得∠2=∠DAB,推出EF∥AD,由平行线的性质可得∠BFE=∠BDA,最后根据AD⊥BC进行解答.
18.【答案】解:∵∠A+∠ABC+∠C+∠CDA=360°
而∠A=∠C,BE平分∠ABC,DF平分∠CDA
∴2∠A+2∠ABE+2∠ADF=360°
即∠A+∠ABE+∠ADF=180°
又∠A+∠ABE+∠AEB=180°
∴∠AEB=∠ADF
∴BE∥DF.
【解析】【分析】根据四边形内角和是360°和角平分线的定义,可求得∠A+∠ABE+∠ADF=180°;再利用三角形的内角和是180°,求得∠A+∠ABE+∠AEB=180°,由此可得出∠AEB=∠ADF,根据同位角相等,两直线平行即可证得BE∥DF.
19.【答案】(1)解:∵a是﹣27的立方根,
∴a=﹣3,
∵ =7,
∴b=±7,
∴a2+2b=23或﹣5
(2)解:∵a﹣b=2,a﹣c= ,
∴b﹣c=﹣ ,
∴b﹣c+ =0,
∴原式=(b﹣c+ )2=0
【解析】【分析】(1)根据立方根的意义,算术平方根的性质即可解决问题.(2)首先求出b﹣c的值,利用完全平方公式即可解决问题.
20.【答案】(1)AB∥CD,理由如下:
∵EF//BC,
∴∠2=∠1,
∵∠B=∠1,
∴∠B=∠2,
∴AB∥CD;
(2)∠G=∠3,理由如下:
∵∠B=∠2,∠BAD+∠2= ,
∴∠BAD+∠B= ,
∴AD∥BC,
∴∠G=∠3.
【解析】【分析】(1)根据平行线的性质,由EF∥BC可得∠2=∠1,于是可证∠B=∠2,根据平行线的判定定理可得 AB∥CD ;
(2)根据∠B=∠2,可得∠BAD+∠B= ,于是可证AD∥BC,则根据平行线的性质可得∠G=∠3.
21.【答案】(1)解:∠C=50°
(2)解:∠A+∠C=∠APC
(3)解:∠A-∠C=∠APC
【解析】【分析】(1)过点P作PO∥AB,推出AB∥PO∥CD
,根据平行线的性质得出∠APO=∠A=20°,∠C=∠CPO,代入求出即可;
(2)过点P作PO∥AB,推出AB∥PO∥CD,根据平行线性质得出∠APO=∠A,∠C=∠CPO,根据角的运算,求出即可;
(3)过点P作PO∥AB,推出AB∥PO∥CD,根据平行线性质得出∠APO=∠A,∠C=∠CPO,根据角的运算分析计算即可。
22.【答案】(1)解:∠BOD=∠DOF,
∵OE⊥OD,
∴∠DOE=90°,
∴∠EOF+∠DOF=90°,∠AOE+∠BOD=90°,
∵OE平分∠AOF,
∴∠AOE=∠EOF,
∴∠BOD=∠DOF
(2)解:∵∠DOF= ∠BOE,
∴设∠DOF=x°,则∠BOE=4x°,∠BOD=x°,
∴∠DOE=∠BOE﹣∠BOD=3x°,
∵∠DOE=90°,
∴3x=90,即x=30,
∴∠BOD=30°,
∴∠AOD=180°﹣∠BOD=150°.
【解析】【分析】(1)由OE⊥OD知∠EOF+∠DOF=90°,∠AOE+∠BOD=90°,根据∠AOE=∠EOF即可得∠BOD=∠DOF;(2)由∠DOF= ∠BOE可∠DOF=x°,则∠BOE=4x°,∠BOD=x°,从而得∠DOE=∠BOE﹣∠BOD=3x°,根据∠DOE=90°可得x的值,继而根据∠AOD=180°﹣∠BOD即可得出答案.
23.【答案】(1)70°;65°;
解:过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠AEF=∠EAB,∠CEF=∠ECD,
∴∠AEC=∠AEF+∠CEF= + ;
(2)解:如果点E在I区域内 + + =360°,如果点E在II区域内, = + ;
【解析】【解答】(1)解:如图所示,①过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∵∠EAB=20°,∠ECD=50°,
∴∠AEF=∠EAB=20°,∠CEF=∠ECD=50°,
∴∠AEC=∠AEF+∠CEF=70°;
②过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∵∠EAB=25°,∠ECD=40°,
∴∠AEF=∠EAB=25°,∠CEF=∠ECD=40°,
∴∠AEC=∠AEF+∠CEF=65°;
【分析】(1)①过点E作EF∥AB,再由平行线的性质“两直线平行,内错角相等;两直线平行同旁内角互补;两直线平行同位角相等”即可得出结论;②③根据①的过程可得出结论;(2)根据题意画出图形,再根据平行线的性质及三角形内角和定理即可得出结论.
(试卷满分150分,考试时间120分钟)
一、单选题(共10题;共40分)
1.(4分)下列各数中,是无理数的是( )
A. B. C. D.
2.(4分)如图,若m∥n,∠1=105 o,则∠2=( )
A.55 o B.60 o C.65 o D.75 o
3.(4分)下列实数中是无理数的是( )
A.-1 B. C. D.0
4.(4分)下列实数中,是无理数的为( )
A.0 B. C.﹣ D.
5.(4分)平面内有两两不重合的直线和,已知,则的位置关系是( )
A.互相平行 B.可能平行,可能不平行
C.互相垂直 D.可能垂直,可能不垂直
6.(4分)已知三角形的三个顶点坐标分别是A(﹣2,﹣1),B(1,﹣2),C(0,2).若将△ABC先向右平移2个单位,再向上平移3个单位长度,则所得三角形的三个顶点的坐标分别为( )
A.(﹣4,2),(﹣1,1),(﹣2,5)
B.(0,2),(3,1),(2,5)
C.(﹣4,5),(﹣1,4),(﹣2,8)
D.(1,1),(4,0),(3,4)
7.(4分)下列计算,结果正确的是( )
A. ≈0.066 B. ≈30
C. ≈60.4 D. ≈96
8.(4分)5的平方根为( )
A.25 B. C. D.
9.(4分)如图,以数轴的单位长度线段为边作一个 正方形,以表示数2的点为圆心,正方形对角线长为半径画弧,交数轴于点A,则点A表示的数是( )
A. B.2 C.1 D.1+
10.(4分)如图所示,由△ABC平移得到的三角形的个数是( )
A.5 B.15 C.8 D.6
二、填空题(共4题;共20分)
11.(5分)如图,为了把河中的水引到 处,可过点 作 于 ,然后沿 开渠,这样做可使所开的渠道最短,这种设计的依据是 .
12.(5分)在实数 , , , 中,最小的数是 .
13.(5分)设 的整数部分和小数部分分别是 、 ,则 , 。
14.(5分)如图,已知AB∥CD,F为CD上一点,∠EFD=60°,∠AEC=2∠CEF,若6°<∠BAE<15°,∠C的度数为整数,则∠C的度数为 .
三、计算题(共2题;共16分)
15.(8分)计算.
(1)(4分)| |﹣
(2)(4分) ( +3)﹣2 .
16.(8分)已知m+2的算术平方根是4,2m+n+1的立方根是3,求m﹣n的平方根.
四、解答题(共2题;共16分)
17.(8分)已知,如图, 于点 , , 分别交 于点 ,试判断 与 的位置关系,并说明理由.
18.(8分)如图,在四边形ABCD中,∠A=∠C,BE平分∠ABC,DF平分∠ADC,试说明BE∥DF.
五、综合题(共5题;共58分)
19.(10分)综合题。
(1)(5分)已知a,b是有理数且满足:a是﹣27的立方根, =7,求a2+2b的值;
(2)(5分)已知a﹣b=2,a﹣c= ,求(b﹣c)2+3(b﹣c)+ 的值.
20.(10分)如图,已知EF//BC,∠B=∠1.
(1)(5分)AB与CD有怎样的位置关系?请说明理由;
(2)(5分)若∠BAD+∠2= ,那么∠G与∠3有怎样的数量关系?为什么?
21.(12分)已知AB∥CD,线段E田分别与AB、CD相交于点E、F.
(1)(4分)如图①,当∠A=20°,∠APC=70°时,求∠C的度数:
(2)(4分)如图②,当点P在线段E印上运动时(不包括E、两点),∠A、∠APC与∠C之间有怎样的数量关系?试证明你的结论:
(3)(4分)如图③,当点P在线段E田的延长线上运动时,(2)中的结论还成立吗 如果成立,请说明理由;如果不成立,试探究它们之间新的数量关系并证明.
22.(12分)如图,直线AB、CD相交于点O,OE⊥OD,OE平分∠AOF.
(1)(6分)∠BOD与∠DOF相等吗?请说明理由.
(2)(6分)若∠DOF= ∠BOE,求∠AOD的度数.
23.(14分)如图1, ,点 是直线 、 之间的一点,连接 、 .
(1)(6分)探究猜想:
①若 ,则 ▲ .
②若 ,则 ▲ .
③猜想图1中 、 、 的关系,并证明你的结论.
(2)(8分)拓展应用:
如图2, ,线段 把 这个封闭区域分为I、II两部分(不含边界),点 是位于这两个区域内的任意一点,请直接写出 、 、 的关系.
答案解析部分
1.【答案】B
【解析】【解答】解:A. 是有理数,故该选项不符合题意;
B. 是无理数,故该选项符合题意;
C. 是有理数,故该选项不符合题意;
D. 是有理数,故该选项不符合题意;
故答案为:B
【分析】根据无理数的定义逐项判断即可。
2.【答案】D
【解析】【解答】解:∵m∥n,∴∠1+∠2=180°,又∠1=105°,∴∠2=75°.
故答案为:D.
【分析】两直线平行,同旁内角互补,得到∠1+∠2=180°.
3.【答案】C
【解析】【解答】解:A.-1是整数,属于有理数,故本选项不合题意;
B.是分数,属于有理数,故本选项不合题意;
C.是无理数,故本选项符合题意;
D.0是整数,属于有理数,故本选项不符合题意.
故答案为:C.
【分析】无理数常见三种形式如下:①开方开不尽的数;②与π有关的式子;③无限不循环小数,据此判断即可.
4.【答案】B
【解析】【解答】解:0,﹣ , 是有理数,
是无理数,
故B符合题意.
故答案为:B.
【分析】根据无理数的定义判断.无理数是无限不循环小数,有限小数和无限循环小数是有理数.
5.【答案】A
【解析】【分析】根据两条直线分别于第三条直线垂直,这两条直线不是重叠就是互相平行,可选A。
【点评】本题难度较低,主要考查学生对平行线性质知识点的掌握,运用性质定理判断即可。
6.【答案】B
【解析】【解答】根据横坐标,右移加,左移减;纵坐标,上移加,下移减可得:
∵A(﹣2,﹣1),B(1,﹣2),C(0,2),
∴将△ABC先向右平移2个单位,再向上平移3个单位长度,所得坐标是:(﹣2+2,﹣1+3),(1+2,﹣2+3),(0+2,2+3),
即:(0,2,)(3,1)(2,5),
故答案为:B
【分析】根据横坐标,右移加,左移减;纵坐标,上移加,下移减,进而可得出答案。
7.【答案】B
【解析】【解答】A. ≈0.656,故本选项不符合题意;
B. ≈30,故本选项符合题意;
C. ≈50.4,故本选项不符合题意;
D. ≈9.65,故本选项不符合题意.
故答案为:B.
【分析】利用计算器对各项分别进行计算,再利用排除法求解。
8.【答案】D
【解析】【解答】解:5的平方根是
故答案为:D
【分析】根据平方根的性质,正数有两个平方根,它们互为相反数
9.【答案】B
【解析】【解答】解: 根据勾股定理可得,正方形的对角线为
设点A表示的数为x
∴2-x=
∴x=2-
故答案为:B.
【分析】根据题意,数轴上两点之间的距离为较大的数减去较小的数,即可得到答案。
10.【答案】A
【解析】【解答】△ABC经过平移后得到的三角形有一个顶角向下,图中这样的三角形有5个,即得A.
【分析】把握平移是沿直线方向的移动,图形的形状在某方向上不变,这是区分平移和旋转的重要方法.
11.【答案】垂线段最短
【解析】【解答】过C点引CD⊥AB于D,然后沿CD开渠,可使所开渠道最短,根据垂线段最短.
故答案为垂线段最短
【分析】根据垂线段最短进行分析即可.
12.【答案】-3
【解析】【解答】解:∵ ,
∴ (两个负数比较大小,绝对值大的数反而小)
又∵ 、 均为正数,比 大(正数都大于零,零大于一切负数)
因此最小的数是-3
故答案为-3.
【分析】先分析这几个实数中的符号(正数都比负数大),再比较负数的大小,取负数的绝对值进行比较,从而得到答案.
13.【答案】4;
【解析】【解答】因为4<6<9,所以2< <3,
即 的整数部分是2,
所以2+ 的整数部分是4,小数部分是2+ 4= 2,
即x=4,y= 2
故填:(1). 4 (2). .
【分析】先找到 介于哪两个整数之间,从而找到整数部分,小数部分让原数减去整数部分,然后代入求值即可.
14.【答案】36°或37°
【解析】【解答】解:如图,过E作EG∥AB,
∵AB∥CD,
∴GE∥CD,
∴∠BAE=∠AEG,∠DFE=∠GEF,
∴∠AEF=∠BAE+∠DFE,
设∠CEF=x,则∠AEC=2x,
∴x+2x=∠BAE+60°,
∴∠BAE=3x﹣60°,
又∵6°<∠BAE<15°,
∴6°<3x﹣60°<15°,
解得22°<x<25°,
又∵∠DFE是△CEF的外角,∠C的度数为整数,
∴∠C=60°﹣23°=37°或∠C=60°﹣24°=36°,
故答案为:36°或37°.
【分析】先过E作EG∥AB,根据平行线的性质可得∠AEF=∠BAE+∠DFE,再设∠CEF=x,则∠AEC=2x,根据6°<∠BAE<15°,即可得到6°<3x﹣60°<15°,解得22°<x<25°,进而得到∠C的度数.
15.【答案】(1)解:| |﹣
=2﹣9
=﹣7
(2)解: ( +3)﹣2
=3+3 ﹣2
=3+
【解析】【【分析】(1)首先计算开方,然后计算减法,求出算式的值是多少即可.(2)应用乘法分配律,求出算式的值是多少即可.
16.【答案】解:由题意得, ,
解得: ,
∴m﹣n=16,m﹣n的平方根是±4
【解析】【分析】根据算术平方根的意义可得m+2=,根据立方根的意义可得2m+n+1=,联立解方程组即可求得m、n的值,则m﹣n的平方根可求解。
17.【答案】解:
证明:∵ ,∴
∴ ,∵ ,∴
∴
∴ ,∴
∴ ,∴
【解析】【分析】由已知条件结合平行线的判定定理可得DG∥AB,则∠1=∠DAB,结合∠1=∠2可得∠2=∠DAB,推出EF∥AD,由平行线的性质可得∠BFE=∠BDA,最后根据AD⊥BC进行解答.
18.【答案】解:∵∠A+∠ABC+∠C+∠CDA=360°
而∠A=∠C,BE平分∠ABC,DF平分∠CDA
∴2∠A+2∠ABE+2∠ADF=360°
即∠A+∠ABE+∠ADF=180°
又∠A+∠ABE+∠AEB=180°
∴∠AEB=∠ADF
∴BE∥DF.
【解析】【分析】根据四边形内角和是360°和角平分线的定义,可求得∠A+∠ABE+∠ADF=180°;再利用三角形的内角和是180°,求得∠A+∠ABE+∠AEB=180°,由此可得出∠AEB=∠ADF,根据同位角相等,两直线平行即可证得BE∥DF.
19.【答案】(1)解:∵a是﹣27的立方根,
∴a=﹣3,
∵ =7,
∴b=±7,
∴a2+2b=23或﹣5
(2)解:∵a﹣b=2,a﹣c= ,
∴b﹣c=﹣ ,
∴b﹣c+ =0,
∴原式=(b﹣c+ )2=0
【解析】【分析】(1)根据立方根的意义,算术平方根的性质即可解决问题.(2)首先求出b﹣c的值,利用完全平方公式即可解决问题.
20.【答案】(1)AB∥CD,理由如下:
∵EF//BC,
∴∠2=∠1,
∵∠B=∠1,
∴∠B=∠2,
∴AB∥CD;
(2)∠G=∠3,理由如下:
∵∠B=∠2,∠BAD+∠2= ,
∴∠BAD+∠B= ,
∴AD∥BC,
∴∠G=∠3.
【解析】【分析】(1)根据平行线的性质,由EF∥BC可得∠2=∠1,于是可证∠B=∠2,根据平行线的判定定理可得 AB∥CD ;
(2)根据∠B=∠2,可得∠BAD+∠B= ,于是可证AD∥BC,则根据平行线的性质可得∠G=∠3.
21.【答案】(1)解:∠C=50°
(2)解:∠A+∠C=∠APC
(3)解:∠A-∠C=∠APC
【解析】【分析】(1)过点P作PO∥AB,推出AB∥PO∥CD
,根据平行线的性质得出∠APO=∠A=20°,∠C=∠CPO,代入求出即可;
(2)过点P作PO∥AB,推出AB∥PO∥CD,根据平行线性质得出∠APO=∠A,∠C=∠CPO,根据角的运算,求出即可;
(3)过点P作PO∥AB,推出AB∥PO∥CD,根据平行线性质得出∠APO=∠A,∠C=∠CPO,根据角的运算分析计算即可。
22.【答案】(1)解:∠BOD=∠DOF,
∵OE⊥OD,
∴∠DOE=90°,
∴∠EOF+∠DOF=90°,∠AOE+∠BOD=90°,
∵OE平分∠AOF,
∴∠AOE=∠EOF,
∴∠BOD=∠DOF
(2)解:∵∠DOF= ∠BOE,
∴设∠DOF=x°,则∠BOE=4x°,∠BOD=x°,
∴∠DOE=∠BOE﹣∠BOD=3x°,
∵∠DOE=90°,
∴3x=90,即x=30,
∴∠BOD=30°,
∴∠AOD=180°﹣∠BOD=150°.
【解析】【分析】(1)由OE⊥OD知∠EOF+∠DOF=90°,∠AOE+∠BOD=90°,根据∠AOE=∠EOF即可得∠BOD=∠DOF;(2)由∠DOF= ∠BOE可∠DOF=x°,则∠BOE=4x°,∠BOD=x°,从而得∠DOE=∠BOE﹣∠BOD=3x°,根据∠DOE=90°可得x的值,继而根据∠AOD=180°﹣∠BOD即可得出答案.
23.【答案】(1)70°;65°;
解:过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠AEF=∠EAB,∠CEF=∠ECD,
∴∠AEC=∠AEF+∠CEF= + ;
(2)解:如果点E在I区域内 + + =360°,如果点E在II区域内, = + ;
【解析】【解答】(1)解:如图所示,①过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∵∠EAB=20°,∠ECD=50°,
∴∠AEF=∠EAB=20°,∠CEF=∠ECD=50°,
∴∠AEC=∠AEF+∠CEF=70°;
②过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∵∠EAB=25°,∠ECD=40°,
∴∠AEF=∠EAB=25°,∠CEF=∠ECD=40°,
∴∠AEC=∠AEF+∠CEF=65°;
【分析】(1)①过点E作EF∥AB,再由平行线的性质“两直线平行,内错角相等;两直线平行同旁内角互补;两直线平行同位角相等”即可得出结论;②③根据①的过程可得出结论;(2)根据题意画出图形,再根据平行线的性质及三角形内角和定理即可得出结论.
同课章节目录
