26.2 二次函数的图象与性质4[下学期]
文档属性
| 名称 | 26.2 二次函数的图象与性质4[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 56.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-05-03 13:11:00 | ||
图片预览


文档简介
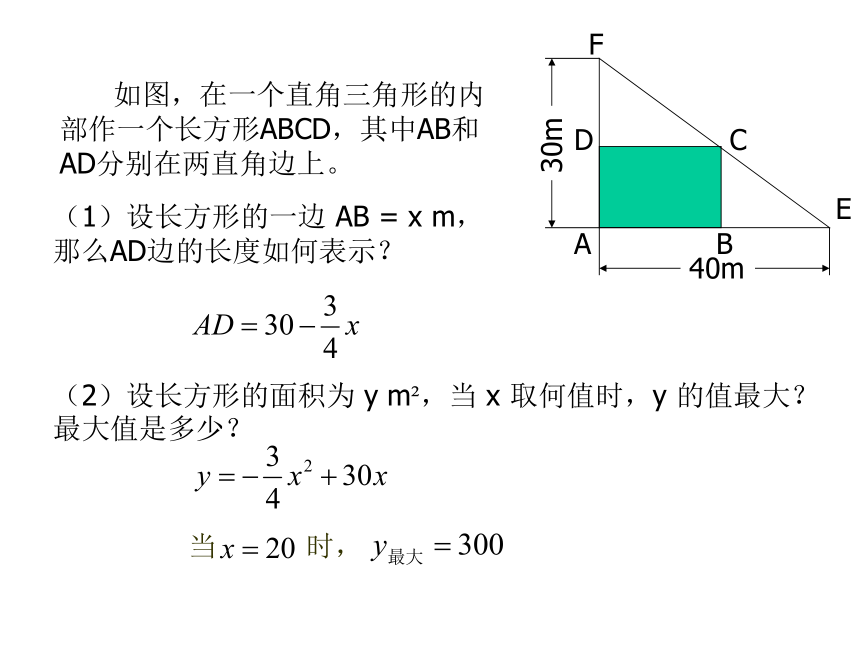
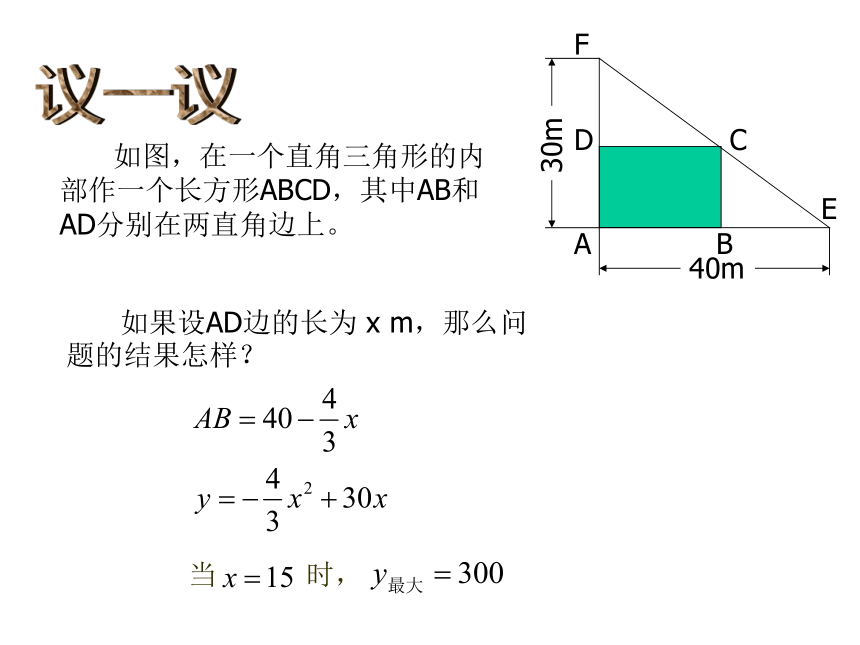
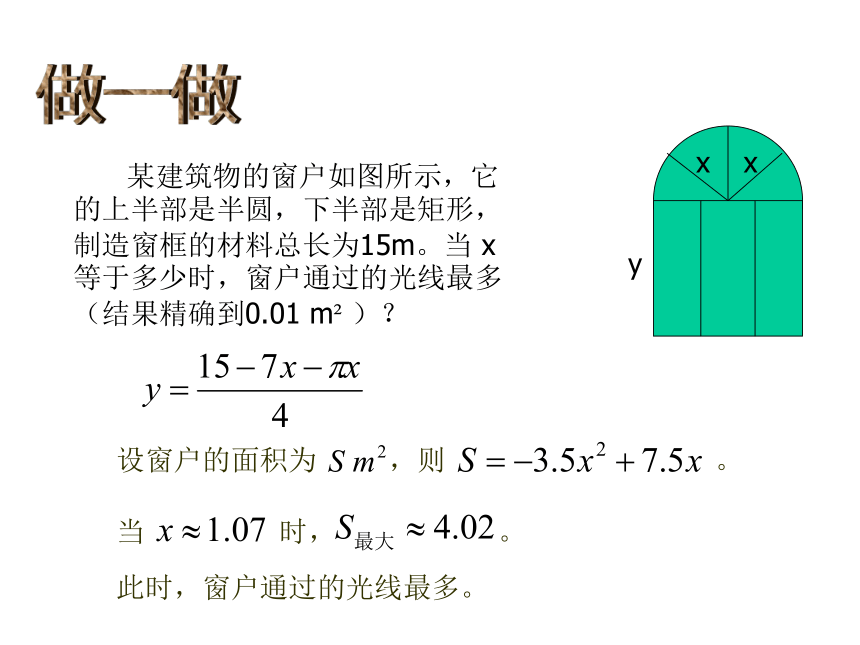
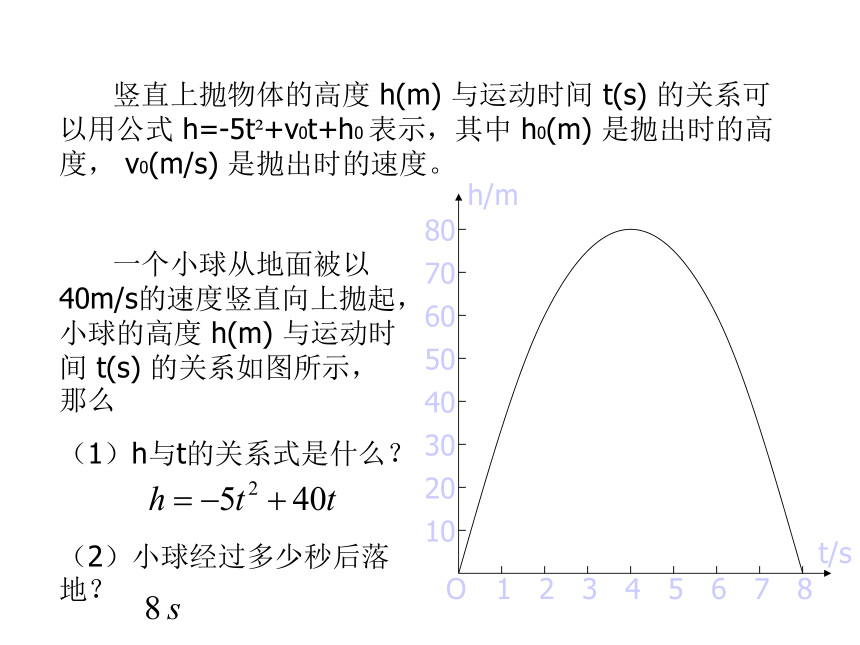
课件14张PPT。二次函数的图象与性质4 如图,在一个直角三角形的内部作一个长方形ABCD,其中AB和AD分别在两直角边上。ABDC40m30m(1)设长方形的一边 AB = x m,那么AD边的长度如何表示?(2)设长方形的面积为 y m2,当 x 取何值时,y 的值最大?最大值是多少?议一议 如图,在一个直角三角形的内部作一个长方形ABCD,其中AB和AD分别在两直角边上。ABDC40m30m 如果设AD边的长为 x m,那么问题的结果怎样?FE做一做 某建筑物的窗户如图所示,它的上半部是半圆,下半部是矩形,制造窗框的材料总长为15m。当 x等于多少时,窗户通过的光线最多(结果精确到0.01 m2 )?xxy此时,窗户通过的光线最多。议一议 回顾《何时获得最大利润》和《最大面积是多少》这两节解决问题的过程,试总结解决此类问题的基本思路。(1)理解问题;(2)分析问题中的变量和常量,以及它们之间的关系;(3)用数学的方式表示它们之间的关系;(4)数学求解;(5)检验结果的合理性、拓展等。 竖直上抛物体的高度 h(m) 与运动时间 t(s) 的关系可以用公式 h=-5t2+v0t+h0 表示,其中 h0(m) 是抛出时的高度, v0(m/s) 是抛出时的速度。 一个小球从地面被以40m/s的速度竖直向上抛起,小球的高度 h(m) 与运动时间 t(s) 的关系如图所示,那么
(1)h与t的关系式是什么?
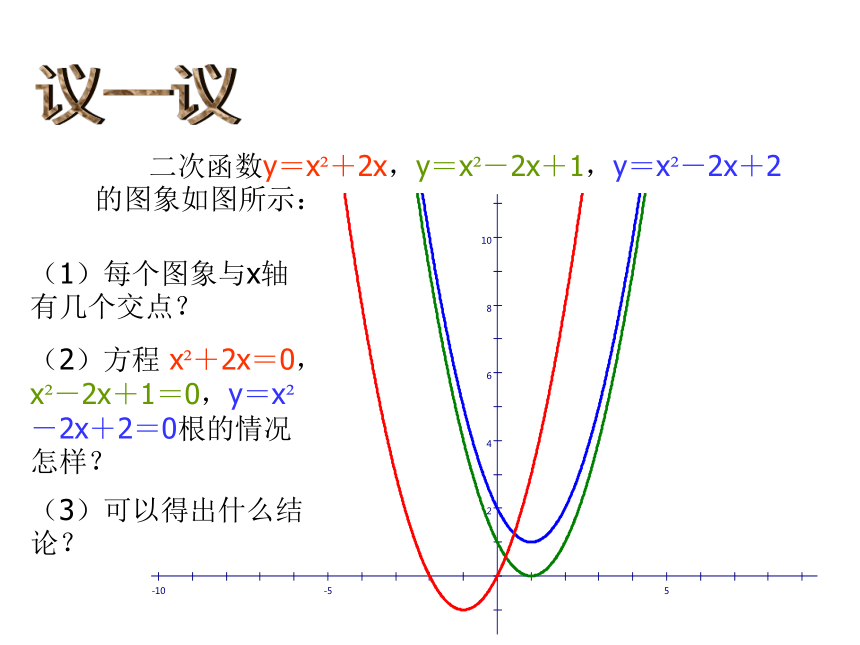
(2)小球经过多少秒后落地?O123456781020304050607080h/mt/s议一议 二次函数y=x2+2x,y=x2-2x+1,y=x2-2x+2的图象如图所示:(1)每个图象与x轴有几个交点?(2)方程 x2+2x=0,x2-2x+1=0,y=x2-2x+2=0根的情况怎样?(3)可以得出什么结论?一元二次方程二次函数二次函数的图象没有实根图象与x轴没有交点 竖直上抛物体的高度 h(m) 与运动时间 t(s) 的关系可以用公式 h=-5t2+v0t+h0 表示,其中 h0(m) 是抛出时的高度, v0(m/s) 是抛出时的速度。 一个小球从地面被以40m/s的速度竖直向上抛起,小球的高度 h(m) 与运动时间 t(s) 的关系如图所示,那么
(1)h与t的关系式是什么?
(2)小球经过多少秒后落地?O123456781020304050607080h/mt/s议一议 二次函数y=x2+2x,y=x2-2x+1,y=x2-2x+2的图象如图所示:(1)每个图象与x轴有几个交点?(2)方程 x2+2x=0,x2-2x+1=0,y=x2-2x+2=0根的情况怎样?(3)可以得出什么结论?一元二次方程二次函数二次函数的图象没有实根图象与x轴没有交点O123456781020304050607080h/mt/s想一想 在前面的小球上抛问题中,何时小球离地面的高度是60m?方法一:利用图象(3)
方程 -4.9t2+19.6t=0 的根的实际意义
——足球离开地面及落地的时间
方程 -4.9t2+19.6t=14.7 的根的实际意义
——足球离地面高度是14.7m时的时间利用二次函数的图象估计一元二次方程 的根。 由图象可知方程有两个根,一个在-5和-4之间,另一个在2和3之间。
(1)h与t的关系式是什么?
(2)小球经过多少秒后落地?O123456781020304050607080h/mt/s议一议 二次函数y=x2+2x,y=x2-2x+1,y=x2-2x+2的图象如图所示:(1)每个图象与x轴有几个交点?(2)方程 x2+2x=0,x2-2x+1=0,y=x2-2x+2=0根的情况怎样?(3)可以得出什么结论?一元二次方程二次函数二次函数的图象没有实根图象与x轴没有交点 竖直上抛物体的高度 h(m) 与运动时间 t(s) 的关系可以用公式 h=-5t2+v0t+h0 表示,其中 h0(m) 是抛出时的高度, v0(m/s) 是抛出时的速度。 一个小球从地面被以40m/s的速度竖直向上抛起,小球的高度 h(m) 与运动时间 t(s) 的关系如图所示,那么
(1)h与t的关系式是什么?
(2)小球经过多少秒后落地?O123456781020304050607080h/mt/s议一议 二次函数y=x2+2x,y=x2-2x+1,y=x2-2x+2的图象如图所示:(1)每个图象与x轴有几个交点?(2)方程 x2+2x=0,x2-2x+1=0,y=x2-2x+2=0根的情况怎样?(3)可以得出什么结论?一元二次方程二次函数二次函数的图象没有实根图象与x轴没有交点O123456781020304050607080h/mt/s想一想 在前面的小球上抛问题中,何时小球离地面的高度是60m?方法一:利用图象(3)
方程 -4.9t2+19.6t=0 的根的实际意义
——足球离开地面及落地的时间
方程 -4.9t2+19.6t=14.7 的根的实际意义
——足球离地面高度是14.7m时的时间利用二次函数的图象估计一元二次方程 的根。 由图象可知方程有两个根,一个在-5和-4之间,另一个在2和3之间。
