分类复习牛吃草问题(课件)-六年级下册数学苏教版(共27张PPT)
文档属性
| 名称 | 分类复习牛吃草问题(课件)-六年级下册数学苏教版(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 182.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-05 15:22:22 | ||
图片预览








文档简介
(共27张PPT)
牛吃草问题
牛吃草问题最先在牛顿的《普通算术》中出现,所以人们又习惯上称之为牛顿的牛吃草问题。
2、牛顿牧场
牛顿牧场是理想牧场,在这个牧场上草是匀速生长的
1、牛吃草问题
3、牛吃草问题三部曲
(1)先算新生草量
(2)再算原有草量
(3)最后计算问题
例1 牧场上有一片牧草,可供27头牛吃6周,或者供23头牛吃9周.如果牧草每周匀速生长,可供21头牛吃几周?
分析]
这个问题的难点在于草的总量在变,但牧场上的牧草时刻都在匀速生长,因此,草的总量是由两部分组成:
(1)某个时间期限前,草场上原有的草量,并且是不变的
(2)某个时间期限后,草场每单位时间生长而新增的草量,并
且也是不变的。
因此,必须先设法求出这两个量来 ,我们可以画以下线段图:
解:假设1头牛每周吃的草的数量是1份
27×6=162份……原草量+6周的生长量
23×9=207份……原草量+9周的生长量
草每周的生长量:
(207-162)÷(9-6)=15份
原草量:
27×6-15×6=72份
23×9-15×6=72份
15头 吃
剩下21-15=6头
72份
15份
+
6头牛吃72份草能吃几周?
72÷(21-15)=12周
同一片牧场中的“牛吃草”问题,一般的解法可总结为:
⑴设定1头牛1天吃草量为“1”;
⑵草的生长速度=(对应牛的头数×对应较多天数-相应牛的头数×对应吃 的少的天数)÷(吃的较多的天数-吃的较少的天数);
⑶原来的草量=(对应牛的头数×吃的天数)-(草的生长速度×吃的天数)
⑷吃的天数=原来的草量÷(牛的头数-草的生长速度);
⑸牛的头数=原来的草量÷吃的天数+草的生长速度.
“牛吃草”问题有很多的变例,像抽水问题、检票口检票问题等等,
只有理解了“牛吃草”问题的本质和解题思路,
才能以不变应万变,轻松解决此类问题
[自主训练] 牧场上长满了青草,而且每天还在匀速生长,这片牧场上的草可供9头牛吃20天,可供15头牛吃10天,如果要供18头牛吃,可吃几天?
解:假设1头牛1天吃的草的数量是1份
9×20=180份……原草量+20天的生长量
15×10=150份……原草量+10天的生长量
草每天的生长量:
(180-150)÷(20-10)=3份
原草量:
180-20×3=120份
150-10×3=120份
3头 吃
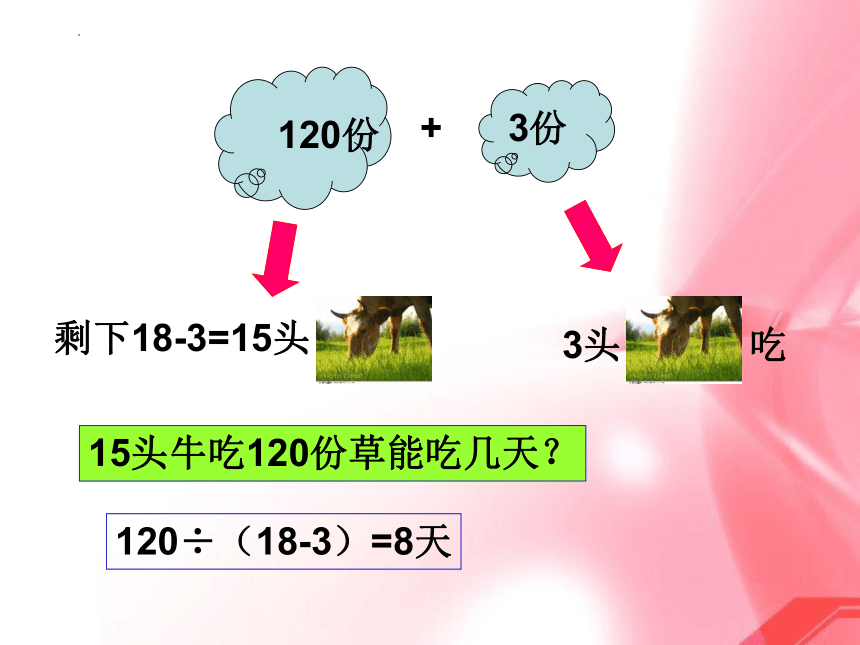
剩下18-3=15头
120份
3份
+
15头牛吃120份草能吃几天?
120÷(18-3)=8天
例2 由于天气逐渐冷起来,牧场上的草不仅不长大,反而以固定速度在减少。已知某块草地上的草可供20头牛吃5天,或可供15头牛吃6天。照此计算,可供多少头牛吃10天?
解:假设1头牛1天吃的草的数量是1份
20×5=100份……原草量-5天的减少量
15×6=90份……原草量-6天的减少量
草每天的减少量:
(100-90)÷(6-5)=10份
原草量:
100+5×10=150份
或90+6×10=150份
剩下150-100=50份
150份
10份
-
50份草可供多少头牛吃10天?
(150-10×10)÷10=5头
10天减少
10×10=100份
[自主训练] 由于天气逐渐寒冷,牧场上的牧草每天以均匀的速度减少,经测算,牧场上的草可供30头牛吃8天,可供25头牛吃9天,那么可供21头牛吃几天?
解:假设1头牛1天吃的草的数量是1份
30×8=240份……原草量-8天的减少量
25×9=225份……原草量-9天的减少量
草每天的减少量:
(240-225)÷(9-8)=15份
原草量:
240+8×15=360份
或220+9×15=360份
例3 一只船有一个漏洞,水以均匀的速度进入船内,发现漏洞时已经进入了一些水,如果用12人舀水,3小时舀完,如果只有5个人舀水,要10小时才能舀完,现在想在6小时舀完,需要多少人?
解:假设1人1小时舀1份水
12×3=36份……原水量+3小时进水量
5×10=50份……原水量+10小时的进水量
每小时的进水量:
(50-36)÷(10-3)=2份
原水量:
36-3×2=30份
或50-10×2=30份
30份
2份
+
(30+12)份水需要几个人6小时舀完?
(30+12)÷6=7小时
2×6=12份
360份
15份
-
360份草可供21头牛吃几天?
360÷(21+15)=10天
15头牛在吃
[自主训练] 有一口水井,持续不断地涌出水,而且每分钟涌出的水量相等。如果用3台抽水机抽水36分钟可以抽完,如果用5台抽水机抽水,20分钟可以抽完,现在用8台抽水机抽完水,需要几分钟?
解:假设1台抽水机1小时抽1份水
3×36=108份……原水量+36分钟进水量
5×20=100份……原水量+20分钟的进水量
每分钟的进水量:
(108-100)÷(36-20)=0.5份
原水量:
108-36×0.5=90份
或100-20×0.5=90份
90份
0.5份
+
90份水需要8台抽水机几分钟舀完?
90÷(8-0.5)=12小时
8-0.5=7.5份
例4 自动扶梯以均匀速度由下往上行驶着,两位性急的孩子要从扶梯上楼。已知男孩每分钟走20级梯级,女孩每分钟走15级梯级,结果男孩用了5分钟到达楼上,女孩用了6分钟到达楼上。问:该扶梯共有多少级?
20×5 =
自动扶梯的级数-5分钟减少的级数
15×6 =
自动扶梯的级数-6分钟减少的级数
男孩:
女孩:
每分钟减少的级数=
(20×5-15×6) ÷(6-5)=10(级)
自动扶梯的级数=
20×5+5×10=150(级)
[自主训练] 两个顽皮孩子逆着自动扶梯行驶的方向行走,男孩每秒可走3级阶梯,女孩每秒可走2级阶梯,结果从扶梯的一端到达另一端男孩走了100秒,女孩走了300秒。问该扶梯共有多少级?
3×100=自动扶梯级数+100秒新增的级数
2×300=自动扶梯级数+300秒新增的级数
自动扶梯级数=
(2×300-3×100)÷(300-100)=1.5(级)
每秒新增的级数:
3×100-100×1.5=150(级)
例5 某车站在检票前若干分钟就开始排队,每分钟来的旅客人数一样多。从开始检票到等候检票的队伍消失,同时开4个检票口需30分钟,同时开5个检票口需20分钟。如果同时打开7个检票口,那么需要多少分钟?
假设每分钟每个检票口进的人数为1份
4×30=
原有等待的人数+30分钟新增的人数
5×20=
原有等待的人数+20分钟新增的人数
每分钟新增的人数=
(4×30-5×20)÷(30-20)
= 2(份)
原有等待的人数=
4×30-30×2=60(份)
专门安排2个检票口检新增加的人
60÷(7-2)=12(分钟)
[自主训练] 盛德美9时开门营业,开门前就有人等候入场,如果第一个顾客来时起,每分钟来的顾客人数同样多,那么开4个门等候的人全部进入商场要8分钟,开6个门等候的人全部进入商场只要4分钟,问第一个顾客到达时是几时几分?
假设每分钟每个检票口进的人数为1份
4×8=
原有等待的人数+8分钟新增的人数
6×4=
原有等待的人数+6分钟新增的人数
每分钟新增的人数=
(4×8-6×4)÷(8-6)
= 4(份)
原有等待的人数=
4×8-8×4=0(份)
例6 有3个牧场长满草,第一牧场33公亩,可供22头牛吃54天,第二牧场28公亩,可供17头牛吃84天,第三牧场40公亩,可供多少头牛吃24天?
解:假设1头牛1天吃1份草
22×54=1188份
平均每公顷有草量:
1188÷33=36份
第二块草量为:
17×84=1428份
平均每公顷有草量:
1428÷28=51份
第一块草量为:
每公顷草每天的生长量为:
(51-36)÷(84-54)=0.5份
每公亩的草量:
36-54×0.5=9份
或51-84×0.5=9份
(40×9+40×0.5×24)÷24=35(头)
第三块牧场可供:
[自主训练] 有3个牧场长满草,第一牧场10公亩,可供20头牛吃50天,第二牧场15公亩,可供40头牛吃30天,第三牧场40公亩,可供多少头牛吃24天?(每块地每公亩的草量相同而且都是匀速生长)
假设每头牛每天的吃草量是1份
20×50=10公亩原有草量+10公亩50天新增量
40×30=15公亩原有草量+15公亩30天新增量
20×50÷10=100
40×30÷15=80
=1公亩原有草量+1公亩50天新增量
=1公亩原有草量+1公亩30天新增量
1公亩每天生长量=
(100-80)÷(50-30)=1(份)
1公亩的草量=
100-1×50=50(份)
(40×50+40×1×24)÷24
例7 有一牧场长满牧草,每天牧草匀速生长,这个牧场可供17头牛吃30天,可供19头牛吃24天,现在有若干头牛在吃草,6天后,4头牛死亡,余下的牛吃2天将草吃完,问原来有多少头牛?
解:假设1头牛1天吃1份草
草每天的生长量为:
(17×30-19×24)÷(30-24)=9份
原有的草量为:
17×30-30×9=240份
或29×24-24×9=240份
若4头牛不死,这群牛在6+2=8天内共吃草
240+9×8+2×4=320份
320份草可共几头牛吃8天?
320÷8=40头
[自主训练] 一个牧场上长满了青草,这些牧草可供5只羊吃30天,或者可供7只羊吃20天,现在牧场上有8只羊,10天后,有2只羊死亡,剩下的羊多少天可以将牧场上的草吃完?
解:假设1只羊1天吃1份草
草每天的生长量为:
(5×30-7×20)÷(30-20)=1份
原有的草量为:
5×30-30×1=120份
或7×20-20×1=120份
10天后所剩草量:
120+10×1-8×10=50份
10天还有6只羊可吃几天?
50÷(6-1)=10天
牛吃草问题
牛吃草问题最先在牛顿的《普通算术》中出现,所以人们又习惯上称之为牛顿的牛吃草问题。
2、牛顿牧场
牛顿牧场是理想牧场,在这个牧场上草是匀速生长的
1、牛吃草问题
3、牛吃草问题三部曲
(1)先算新生草量
(2)再算原有草量
(3)最后计算问题
例1 牧场上有一片牧草,可供27头牛吃6周,或者供23头牛吃9周.如果牧草每周匀速生长,可供21头牛吃几周?
分析]
这个问题的难点在于草的总量在变,但牧场上的牧草时刻都在匀速生长,因此,草的总量是由两部分组成:
(1)某个时间期限前,草场上原有的草量,并且是不变的
(2)某个时间期限后,草场每单位时间生长而新增的草量,并
且也是不变的。
因此,必须先设法求出这两个量来 ,我们可以画以下线段图:
解:假设1头牛每周吃的草的数量是1份
27×6=162份……原草量+6周的生长量
23×9=207份……原草量+9周的生长量
草每周的生长量:
(207-162)÷(9-6)=15份
原草量:
27×6-15×6=72份
23×9-15×6=72份
15头 吃
剩下21-15=6头
72份
15份
+
6头牛吃72份草能吃几周?
72÷(21-15)=12周
同一片牧场中的“牛吃草”问题,一般的解法可总结为:
⑴设定1头牛1天吃草量为“1”;
⑵草的生长速度=(对应牛的头数×对应较多天数-相应牛的头数×对应吃 的少的天数)÷(吃的较多的天数-吃的较少的天数);
⑶原来的草量=(对应牛的头数×吃的天数)-(草的生长速度×吃的天数)
⑷吃的天数=原来的草量÷(牛的头数-草的生长速度);
⑸牛的头数=原来的草量÷吃的天数+草的生长速度.
“牛吃草”问题有很多的变例,像抽水问题、检票口检票问题等等,
只有理解了“牛吃草”问题的本质和解题思路,
才能以不变应万变,轻松解决此类问题
[自主训练] 牧场上长满了青草,而且每天还在匀速生长,这片牧场上的草可供9头牛吃20天,可供15头牛吃10天,如果要供18头牛吃,可吃几天?
解:假设1头牛1天吃的草的数量是1份
9×20=180份……原草量+20天的生长量
15×10=150份……原草量+10天的生长量
草每天的生长量:
(180-150)÷(20-10)=3份
原草量:
180-20×3=120份
150-10×3=120份
3头 吃
剩下18-3=15头
120份
3份
+
15头牛吃120份草能吃几天?
120÷(18-3)=8天
例2 由于天气逐渐冷起来,牧场上的草不仅不长大,反而以固定速度在减少。已知某块草地上的草可供20头牛吃5天,或可供15头牛吃6天。照此计算,可供多少头牛吃10天?
解:假设1头牛1天吃的草的数量是1份
20×5=100份……原草量-5天的减少量
15×6=90份……原草量-6天的减少量
草每天的减少量:
(100-90)÷(6-5)=10份
原草量:
100+5×10=150份
或90+6×10=150份
剩下150-100=50份
150份
10份
-
50份草可供多少头牛吃10天?
(150-10×10)÷10=5头
10天减少
10×10=100份
[自主训练] 由于天气逐渐寒冷,牧场上的牧草每天以均匀的速度减少,经测算,牧场上的草可供30头牛吃8天,可供25头牛吃9天,那么可供21头牛吃几天?
解:假设1头牛1天吃的草的数量是1份
30×8=240份……原草量-8天的减少量
25×9=225份……原草量-9天的减少量
草每天的减少量:
(240-225)÷(9-8)=15份
原草量:
240+8×15=360份
或220+9×15=360份
例3 一只船有一个漏洞,水以均匀的速度进入船内,发现漏洞时已经进入了一些水,如果用12人舀水,3小时舀完,如果只有5个人舀水,要10小时才能舀完,现在想在6小时舀完,需要多少人?
解:假设1人1小时舀1份水
12×3=36份……原水量+3小时进水量
5×10=50份……原水量+10小时的进水量
每小时的进水量:
(50-36)÷(10-3)=2份
原水量:
36-3×2=30份
或50-10×2=30份
30份
2份
+
(30+12)份水需要几个人6小时舀完?
(30+12)÷6=7小时
2×6=12份
360份
15份
-
360份草可供21头牛吃几天?
360÷(21+15)=10天
15头牛在吃
[自主训练] 有一口水井,持续不断地涌出水,而且每分钟涌出的水量相等。如果用3台抽水机抽水36分钟可以抽完,如果用5台抽水机抽水,20分钟可以抽完,现在用8台抽水机抽完水,需要几分钟?
解:假设1台抽水机1小时抽1份水
3×36=108份……原水量+36分钟进水量
5×20=100份……原水量+20分钟的进水量
每分钟的进水量:
(108-100)÷(36-20)=0.5份
原水量:
108-36×0.5=90份
或100-20×0.5=90份
90份
0.5份
+
90份水需要8台抽水机几分钟舀完?
90÷(8-0.5)=12小时
8-0.5=7.5份
例4 自动扶梯以均匀速度由下往上行驶着,两位性急的孩子要从扶梯上楼。已知男孩每分钟走20级梯级,女孩每分钟走15级梯级,结果男孩用了5分钟到达楼上,女孩用了6分钟到达楼上。问:该扶梯共有多少级?
20×5 =
自动扶梯的级数-5分钟减少的级数
15×6 =
自动扶梯的级数-6分钟减少的级数
男孩:
女孩:
每分钟减少的级数=
(20×5-15×6) ÷(6-5)=10(级)
自动扶梯的级数=
20×5+5×10=150(级)
[自主训练] 两个顽皮孩子逆着自动扶梯行驶的方向行走,男孩每秒可走3级阶梯,女孩每秒可走2级阶梯,结果从扶梯的一端到达另一端男孩走了100秒,女孩走了300秒。问该扶梯共有多少级?
3×100=自动扶梯级数+100秒新增的级数
2×300=自动扶梯级数+300秒新增的级数
自动扶梯级数=
(2×300-3×100)÷(300-100)=1.5(级)
每秒新增的级数:
3×100-100×1.5=150(级)
例5 某车站在检票前若干分钟就开始排队,每分钟来的旅客人数一样多。从开始检票到等候检票的队伍消失,同时开4个检票口需30分钟,同时开5个检票口需20分钟。如果同时打开7个检票口,那么需要多少分钟?
假设每分钟每个检票口进的人数为1份
4×30=
原有等待的人数+30分钟新增的人数
5×20=
原有等待的人数+20分钟新增的人数
每分钟新增的人数=
(4×30-5×20)÷(30-20)
= 2(份)
原有等待的人数=
4×30-30×2=60(份)
专门安排2个检票口检新增加的人
60÷(7-2)=12(分钟)
[自主训练] 盛德美9时开门营业,开门前就有人等候入场,如果第一个顾客来时起,每分钟来的顾客人数同样多,那么开4个门等候的人全部进入商场要8分钟,开6个门等候的人全部进入商场只要4分钟,问第一个顾客到达时是几时几分?
假设每分钟每个检票口进的人数为1份
4×8=
原有等待的人数+8分钟新增的人数
6×4=
原有等待的人数+6分钟新增的人数
每分钟新增的人数=
(4×8-6×4)÷(8-6)
= 4(份)
原有等待的人数=
4×8-8×4=0(份)
例6 有3个牧场长满草,第一牧场33公亩,可供22头牛吃54天,第二牧场28公亩,可供17头牛吃84天,第三牧场40公亩,可供多少头牛吃24天?
解:假设1头牛1天吃1份草
22×54=1188份
平均每公顷有草量:
1188÷33=36份
第二块草量为:
17×84=1428份
平均每公顷有草量:
1428÷28=51份
第一块草量为:
每公顷草每天的生长量为:
(51-36)÷(84-54)=0.5份
每公亩的草量:
36-54×0.5=9份
或51-84×0.5=9份
(40×9+40×0.5×24)÷24=35(头)
第三块牧场可供:
[自主训练] 有3个牧场长满草,第一牧场10公亩,可供20头牛吃50天,第二牧场15公亩,可供40头牛吃30天,第三牧场40公亩,可供多少头牛吃24天?(每块地每公亩的草量相同而且都是匀速生长)
假设每头牛每天的吃草量是1份
20×50=10公亩原有草量+10公亩50天新增量
40×30=15公亩原有草量+15公亩30天新增量
20×50÷10=100
40×30÷15=80
=1公亩原有草量+1公亩50天新增量
=1公亩原有草量+1公亩30天新增量
1公亩每天生长量=
(100-80)÷(50-30)=1(份)
1公亩的草量=
100-1×50=50(份)
(40×50+40×1×24)÷24
例7 有一牧场长满牧草,每天牧草匀速生长,这个牧场可供17头牛吃30天,可供19头牛吃24天,现在有若干头牛在吃草,6天后,4头牛死亡,余下的牛吃2天将草吃完,问原来有多少头牛?
解:假设1头牛1天吃1份草
草每天的生长量为:
(17×30-19×24)÷(30-24)=9份
原有的草量为:
17×30-30×9=240份
或29×24-24×9=240份
若4头牛不死,这群牛在6+2=8天内共吃草
240+9×8+2×4=320份
320份草可共几头牛吃8天?
320÷8=40头
[自主训练] 一个牧场上长满了青草,这些牧草可供5只羊吃30天,或者可供7只羊吃20天,现在牧场上有8只羊,10天后,有2只羊死亡,剩下的羊多少天可以将牧场上的草吃完?
解:假设1只羊1天吃1份草
草每天的生长量为:
(5×30-7×20)÷(30-20)=1份
原有的草量为:
5×30-30×1=120份
或7×20-20×1=120份
10天后所剩草量:
120+10×1-8×10=50份
10天还有6只羊可吃几天?
50÷(6-1)=10天
