二次函数及其图像[下学期]

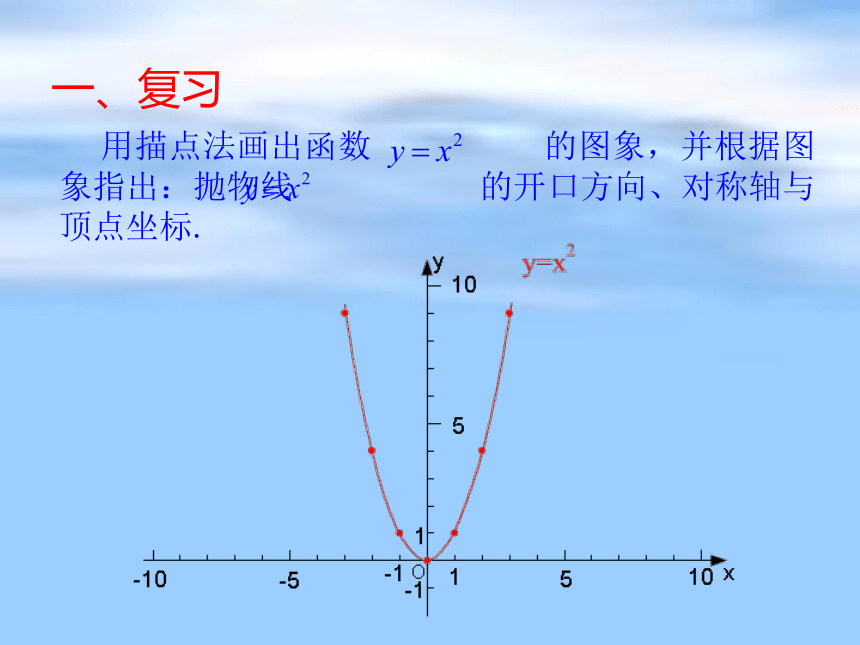
课件27张PPT。函数及其图象 二次函数 的图象 一、复习 用描点法画出函数 的图象，并根据图象指出：抛物线 的开口方向、对称轴与顶点坐标.
二 新课例1 在同一平面直角坐标系画出函数 、 与 的图象. 演示问题1：观察函数对应值表，你能想象出三个图象之间的关系吗？(与学生分析函数对应值表)观察图象回答下列问题的图象是什么？图片问题2：抛物线 ， 与 的开
口方向，对称轴，顶点坐标有何异同？ 问题3：抛物线 ， 与 有什么
关系？ 问题4：抛物线 是由抛物线 沿y轴怎样
移动得到的？抛物线 呢？
问题5：你认为是什么决定了会这样平移？
图片图片图片练习一 总结1(2) 抛物线 的性质：
时，开口向上， 时，开口向下；
②对称轴为 　轴；
③顶点坐标（０, ） ．
例2 在同一平面直角坐标系内画出 ，
与 的图象． 演示问题1：观察函数对应值表，你能想象出三个函数图
象之间的关系吗？(与学生分析函数值表)观察图象回答下列问题图片图片问题3：抛物线 ， 与 有
什么关系？问题4：抛物线 由抛物线 沿 轴
怎样移动得到的？抛物线 呢？问题5：你认为是什么决定了会这样平移？图片图片练习二总结2(2)抛物线 的性质：
① 时,开口向上； 时，开口向下；
抛物线 的图象可由 的图象左右平
移得到, ,向右平移, ,向左平移,平移 个单位.②对称轴是直线 ；
③顶点坐标是 .例3 在同一直角坐标系内，画出函数 ,
与 的图象. 演示问题1:观察函数对应值表,你能想象出三个函数图象之
间的关系吗?问题2：观察图象，请说出抛物线 ，
与 的开口方向、对称轴与顶点
坐标？图片图片问题4：由例1、例2、例3，你能说出
抛物线 是由
抛物线　　　　怎样移动得到的？问题3: 你能总结出抛物线 有什么特点
吗? 练习三本节小结二次函数 的图象是什么, 图象是
怎么来的.②图象可由二次函数 的图象平移得到.① 二次函数 的图象是抛物线. （2）抛物线 的性质.① 时，开口向上； 时，开口向下； ② 对称轴是直线 ； ③ 顶点坐标是 . 练习1、已知函数 的图像如图所示，则函数
　　　　　　的图像可能是( ).
B
2、函数y＝x2＋bx＋c与y＝bx＋c在同一坐标系中的图
象大致是（ ）.
3、已知二次函数y＝ax2＋bx＋c的图象如下图所示，
则下列6个代数式ab、ac、a＋b＋c、a－b＋c、2a＋b、
2a－b中，其值为正的式子的个数为（ ）.
CA Ａ.2个 ; Ｂ.3个;
Ｃ.4个 ;Ｄ.4个以上.
6、已知二次函数的顶点是（2，－1），且与y轴的交
点到原点的距离是2，则这个二次函数的解析式是
____________________________.


BB 或 7、已知：一次函数 的图象和二次函数
的图象交于点 和 .
①求一次函数解析式；
②若二次函数开口向上，与y轴交于点C，且
的面积为12，求二次函数的解析式.
① ② .答案:思考题：想一想抛物线 的图象是
什么？如何去求它的对称轴及顶点坐标？抛物线在生活中的应用完返回返回返回返回返回返回返回中央电教馆资源中心制作2003.11