二次函数的图象及性质[下学期]

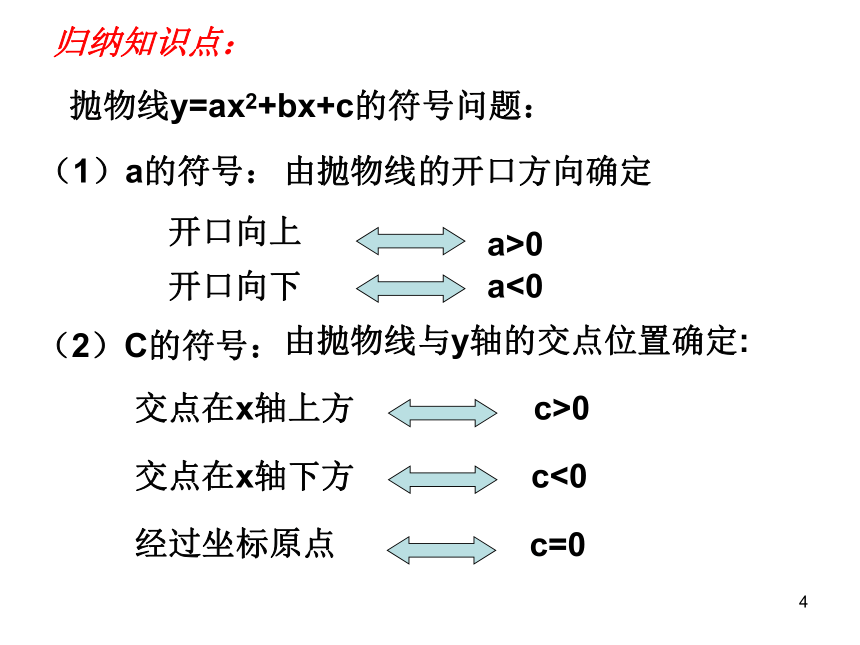
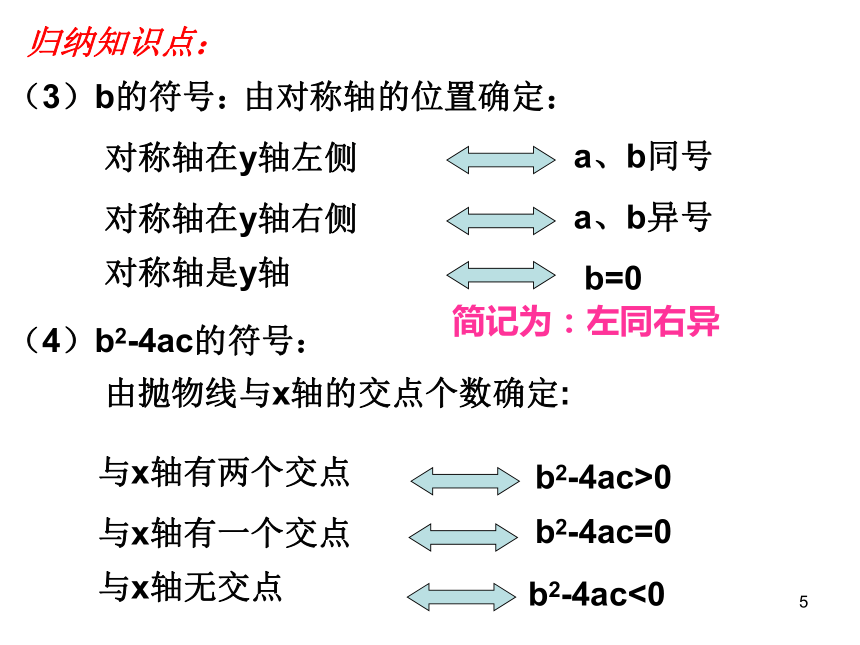
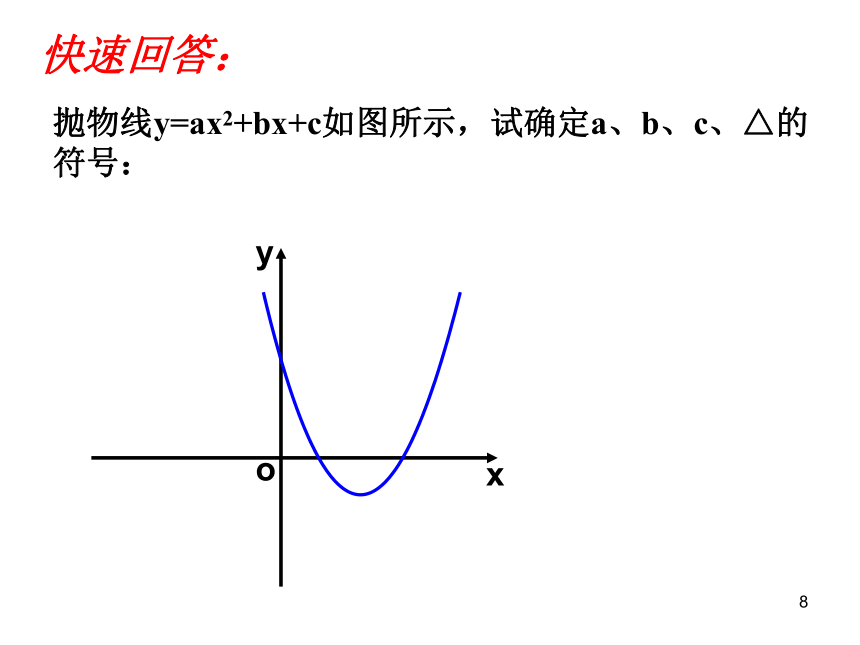
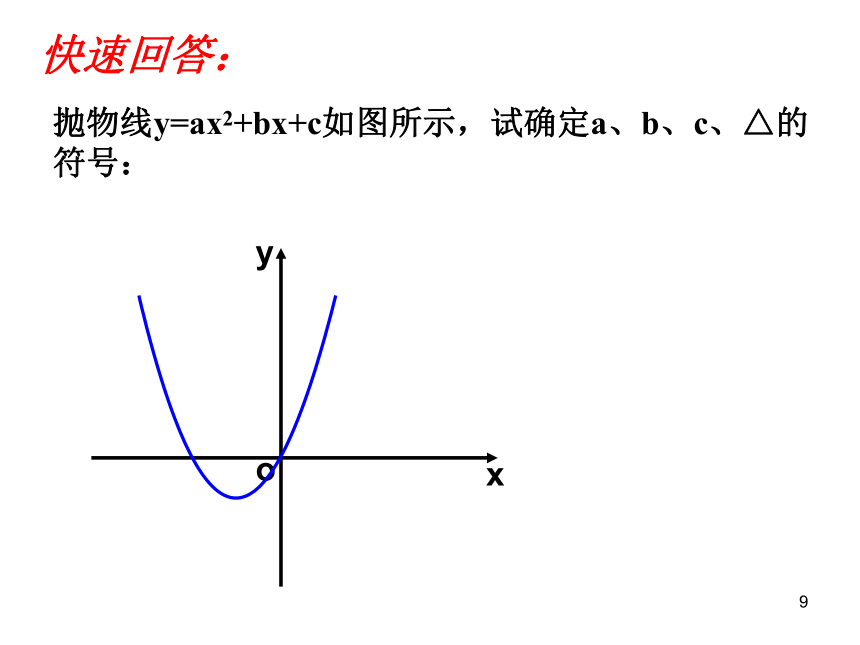
课件21张PPT。1二次函数中的符号问题新密市兴华公学1二次函数中的符号问题（a、b、c、△等符号）1回味知识点：1、抛物线y=ax2+bx+c的开口方向与什么有关？2、抛物线y=ax2+bx+c与y轴的交点是 .3、抛物线y=ax2+bx+c的对称轴是 .1归纳知识点：抛物线y=ax2+bx+c的符号问题：（1）a的符号：由抛物线的开口方向确定开口向上a>0开口向下a<0（2）C的符号：由抛物线与y轴的交点位置确定:交点在x轴上方c>0交点在x轴下方c<0经过坐标原点c=01（3）b的符号：由对称轴的位置确定：对称轴在y轴左侧a、b同号对称轴在y轴右侧a、b异号对称轴是y轴b=0（4）b2-4ac的符号：由抛物线与x轴的交点个数确定:与x轴有两个交点b2-4ac>0与x轴有一个交点b2-4ac=0与x轴无交点b2-4ac<0归纳知识点：简记为：左同右异1归纳知识点：抛物线y=ax2+bx+c的符号问题：（5）a+b+c的符号：由x=1时抛物线上的点的位置确定（6）a-b+c的符号：由x=-1时抛物线上的点的位置确定你还可想到啥？1利用以上知识主要解决以下几方面问题：（1）由a,b,c,?的符号确定抛物线在坐标系中的大 致位置；（2）由抛物线的位置确定系数a,b,c,?等符号及有关a,b,c的代数式的符号；1快速回答：抛物线y=ax2+bx+c如图所示，试确定a、b、c、△的符号：xoy1抛物线y=ax2+bx+c如图所示，试确定a、b、c、△的符号：xyo快速回答：1抛物线y=ax2+bx+c如图所示，试确定a、b、c、△的符号：xyo快速回答：1抛物线y=ax2+bx+c如图所示，试确定a、b、c、△的符号：xyo快速回答：1抛物线y=ax2+bx+c如图所示，试确定a、b、c、△的符号：xyo快速回答：1练一练：1.已知：二次函数y=ax2+bx+c的图象如图所示，则点M（ ，a）在（ ）A、第一象限
B、第二象限
C、第三象限
D、第四象限 xoyD1练一练：2、已知：二次函数y=ax2+bx+c的图象如图所示，下列结论中：①b＞0；②c<0；③4a+2b+c ＞ 0；④（a+c)2＜b2，其中正确的个数是 （ ）
A、4个 B、3个
C、2个 D、1个B1练一练：3、已知：二次函数y=ax2+bx+c的图象如图所示，下列结论中：①abc＞0；②b=2a；③a+b+c＜0；④a+b-c＞0; ⑤a-b+c＞0正确的个数是 （ ）
A、2个 B、3个
C、4个 D、5个C14.二次函数y=ax2+bx+c的图象的一部分如图，已知它的顶点M在第二象限，且经过A(1,0),B(0,1),请判断实数a的范围,并说明理由.想一想：1 5.(06.芜湖市)如图，在平面直角坐标系中，二次函数y=ax2+c（a<0）的图象过正方形ABOC的三个顶点A、B、C，则ac的值是 .再想一想：-216.（06.浙江省）如图，二次函数y=ax2+bx+c的图象开口向上，图象经过点（-1，2）和（1，0），且与y轴相交于负半轴．
(以下有(1)、(2)两问，每个考生只须选答一问，若两问都答， 则只以第(2)问计分)
第(1)问：给出四个结论：
①a>0；② b>0；③c>0；④ a+b+c=0．其中正确结论的序号是 （答对得3分，少选、错选均不得分）．
第(2)问：给出四个结论：
① abc<0；②2a+b>0；③a+c=1；④a>1．其中正确结论的序号是 （答对得5分，少选、错选均不得分）．
仔细想一想：①④② ③ ④1这节课你有哪些体会？1.a,b,c等符号与二次函数y=ax2+bx+c有密切的联系；
2.解决这类问题的关键是运用数形结合思想，即会观察图象；如遇到2a+b,2a-b要与对称轴联系等；
3.要注意灵活运用数学知识，具体问题具体分析……112.若关于x的函数y=(a-2)x2-(2a-1)x+a的图象与坐标轴有两个交点，则a可取的值为 ；1.如图是二次函数y1=ax2+bx+c和一次函数y2=mx+n的图象，观察图象写出y2 ≥y1时，x的取值范围是________;课外作业：3.(03武汉)已知抛物线y=ax2+bx+c （a＜0)经过点（－1，0），且满足4a＋2b＋c＞0．以下结论：①a＋b＞0；②a＋c＞0；③－a＋b＋c＞0；④b2-2ac>5a2．其中正确的个数有（ ）（A）1个 （B）2个 （C）3个 （D）4个