求二次函数的关系式
图片预览





文档简介
课件20张PPT。二次函数的
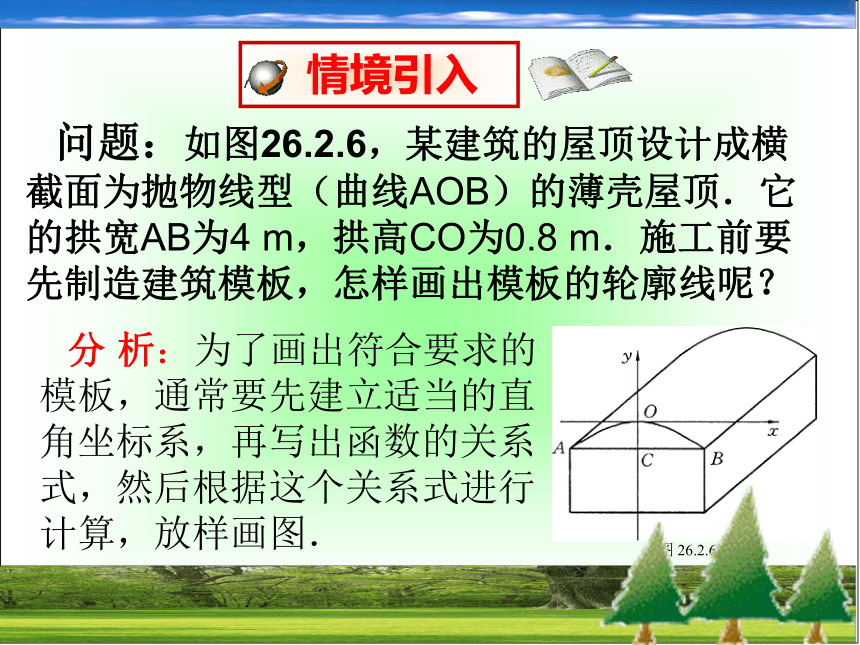
图象和性质一般地,函数关系式中几个独立的系数,那么就需要有相同个数的独立条件都能求出函数关系式。例如:我们在确定一次函数y=kx+b(k≠0)的关系式时,通常需要两个独立的条件;确定反比例函数y=k/x(k ≠0)的关系式时,通常只需要一个条件;如果要确定二次函数y=ax2+bx+c(a ≠0)的关系式时,又需要几个条件呢?问题:如图26.2.6,某建筑的屋顶设计成横截面为抛物线型(曲线AOB)的薄壳屋顶.它的拱宽AB为4 m,拱高CO为0.8 m.施工前要先制造建筑模板,怎样画出模板的轮廓线呢?分 析:为了画出符合要求的模板,通常要先建立适当的直角坐标系,再写出函数的关系式,然后根据这个关系式进行计算,放样画图.如图26.2.6,以AB的垂直平分线为y轴,以过点O的y轴的垂线为x轴,建立直角坐标系.这时,屋顶的横截面所成抛物线的顶点在原点,对称轴是y轴,开口向下,所以可设它的函数关系式为y=ax2 (a<0)(1)又CO=0.8 m,所以点B的坐标为(2,-0.8).因为点B在抛物线上,将它的坐标代入(1),得 -0.8=a ×22,
所以 a=-0.2.
因此,函数关系式是
y=-0.2x2.温馨提示:根据这个关系式,容易画出模板的轮廓线.
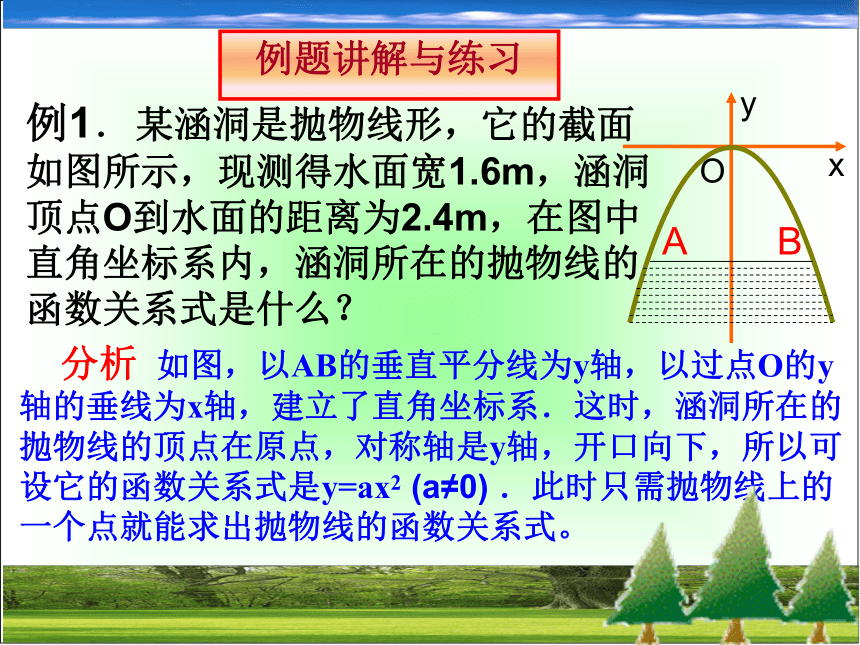
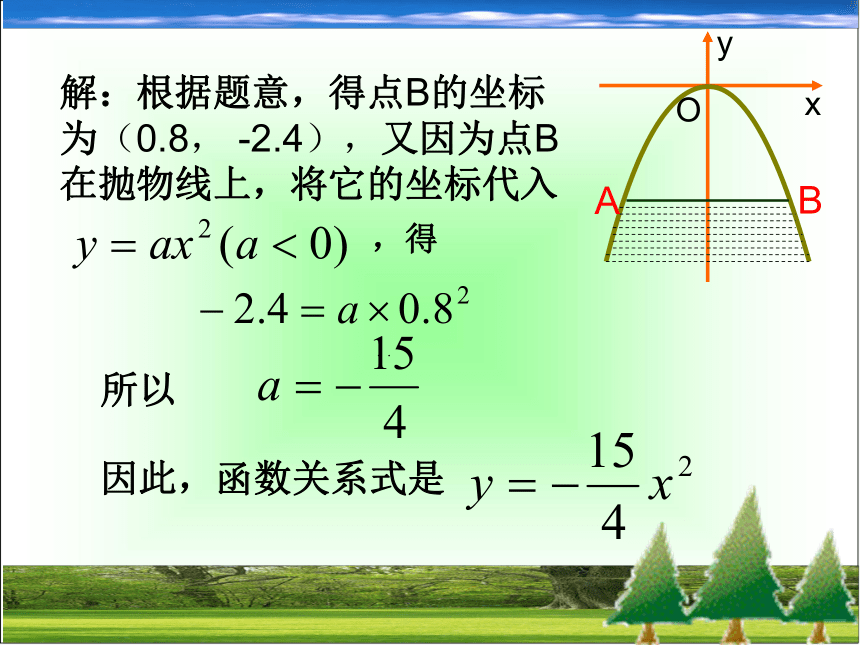
在解决一些实际问题时,往往需要根据某些条件求出函数的关系式. 例题讲解与练习例1.某涵洞是抛物线形,它的截面如图所示,现测得水面宽1.6m,涵洞顶点O到水面的距离为2.4m,在图中直角坐标系内,涵洞所在的抛物线的函数关系式是什么? 分析 如图,以AB的垂直平分线为y轴,以过点O的y轴的垂线为x轴,建立了直角坐标系.这时,涵洞所在的抛物线的顶点在原点,对称轴是y轴,开口向下,所以可设它的函数关系式是y=ax2 (a≠0) .此时只需抛物线上的一个点就能求出抛物线的函数关系式。AB解:根据题意,得点B的坐标为(0.8, -2.4),又因为点B在抛物线上,将它的坐标代入 AB,得所以 .因此,函数关系式是.例2.根据下列条件,分别求出对应的二次函数的关系式.
(1)已知二次函数的图象经过点A(0,-1)、B(1,0)、C(-1,2);
(2)已知抛物线的顶点为(1,-3),且与y轴交于点(0,1);
(3)已知抛物线与x轴交于点M(-3,0)、(5,0),且与y轴交于点(0,-3);
(4)已知抛物线的顶点为(3,-2),且与x轴两交点间的距离为4.例题讲解与练习 分析 (1)根据二次函数的图象经过三个已知点,可设函数关系式为y=ax2+bx+c的形式;(2)根据已知抛物线的顶点坐标,可设函数关系式为y=a(x-1)2-3,再根据抛物线与y轴的交点可求出a的值;(3)根据抛物线与x轴的两个交点的坐标,可设函数关系式为y=a(x+3)(x-5) ,再根据抛物线与y轴的交点可求出a的值;(4)根据已知抛物线的顶点坐标(3,-2),可设函数关系式为y=a(x-3)2-2 ;同时可知抛物线的对称轴为x=3,再由与x轴两交点间的距离为4,可得抛物线与x轴的两个交点为(1,0)和(5,0),任选一个代入 y=a(x-3)2-2 ,即可求出a的值。根据下列条件,分别求出对应的二次函数的关系式.
(1)已知二次函数的图象经过点(0,2)、(1,1)、(3,5);
(2)已知抛物线的顶点为(-1,2),且过点(2,1);
(3)已知抛物线与x轴交于点M(-1,0)、(2,0),且经过点(1,2). 确定二此函数的关系式的一般方法是待定系数法,在选择把二次函数的关系式设成什么形式时,可根据题目中的条件灵活选择,以简单为原则.二次函数的关系式可设如下三种形式: (1)一般式:y=ax2+bx+c(a≠0) ,给出三点坐标可利用此式来求.
(2)顶点式:y=a(x-h)2+k(a≠ 0) ,给出两点,且其中一点为顶点时可利用此式来求.1、已知一个二次函数的图象过点(0,1),它的顶点坐标是(8,9),求这个二次函数的关系式.分析 因为这个二次函数的图象的顶点是(8,9),因此,可以设函数关系式为
y=a(x-8)2 +9.
根据它的图象过点(0,1),容易确定a的值.例题讲解与练习2、已知二次函数的图象过(0,1)、(2,4)、(3,10)三点,求这个二次函数的关系式.解这个方程组,得所以,所求二次函数关系式是 解 设所求二次函数为y=ax2+bx+c,由已知,这个函数的图象过(0,1),可以得到c=1.又由于其图象过(2,4)、(3,10)两点,可以得到 1. 根据下列条件,分别求出对应的二次函数的关系式.
①已知抛物线的顶点在原点,且过点(2,8);
②已知抛物线的顶点是(-1,-2),且过点(1,10);
③已知抛物线过三点:(0,-2)、(1,0)、(2,3). 2. 已知抛物线y=ax2+bx+c过三点:(-1,-1)、(0,-2)、(1,1).
①求这条抛物线所对应的二次函数的关系式;
②写出它的开口方向、对称轴和顶点坐标;
这个函数有最大值还是最小值?这个值是多少? 4. 根据下列条件,分别求出对应的二次函数的关系式.
(1)已知抛物线的顶点在原点,且过点(3,-27);
(2)已知抛物线的顶点在(1,-2),且过点(2,3);
(3)已知抛物线过三点:(-1,2),(0,1),(2,-7).26.2习题第四、五题5. 有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为4 m,跨度为10 m.如图所示,把它的图形放在直角坐标系中.
(1)、求这条抛物线所对应的函数关系式;
(2)、如图,在对称轴右边1 m处,桥洞离水面的高是多少? 用6 m长的铝合金型材做一个形状如图26.2.5所示的矩形窗框.应做成长、宽各为多少时,才能使做成的窗框的透光面积最大?最大透光面积是多少?所以应做成宽1 m、长1.5 m的矩形窗框,才能使透光面积最大.最大面积是1.5 m2.解 设做成的窗框的宽为x m,则长为结束寄语生活是数学的源泉.再见探索是数学的生命线.
图象和性质一般地,函数关系式中几个独立的系数,那么就需要有相同个数的独立条件都能求出函数关系式。例如:我们在确定一次函数y=kx+b(k≠0)的关系式时,通常需要两个独立的条件;确定反比例函数y=k/x(k ≠0)的关系式时,通常只需要一个条件;如果要确定二次函数y=ax2+bx+c(a ≠0)的关系式时,又需要几个条件呢?问题:如图26.2.6,某建筑的屋顶设计成横截面为抛物线型(曲线AOB)的薄壳屋顶.它的拱宽AB为4 m,拱高CO为0.8 m.施工前要先制造建筑模板,怎样画出模板的轮廓线呢?分 析:为了画出符合要求的模板,通常要先建立适当的直角坐标系,再写出函数的关系式,然后根据这个关系式进行计算,放样画图.如图26.2.6,以AB的垂直平分线为y轴,以过点O的y轴的垂线为x轴,建立直角坐标系.这时,屋顶的横截面所成抛物线的顶点在原点,对称轴是y轴,开口向下,所以可设它的函数关系式为y=ax2 (a<0)(1)又CO=0.8 m,所以点B的坐标为(2,-0.8).因为点B在抛物线上,将它的坐标代入(1),得 -0.8=a ×22,
所以 a=-0.2.
因此,函数关系式是
y=-0.2x2.温馨提示:根据这个关系式,容易画出模板的轮廓线.
在解决一些实际问题时,往往需要根据某些条件求出函数的关系式. 例题讲解与练习例1.某涵洞是抛物线形,它的截面如图所示,现测得水面宽1.6m,涵洞顶点O到水面的距离为2.4m,在图中直角坐标系内,涵洞所在的抛物线的函数关系式是什么? 分析 如图,以AB的垂直平分线为y轴,以过点O的y轴的垂线为x轴,建立了直角坐标系.这时,涵洞所在的抛物线的顶点在原点,对称轴是y轴,开口向下,所以可设它的函数关系式是y=ax2 (a≠0) .此时只需抛物线上的一个点就能求出抛物线的函数关系式。AB解:根据题意,得点B的坐标为(0.8, -2.4),又因为点B在抛物线上,将它的坐标代入 AB,得所以 .因此,函数关系式是.例2.根据下列条件,分别求出对应的二次函数的关系式.
(1)已知二次函数的图象经过点A(0,-1)、B(1,0)、C(-1,2);
(2)已知抛物线的顶点为(1,-3),且与y轴交于点(0,1);
(3)已知抛物线与x轴交于点M(-3,0)、(5,0),且与y轴交于点(0,-3);
(4)已知抛物线的顶点为(3,-2),且与x轴两交点间的距离为4.例题讲解与练习 分析 (1)根据二次函数的图象经过三个已知点,可设函数关系式为y=ax2+bx+c的形式;(2)根据已知抛物线的顶点坐标,可设函数关系式为y=a(x-1)2-3,再根据抛物线与y轴的交点可求出a的值;(3)根据抛物线与x轴的两个交点的坐标,可设函数关系式为y=a(x+3)(x-5) ,再根据抛物线与y轴的交点可求出a的值;(4)根据已知抛物线的顶点坐标(3,-2),可设函数关系式为y=a(x-3)2-2 ;同时可知抛物线的对称轴为x=3,再由与x轴两交点间的距离为4,可得抛物线与x轴的两个交点为(1,0)和(5,0),任选一个代入 y=a(x-3)2-2 ,即可求出a的值。根据下列条件,分别求出对应的二次函数的关系式.
(1)已知二次函数的图象经过点(0,2)、(1,1)、(3,5);
(2)已知抛物线的顶点为(-1,2),且过点(2,1);
(3)已知抛物线与x轴交于点M(-1,0)、(2,0),且经过点(1,2). 确定二此函数的关系式的一般方法是待定系数法,在选择把二次函数的关系式设成什么形式时,可根据题目中的条件灵活选择,以简单为原则.二次函数的关系式可设如下三种形式: (1)一般式:y=ax2+bx+c(a≠0) ,给出三点坐标可利用此式来求.
(2)顶点式:y=a(x-h)2+k(a≠ 0) ,给出两点,且其中一点为顶点时可利用此式来求.1、已知一个二次函数的图象过点(0,1),它的顶点坐标是(8,9),求这个二次函数的关系式.分析 因为这个二次函数的图象的顶点是(8,9),因此,可以设函数关系式为
y=a(x-8)2 +9.
根据它的图象过点(0,1),容易确定a的值.例题讲解与练习2、已知二次函数的图象过(0,1)、(2,4)、(3,10)三点,求这个二次函数的关系式.解这个方程组,得所以,所求二次函数关系式是 解 设所求二次函数为y=ax2+bx+c,由已知,这个函数的图象过(0,1),可以得到c=1.又由于其图象过(2,4)、(3,10)两点,可以得到 1. 根据下列条件,分别求出对应的二次函数的关系式.
①已知抛物线的顶点在原点,且过点(2,8);
②已知抛物线的顶点是(-1,-2),且过点(1,10);
③已知抛物线过三点:(0,-2)、(1,0)、(2,3). 2. 已知抛物线y=ax2+bx+c过三点:(-1,-1)、(0,-2)、(1,1).
①求这条抛物线所对应的二次函数的关系式;
②写出它的开口方向、对称轴和顶点坐标;
这个函数有最大值还是最小值?这个值是多少? 4. 根据下列条件,分别求出对应的二次函数的关系式.
(1)已知抛物线的顶点在原点,且过点(3,-27);
(2)已知抛物线的顶点在(1,-2),且过点(2,3);
(3)已知抛物线过三点:(-1,2),(0,1),(2,-7).26.2习题第四、五题5. 有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为4 m,跨度为10 m.如图所示,把它的图形放在直角坐标系中.
(1)、求这条抛物线所对应的函数关系式;
(2)、如图,在对称轴右边1 m处,桥洞离水面的高是多少? 用6 m长的铝合金型材做一个形状如图26.2.5所示的矩形窗框.应做成长、宽各为多少时,才能使做成的窗框的透光面积最大?最大透光面积是多少?所以应做成宽1 m、长1.5 m的矩形窗框,才能使透光面积最大.最大面积是1.5 m2.解 设做成的窗框的宽为x m,则长为结束寄语生活是数学的源泉.再见探索是数学的生命线.
