二次函数的应用[下学期]

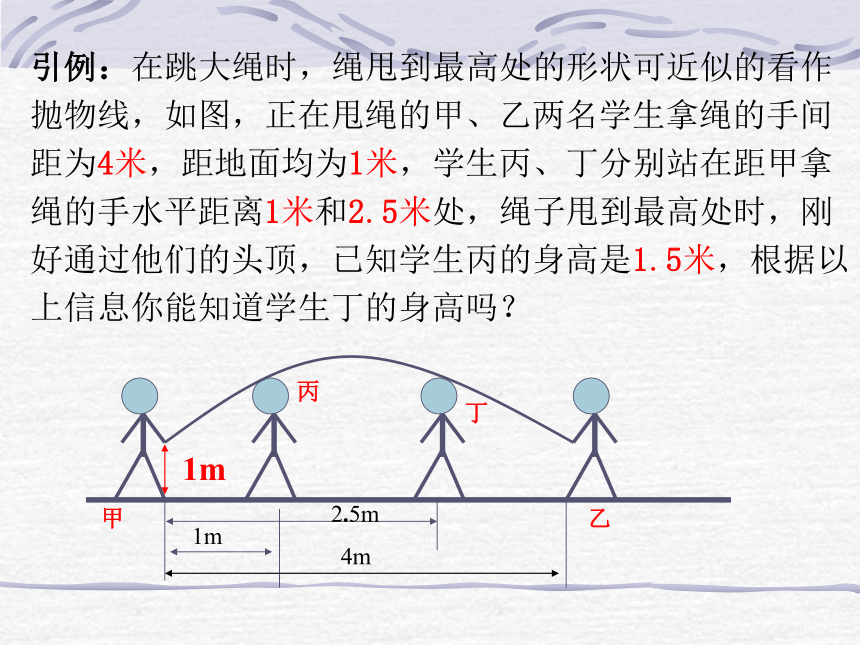
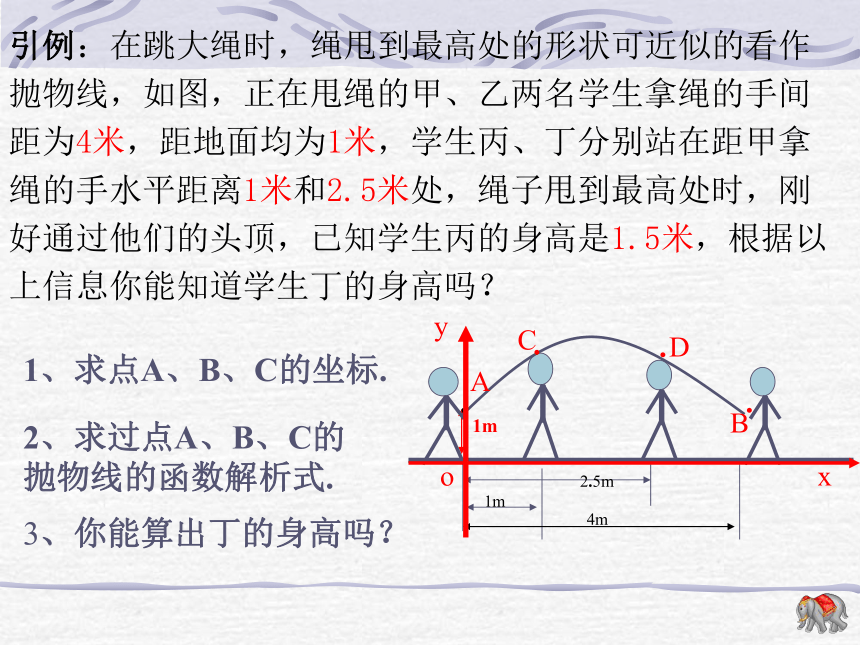
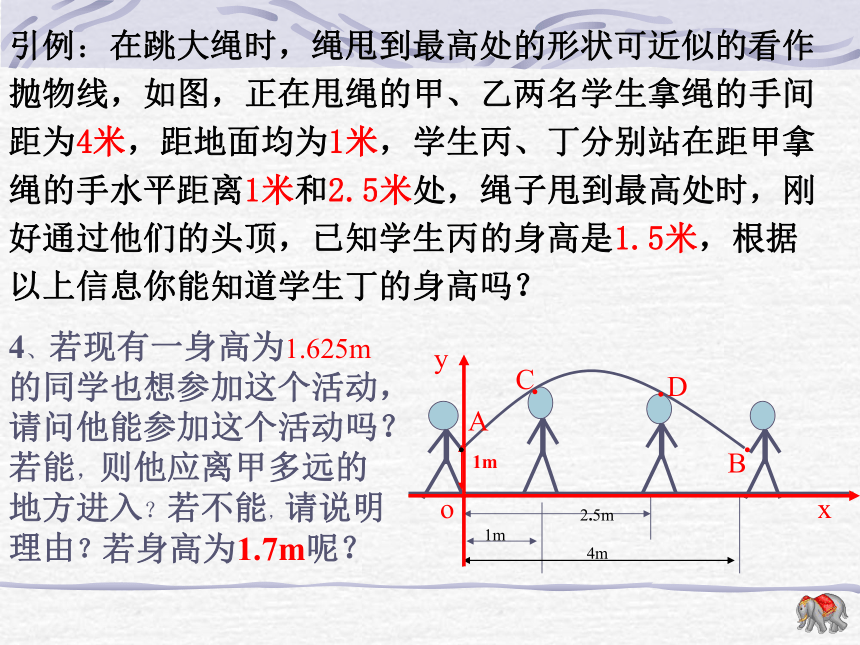
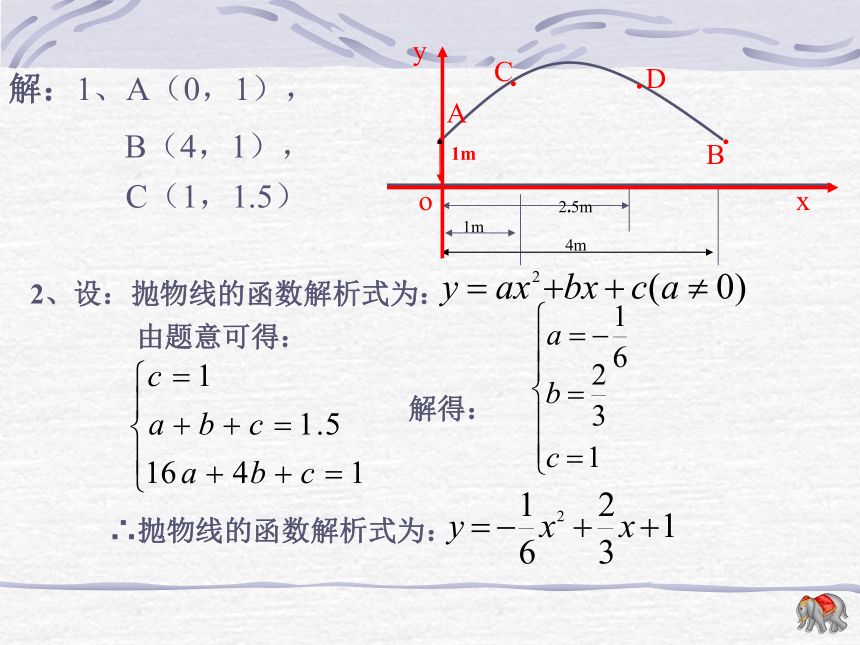
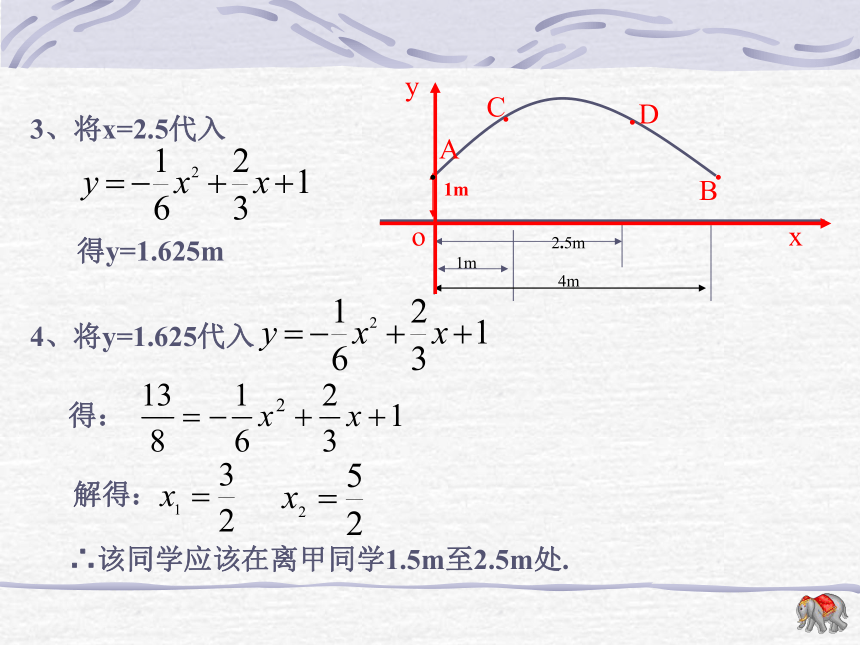
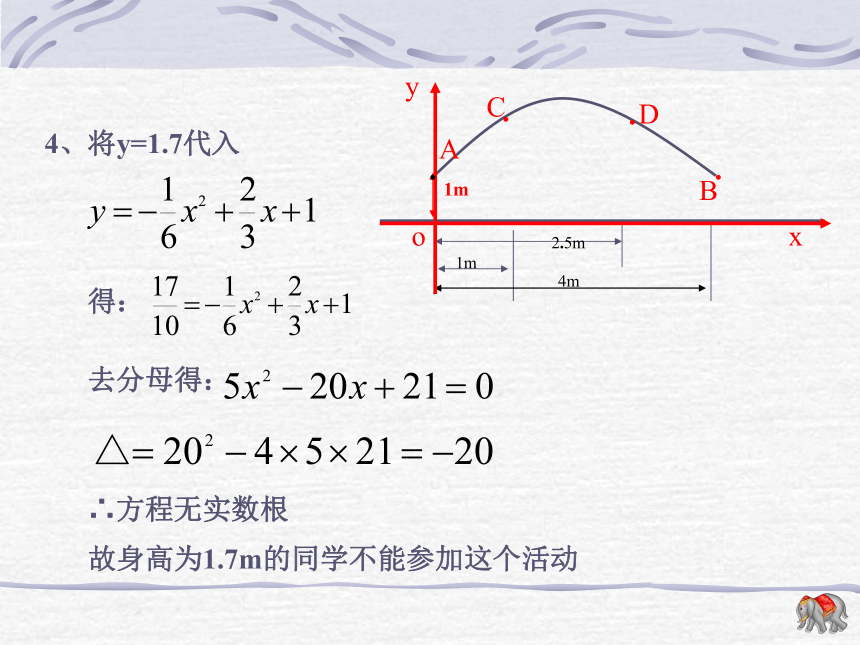
课件22张PPT。二次函数的应用虹星桥镇中学周小方引例：在跳大绳时，绳甩到最高处的形状可近似的看作抛物线，如图，正在甩绳的甲、乙两名学生拿绳的手间距为4米，距地面均为1米，学生丙、丁分别站在距甲拿绳的手水平距离1米和2.5米处，绳子甩到最高处时，刚好通过他们的头顶，已知学生丙的身高是1.5米，根据以上信息你能知道学生丁的身高吗？二次函数的应用121或－15、已知如图A（1，1），AB=3，AB∥x轴OxyAB则点B的坐标为__________.（4，1）引例：在跳大绳时，绳甩到最高处的形状可近似的看作抛物线，如图，正在甩绳的甲、乙两名学生拿绳的手间距为4米，距地面均为1米，学生丙、丁分别站在距甲拿绳的手水平距离1米和2.5米处，绳子甩到最高处时，刚好通过他们的头顶，已知学生丙的身高是1.5米，根据以上信息你能知道学生丁的身高吗？1、求点A、B、C的坐标.2、求过点A、B、C的抛物线的函数解析式.3、你能算出丁的身高吗？引例：在跳大绳时，绳甩到最高处的形状可近似的看作抛物线，如图，正在甩绳的甲、乙两名学生拿绳的手间距为4米，距地面均为1米，学生丙、丁分别站在距甲拿绳的手水平距离1米和2.5米处，绳子甩到最高处时，刚好通过他们的头顶，已知学生丙的身高是1.5米，根据以上信息你能知道学生丁的身高吗？4、若现有一身高为1.625m的同学也想参加这个活动，请问他能参加这个活动吗？若能，则他应离甲多远的地方进入？若不能，请说明理由？若身高为1.7m呢？2、设：抛物线的函数解析式为：由题意可得：解得：∴抛物线的函数解析式为：∴该同学应该在离甲同学1.5m至2.5m处.·例：有一座抛物线形拱桥，在正常水位时水面A B的宽为20m，如果水位上升3米时，水面CD的宽为10m．（2）求此抛物线的解析式；（3）现有一辆载有救援物质的货车，从甲出发需经此桥开往乙，已知甲距此桥 280km（桥长忽略不计）货车以 40km／h的速度开往乙；当行驶1小时，忽然接到通知，前方连降暴雨，造成水位以每小时0．25m的速度持续上涨（货车接到通知时水位在CD处，当水位到达最高点E时，禁止车辆通行）试问：如果货车按原速行驶，能否安全通过此桥？若能，请说明理由，若不能，要使货车安全通过此桥，速度应不小于每小时多少千米？例：有一座抛物线形拱桥，在正常水位时水面A B的宽为20m，如果水位上升3米时，水面CD的宽为10m．解：（1）B（10，0），D（5，3）（2）设抛物线的函数解析式为由题意可得：解得：∴抛物线的函数解析式为：设货车速度为x km／h，能安全通过此桥.则4x+40≥280 解得x≥60故速度不小于60km／h，货车能安全通过此桥。（4）现有一艘载有救援物质的货船，从甲出发需经此桥开往乙，已知甲距此桥 280km，货船以 40km／h的速度开往乙；当行驶1小时，忽然接到通知，前方连降暴雨，造成水位以每小时0．25m的速度持续上涨（货车接到通知时水位在AB处，当水位到达CD时，禁止船只通行）试问：如果货船按原速行驶，能否安全通过此桥？若能，请说明理由，若不能，要使货船安全通过此桥，速度应不小于每小时多少千米？例：有一座抛物线形拱桥，在正常水位时水面A B的宽为20m，如果水位上升3米时，水面CD的宽为10m．1、如图是我县某公园一圆形喷水池的效果图，水流在各方向沿形状相同的抛物线落下。建立如图坐标系，如果喷头所在处A（0，1.25），水流路线最高处B（1，2.25），则该抛物线的解析式为 __________________。如果不考虑其他因素，那么水池的半径至少要_____________米，才能使喷出的水流不致落到池外。2、如图，在一面靠墙的空地上用长24米的篱笆，围成中间隔有二道篱笆的长方形花圃，设花圃的宽AB为x米，面积为S平方米。
(1)求S与x的函数关系式及自变量的取值范围；
(2)当x取何值时所围成的花圃面积最大，最大值是多少？
*(3)若墙的最大可用长度为8米，则求围成花圃的最大面积。(2)当x＝ 时，S最大值＝ ＝36（平方米）解：小结:1、本节课主要复习了已知横坐标（或纵坐标），
求纵坐标（或横坐标）的方法。2、主要学习了如何将实际问题转化为数学问题，
特别是如何利用二次函数的有关性质解决实际
问题的方法.3、利用二次函数解决实际问题时，建立适当的直
角坐标系，是解决问题的关键。谢谢！二次函数解析式的一般的设法是：1、设函数解析式为：2、设函数解析式为：