第五章 相交线与平行线 第二、三课时垂线
文档属性
| 名称 | 第五章 相交线与平行线 第二、三课时垂线 |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-07-01 00:00:00 | ||
图片预览







文档简介
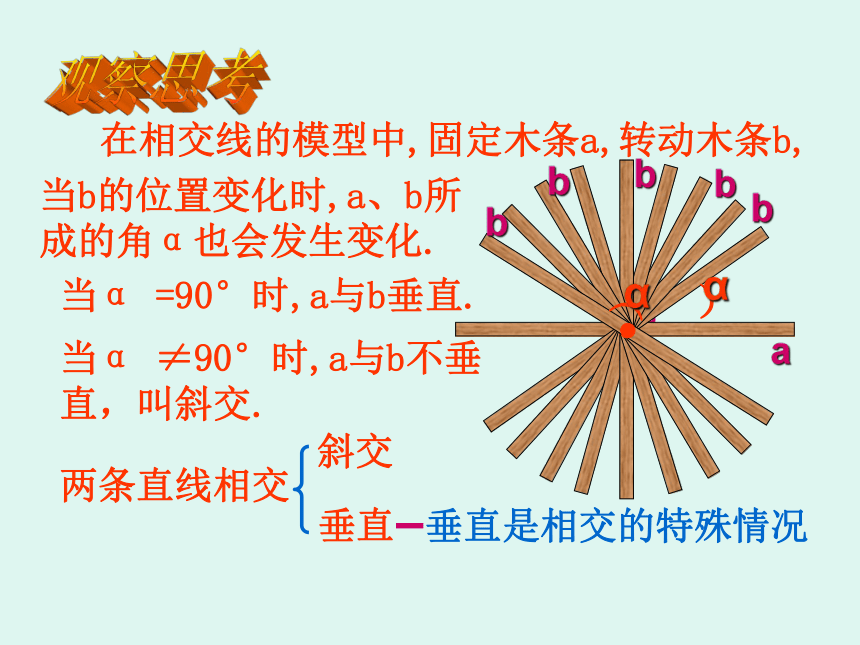
课件44张PPT。七年级(下)数学(人教版)5.1.2垂线在相交线的模型中,固定木条a,转动木条b,当α =90°时,a与b垂直.当b的位置变化时,a、b所成的角α也会发生变化.当α ≠90°时,a与b不垂直,叫斜交.两条直线相交斜交垂直垂直是相交的特殊情况观察思考)α abbbbb)α 1.垂直定义:当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足。例如、如图,a、b互相垂直,O叫垂足.a叫b的垂线,b也叫a的垂线。一、垂直的定义从垂直的定义可知,
判断两条直线互相垂直的关键:
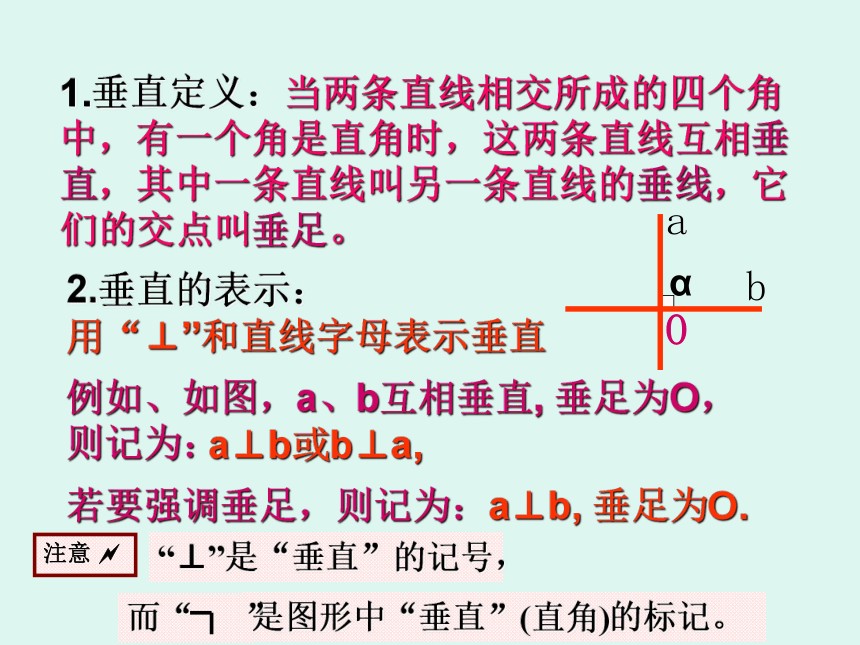
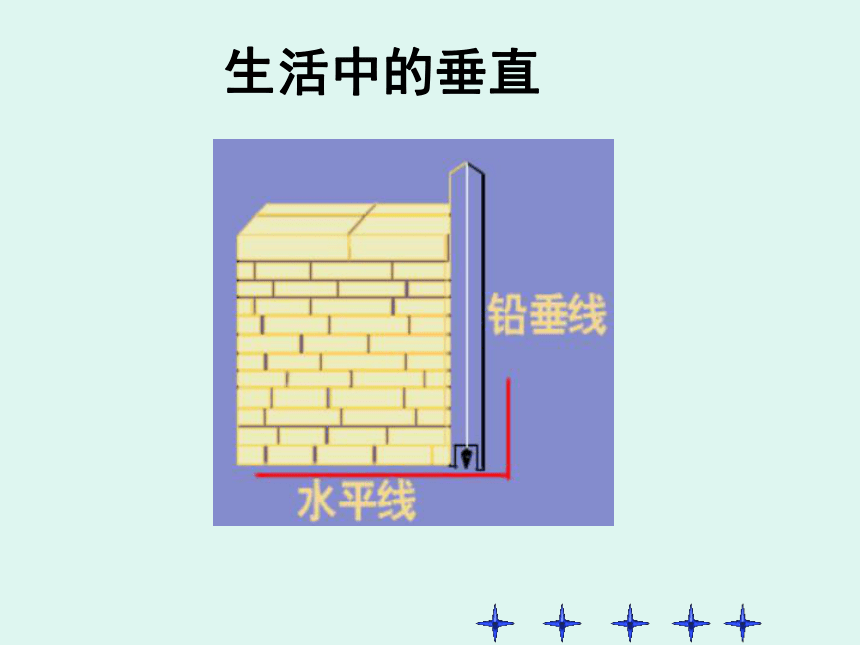
只要找到两条直线相交时四个交角中一个角是直角。1.垂直定义:当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足。ba用“⊥”和直线字母表示垂直Oα 2.垂直的表示:例如、如图,a、b互相垂直, 垂足为O,则记为:a⊥b或b⊥a, 若要强调垂足,则记为:a⊥b, 垂足为O. 日常生活中,两条直线互相垂直的情形很常见,说出图5.1-6中的一些互相垂直的线条.你能再举出其他例子吗?生活中的垂直生活中的垂直生活中的垂直生活中的垂直生活中的垂直生活中的垂直生活中的垂直ABCDO书写形式: 如图,当直线AB与CD相交于O点,∠AOD=90°时,AB⊥CD,垂足为O。∵∠AOD=90°(已知)
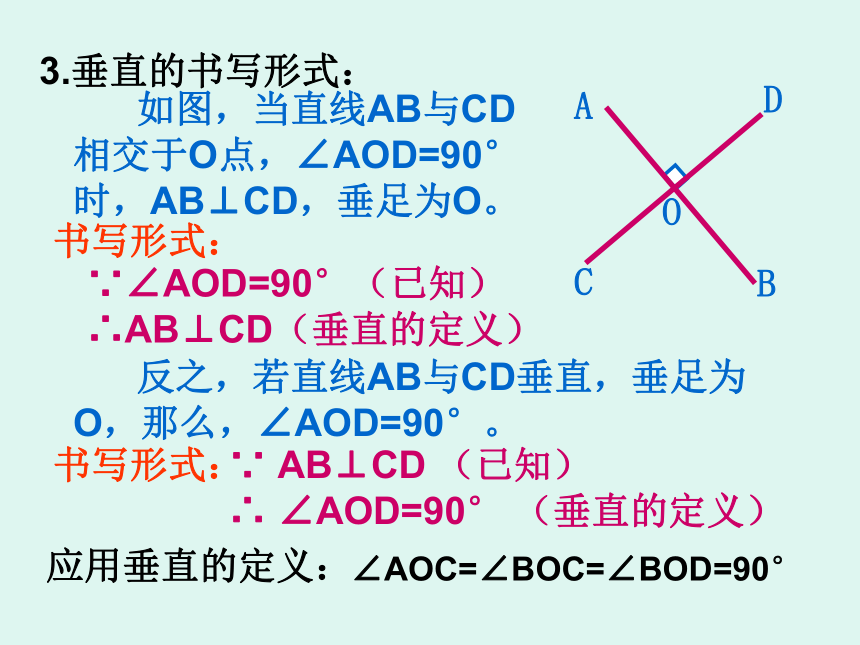
∴AB⊥CD(垂直的定义)书写形式: 反之,若直线AB与CD垂直,垂足为O,那么,∠AOD=90°。3.垂直的书写形式:∵ AB⊥CD (已知)
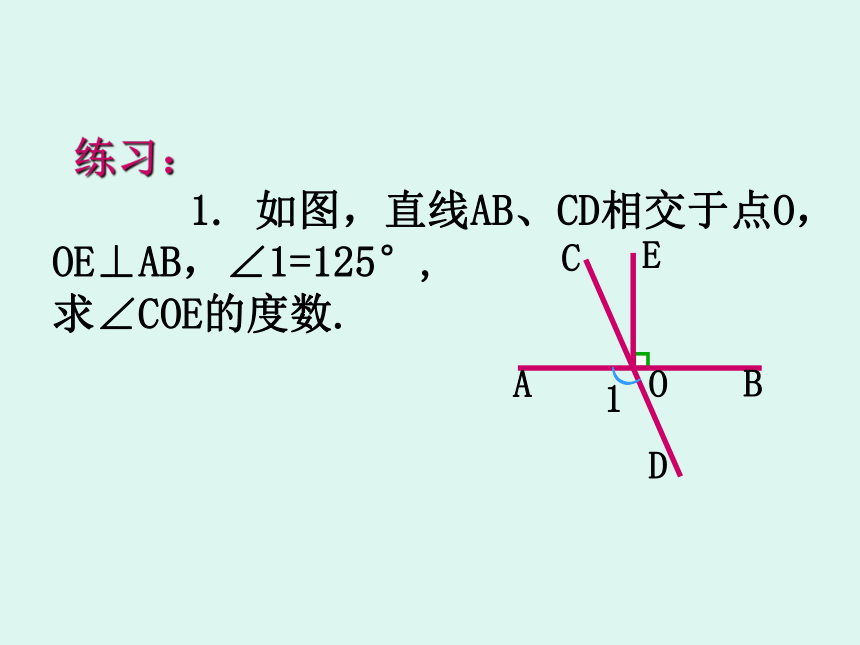
∴ ∠AOD=90° (垂直的定义)应用垂直的定义:∠AOC=∠BOC=∠BOD=90°练习: 1. 如图,直线AB、CD相交于点O,OE⊥AB,∠1=125°,
求∠COE的度数.ACEBDO1)2、如图,∠ABC=90° ,∠1=60° ,过B作AC的垂线BO,垂足是O,过O作BC的垂线,垂足是D,若∠1= ∠2,求∠ABO, ∠BOD.∵BO ⊥AC于O点(已知)∵∠ABC=90°( )∠1=60°( )已知∴∠ABO=30°解:(已知)∴∠BOC=90°∴∠BOD=30°(互余的定义)(互余的定义)已知(垂直的定义)又∵∠2=∠1∴∠2=60°(等量代换)
1.下面四种判断两条直线垂直的方法正确的有___个????????????????? [??? ]
(1)两条直线相交所成的四个角中有一个角是直角,则这两条直线互相垂直.
(2)两条直线相交,有一组邻补角相等,则这两条直线互相垂直.
(3)两条直线相交,所成的四个角相等,这两条直线互相垂直.
(4)两条直线相交,有一组对顶角互补,则这两条直线互相垂直.
A.4????????? B.3???????????? C.2???????????? D.1选择题巩固练习 A2.两条直线相交所成的四个角中,下列条 件中能判定两条直线垂直的是 [??? ]
A.有两个角相等 B.有两对角相等
C.有三个角相等 D.有四对邻补角
3.两个角的平分线相互垂直的有? [??? ]
A.两角互补; B.两角互为对顶角;
C.两角都是直角; D.两角为邻补角
巩固练习 选择题CD看谁做得快1.若直线m、n相交于点O,
∠1=90°,则__________。
2.若直线AB、CD相交于点O,
且AB⊥CD,那么∠BOD=____。
3.如图,BO⊥AO,∠BOC
与∠BOA的度数之比为1:5,
那么∠COA=_____,
∠BOC的补角为______度。m⊥n90°75°165二、垂线的画法问题:
怎么样画垂线?用三角板画两条互相垂直的直线1.垂线的画法:问题:
这样画l的垂线可以画几条?1放、
2靠、
3画线、lO如图,已知直线 l,作l的垂线。工具:直尺、三角板A无数条1.垂线的画法:lA如图,已知直线 l 和l上的一点A ,作l的垂线.B4画线:沿着三角板的另一直角边画出垂线.1放:放直尺,直尺的一边要与已知直线重合;3移:移动三角板到已知点;2靠:靠三角板,把三角板的一直角边靠在直尺上; 则所画直线AB是过点A的直线l的垂线.1.垂线的画法:lA如图,已知直线 l 和l外的一点A ,作l的垂线.B4画线:沿着三角板的另一直角边画出垂线.1放:放直尺,直尺的一边要与已知直线重合;3移:移动三角板到已知点;2靠:靠三角板,把三角板的一直角边靠在直尺上; 则所画直线AB是过点A的直线l的垂线.请同学们画一下 结论:
过一点有且只有一条直线与已知直线垂直.能作一条,而且只能作一条.问题:过已知直线 l 和l上(或外)的一点A ,作l的垂线,可以作几条? 注意:
过一点画已知线段(或射线)的垂线,就是画这条线段(或射线)所在直线的垂线.线段、射线的垂线应怎么画呢? 练习:P7/练习EEE注意:画线段(或射线)的垂线时,有时要将线段延长(或将射线反向延长)后再画垂线. 2、您还能用直尺在方格纸上画出其它互相垂直的两条直线吗?如何在方格纸上画两垂直的直线试讨论一下,有几种画法?若取定A、B 两点怎样再取两点 C、D、才能使CD⊥AB?有什么规律?——横4 竖3,横 3竖4 。课堂练习 C2、如图,分别过A、B、C作BC、AC、AB的垂线。3、如图,过P作直线PM⊥OA,垂足为点M.
过P作线段PN⊥OB于N点。DEFMN解:如图、直线AD⊥BC于D、直线BE⊥AC于E、直线CF⊥AB于F解:如图、直线PM⊥OA于M、线段PN⊥OB于N思考 有人不慎掉入有鳄鱼的湖中。如图,他在P点,应选择什么样的路线尽快游到岸边m呢?连接直线外一点与直线上各点的所有线段中,垂线段最短。垂线段最短直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。垂线段的长度简单说成:垂线段最短.1、已知点A,与点A的距离是5cm的线段可画( )
A. 1条 B. 2条 C. 3条 D. 无数条D选择题:B如图,怎样测量 点A 到 直线m 的距离?m1.过点A画出直线m的垂线AB,垂足为B;2.用直尺量出垂线段AB的长.AB 例1、如图,量出(1)村庄A与货场B的距离,(2)货场B到铁道的距离。例2、如图, 1)画出线段BC的中点M,连结AM; 2)比较点B与点C到直线AM的距离。ABCPQ∴BP=CQ例3、如图,点M、N分别在直线AB、CD上,用三角板画图, 1)过M点画CD的垂线交CD于F点, 2)M点和N点的距离是线段____的长, 3)M点到CD的距离是线段____的长。MNMFABCDMN∴直线MF为所求垂线。??? 例4、如图2-23,试用直尺或三角板量出:
1.城市A与城市B的距离.
2.城市A,B到大河l的距离. 如图:在铁路旁边有一张庄,现在要建一火车站,为了使张庄人乘火车最方便(即距离最近),请你在铁路上选一点来建火车站,并说明理由。张庄拓展应用1垂线段最短拓 展 应 用2 如图:要把水渠中的水引到水池C中,在渠岸的什么地方开沟,水沟的长度才能最短?
请画出图来,并说明理由。C∟垂线段最短立定跳远中,体育老师是如何测量运动员的成绩的?体育老师实际上测量的是点到直线的距离
小常识ABCDEFGM· · 问题1:长方体的顶点A处有一只蚂蚁想爬到点C处,请你帮它画出爬行的最佳路线。并说明理由。 问题2:若A处的蚂蚁想爬到棱BC上,你认为它的最佳路线是什么? 问题3:若蚂蚁在点M处,想爬到棱BC上,请你设计一条最佳路线。┏
N你会设计吗? 在直角三角形的三条边中哪一条最长?思考答:直角所对的边即斜边最长.选择题:2.如图, AC⊥BC, ∠C=900 ,线段AC、BC、CD中最短的是( )
(A) AC (B) BC (C) CD (D) 不能确定DABCC想一想:DBCAE已知: 如图AD<AE <AC<AB 能说AD的长是A到BC的 距离吗?答:不能。?? 例2:如图2-22,AC⊥BC于C,CD⊥AB于D,DE⊥BC于E.试比较四条线段AC,CD,DE和AB的大小解:∵ AC⊥BC于C,(已知)
∴ AC<AB.(垂线的性质二)
又∵ CD⊥AD于D,(已知)
∴ CD<AC.(垂线的性质二)
∵ DE⊥CE于E,(已知)
∴ DE<CD.(垂线的性质二)
∴ AB>AC>CD>DE.回忆两条直线相交这部分知识,并问:你们能够把它们画成一个知识结构图吗? 小结
判断两条直线互相垂直的关键:
只要找到两条直线相交时四个交角中一个角是直角。1.垂直定义:当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足。ba用“⊥”和直线字母表示垂直Oα 2.垂直的表示:例如、如图,a、b互相垂直, 垂足为O,则记为:a⊥b或b⊥a, 若要强调垂足,则记为:a⊥b, 垂足为O. 日常生活中,两条直线互相垂直的情形很常见,说出图5.1-6中的一些互相垂直的线条.你能再举出其他例子吗?生活中的垂直生活中的垂直生活中的垂直生活中的垂直生活中的垂直生活中的垂直生活中的垂直ABCDO书写形式: 如图,当直线AB与CD相交于O点,∠AOD=90°时,AB⊥CD,垂足为O。∵∠AOD=90°(已知)
∴AB⊥CD(垂直的定义)书写形式: 反之,若直线AB与CD垂直,垂足为O,那么,∠AOD=90°。3.垂直的书写形式:∵ AB⊥CD (已知)
∴ ∠AOD=90° (垂直的定义)应用垂直的定义:∠AOC=∠BOC=∠BOD=90°练习: 1. 如图,直线AB、CD相交于点O,OE⊥AB,∠1=125°,
求∠COE的度数.ACEBDO1)2、如图,∠ABC=90° ,∠1=60° ,过B作AC的垂线BO,垂足是O,过O作BC的垂线,垂足是D,若∠1= ∠2,求∠ABO, ∠BOD.∵BO ⊥AC于O点(已知)∵∠ABC=90°( )∠1=60°( )已知∴∠ABO=30°解:(已知)∴∠BOC=90°∴∠BOD=30°(互余的定义)(互余的定义)已知(垂直的定义)又∵∠2=∠1∴∠2=60°(等量代换)
1.下面四种判断两条直线垂直的方法正确的有___个????????????????? [??? ]
(1)两条直线相交所成的四个角中有一个角是直角,则这两条直线互相垂直.
(2)两条直线相交,有一组邻补角相等,则这两条直线互相垂直.
(3)两条直线相交,所成的四个角相等,这两条直线互相垂直.
(4)两条直线相交,有一组对顶角互补,则这两条直线互相垂直.
A.4????????? B.3???????????? C.2???????????? D.1选择题巩固练习 A2.两条直线相交所成的四个角中,下列条 件中能判定两条直线垂直的是 [??? ]
A.有两个角相等 B.有两对角相等
C.有三个角相等 D.有四对邻补角
3.两个角的平分线相互垂直的有? [??? ]
A.两角互补; B.两角互为对顶角;
C.两角都是直角; D.两角为邻补角
巩固练习 选择题CD看谁做得快1.若直线m、n相交于点O,
∠1=90°,则__________。
2.若直线AB、CD相交于点O,
且AB⊥CD,那么∠BOD=____。
3.如图,BO⊥AO,∠BOC
与∠BOA的度数之比为1:5,
那么∠COA=_____,
∠BOC的补角为______度。m⊥n90°75°165二、垂线的画法问题:
怎么样画垂线?用三角板画两条互相垂直的直线1.垂线的画法:问题:
这样画l的垂线可以画几条?1放、
2靠、
3画线、lO如图,已知直线 l,作l的垂线。工具:直尺、三角板A无数条1.垂线的画法:lA如图,已知直线 l 和l上的一点A ,作l的垂线.B4画线:沿着三角板的另一直角边画出垂线.1放:放直尺,直尺的一边要与已知直线重合;3移:移动三角板到已知点;2靠:靠三角板,把三角板的一直角边靠在直尺上; 则所画直线AB是过点A的直线l的垂线.1.垂线的画法:lA如图,已知直线 l 和l外的一点A ,作l的垂线.B4画线:沿着三角板的另一直角边画出垂线.1放:放直尺,直尺的一边要与已知直线重合;3移:移动三角板到已知点;2靠:靠三角板,把三角板的一直角边靠在直尺上; 则所画直线AB是过点A的直线l的垂线.请同学们画一下 结论:
过一点有且只有一条直线与已知直线垂直.能作一条,而且只能作一条.问题:过已知直线 l 和l上(或外)的一点A ,作l的垂线,可以作几条? 注意:
过一点画已知线段(或射线)的垂线,就是画这条线段(或射线)所在直线的垂线.线段、射线的垂线应怎么画呢? 练习:P7/练习EEE注意:画线段(或射线)的垂线时,有时要将线段延长(或将射线反向延长)后再画垂线. 2、您还能用直尺在方格纸上画出其它互相垂直的两条直线吗?如何在方格纸上画两垂直的直线试讨论一下,有几种画法?若取定A、B 两点怎样再取两点 C、D、才能使CD⊥AB?有什么规律?——横4 竖3,横 3竖4 。课堂练习 C2、如图,分别过A、B、C作BC、AC、AB的垂线。3、如图,过P作直线PM⊥OA,垂足为点M.
过P作线段PN⊥OB于N点。DEFMN解:如图、直线AD⊥BC于D、直线BE⊥AC于E、直线CF⊥AB于F解:如图、直线PM⊥OA于M、线段PN⊥OB于N思考 有人不慎掉入有鳄鱼的湖中。如图,他在P点,应选择什么样的路线尽快游到岸边m呢?连接直线外一点与直线上各点的所有线段中,垂线段最短。垂线段最短直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。垂线段的长度简单说成:垂线段最短.1、已知点A,与点A的距离是5cm的线段可画( )
A. 1条 B. 2条 C. 3条 D. 无数条D选择题:B如图,怎样测量 点A 到 直线m 的距离?m1.过点A画出直线m的垂线AB,垂足为B;2.用直尺量出垂线段AB的长.AB 例1、如图,量出(1)村庄A与货场B的距离,(2)货场B到铁道的距离。例2、如图, 1)画出线段BC的中点M,连结AM; 2)比较点B与点C到直线AM的距离。ABCPQ∴BP=CQ例3、如图,点M、N分别在直线AB、CD上,用三角板画图, 1)过M点画CD的垂线交CD于F点, 2)M点和N点的距离是线段____的长, 3)M点到CD的距离是线段____的长。MNMFABCDMN∴直线MF为所求垂线。??? 例4、如图2-23,试用直尺或三角板量出:
1.城市A与城市B的距离.
2.城市A,B到大河l的距离. 如图:在铁路旁边有一张庄,现在要建一火车站,为了使张庄人乘火车最方便(即距离最近),请你在铁路上选一点来建火车站,并说明理由。张庄拓展应用1垂线段最短拓 展 应 用2 如图:要把水渠中的水引到水池C中,在渠岸的什么地方开沟,水沟的长度才能最短?
请画出图来,并说明理由。C∟垂线段最短立定跳远中,体育老师是如何测量运动员的成绩的?体育老师实际上测量的是点到直线的距离
小常识ABCDEFGM· · 问题1:长方体的顶点A处有一只蚂蚁想爬到点C处,请你帮它画出爬行的最佳路线。并说明理由。 问题2:若A处的蚂蚁想爬到棱BC上,你认为它的最佳路线是什么? 问题3:若蚂蚁在点M处,想爬到棱BC上,请你设计一条最佳路线。┏
N你会设计吗? 在直角三角形的三条边中哪一条最长?思考答:直角所对的边即斜边最长.选择题:2.如图, AC⊥BC, ∠C=900 ,线段AC、BC、CD中最短的是( )
(A) AC (B) BC (C) CD (D) 不能确定DABCC想一想:DBCAE已知: 如图AD<AE <AC<AB 能说AD的长是A到BC的 距离吗?答:不能。?? 例2:如图2-22,AC⊥BC于C,CD⊥AB于D,DE⊥BC于E.试比较四条线段AC,CD,DE和AB的大小解:∵ AC⊥BC于C,(已知)
∴ AC<AB.(垂线的性质二)
又∵ CD⊥AD于D,(已知)
∴ CD<AC.(垂线的性质二)
∵ DE⊥CE于E,(已知)
∴ DE<CD.(垂线的性质二)
∴ AB>AC>CD>DE.回忆两条直线相交这部分知识,并问:你们能够把它们画成一个知识结构图吗? 小结
